By the rivers of Babylon

The Babylonian civilization of Mesopotamia dates to around 2000 BCE and was located in the region between the two rivers Tigris and Euphrates. Prior to this the Sumerian civilization flourished here from around 3500 BCE. During this civilization cities were built and administration mechanism, legal systems, irrigation channels and even a postal service were developed. The Babylonians invaded Mesopotamia around 2000 BCE and after defeating the Sumerians established their capital at Babylon around 1900 BCE.

This Sumerian civilization introduced writing and also had a method of counting, which was subsequently further developed by the Babylonians. The cuneiform script was used to inscribe on wet clay, which was baked in the sun (incidentally the cuneiform fonts for L^ATEX are also available nowadays!). This script was deciphered by Sir Henry Creswicke Rawlinson. The famous Code of Hammurabi dates from the Babylonian period and lists out around 280 laws for governance.

From the excavations at the Babylonian sites, many clay tablets with inscriptions have been found. Of these we will discuss some which are connected with mathematics. The number system used by the Babylonians was a positional system with a base of 60. There are various reasons put forth by historians for the use of this sexagesimal system. They had also divided the day into 24 hours, each hour having 60 minutes and each minute having 60 seconds. This sexagesimal system for measurement of time survives even now².

We restrict ourselves to the tablets which are related to the Pythagoras' theorem, in particular the tablets YBC 7289 (from the Yale University collection), Plimpton 322 (from the Columbia University collection), the more recently excavated Susa tablet (discovered at Shoosh, Iran) and Tell Dhibayi tablet (discovered near Baghdad, Iraq). All these tablets are dated between 1900 BCE and 1600 BCE. However, before we proceed further, here is a translation of a problem and its solution inscribed on a Babylonian tablet kept at the British Museum, London.

4 is the length and 5 the diagonal. What is the breadth?
Its size is not known.
4 times 4 is 16,
5 times 5 is 25.
You take 16 from 25 and there remains 9.
What times what shall I take in order to get 9?
3 times 3 is 9,
3 is the breadth.

Of course, it does not need any elucidation that the geometric aspect of the Pythagorean triplet is being discussed here.

For further confirmation of the fact that the Babylonians were quite familiar with the geometry behind Pythagorean triples we look at the tablet YBC 7289.

Figure 1: Diagram on the tablet YBC 7289.

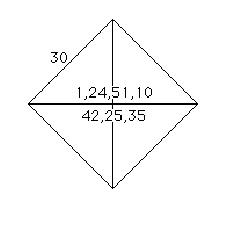
The diagram on this tablet is shown in Figure 1. A note of explanation is needed for this diagram. On one side of the square is inscribed 30, while on the horizontal diagonal are inscribed two numbers 1 24 51 10 and 42 25 35. Recalling that the Babylonians had a sexagesimal system³ and assuming that the space between the digits represent position values of the (sexagesimal) digits and also assuming that the first number is $1.\bar{24}~ \bar{51}~ \bar{10}~(\mbox{mod } 60)$ and the second number is $\bar{42}.\bar{25}~ \bar{35}~\bar{42}~\bar{25}~\bar{35}~(\mbox{mod } 60)$, then translating these numbers gives $1.\bar{24}~ \bar{51}~ \bar{10}~(\mbox{mod } 60) = 1.41421296~ (\mbox{mod } 10)$ and $\bar{42}.\bar{25}~ \bar{35}~\bar{42}~\bar{25}~\bar{35}~(\mbox{mod } 60)= 42.4263888~(\mbox{mod } 10) = 30 \times 1.41421296~(\mbox{mod } 10)$. Note that $\sqrt{\mbox{2}} \approx 1.41421356~(\mbox{mod } 10)$.

Although this confirms that the Babylonians were familiar with the geometry behind Pythagorean triplets, it raises the question as to how did they compute $\sqrt{2}$ so accurately.

Two among the many possibilities postulated are (i) the Babylonians were familiar with the Heron's method and (ii) they used an algorithmic method based on calculating squares. Heron's method is as follows:- take a guess $x$ for $\sqrt{2}$ and let $y = x^2 -2$ denote the error. Now consider $(x-\frac{y}{2x})^2 = x^2 - y + (\frac{y}{2x})^2 = 2 + (\frac{y}{2x})^2$; for small $y$, $(\frac{y}{2x})^2$ is even smaller, thus $(x-\frac{y}{2x})^2$ is a better approximation of $2$. By this method, staring with $x = 1$ in only two steps one obtains the approximation $1.\bar{24}~ \bar{51}~ \bar{10}~(\mbox{mod } 10)$. The algorithmic method is as follows:- take two guesses $x$ and $y$, one larger and the other smaller than $\sqrt{2}$; if the number $(\frac{x+y}{2})^2$ is larger (respectively, smaller) than $2$ then iterate the process with $\frac{x+y}{2}$ and $\min\{x,y\}$ (respectively, $\max\{x,y\}$ instead of the original guesses $x$ and $y$ - continue till the desired accuracy. By this method, taking $x = 1$ and $y = 2$, one obtains the approximation $1.\bar{24}~ \bar{51}~ \bar{10}$ for $\sqrt{2}$ in 19 steps⁴.

The Plimpton 322 tablet contains an array of numbers (sexagesimal) divided into 15 rows and 4 columns. The last column just gives the row numbers, while the numbers in the first three columns are very interesting. Taking $a$, $b$ and $c$ to be the numbers in the first, second and third columns respectively, we see that they satisfy the relation $a = \frac{c^2}{c^2-b^2}$ and that $c^2 - b^2$ is a perfect square⁵. While some historians postulate a relation between the secant function and the first column, the mathematician Zeeman observes that taking $b = m^2 - n^2$, $h = 2mn$ and $c = m^2 +n^2$ to construct the Pythagorean triple $(b,h,c)$, Plimpton 322 lists 15 of the 16 triples such that $n \leq 60$, $\pi/6 \leq \theta \leq \pi/4$ and $\tan \theta = h^2 / b^2$ has a finite sexagesimal expansion.

The geometric problem given in the Susa tablet is to obtain the radius of the circumscribed circle on an isosceles triangle with sides 50, 50 and 60. A simple algebraic calculation employing Pythagoras' theorem immediately yields that the radius is $\bar{31}.\bar{15} (\mbox{mod } 60)$.

The question on the Tell Dhibayi tablet is to obtain the sides of the rectangle whose area is $0.\bar{45}~ (\mbox{mod } 60)$ and diagonal is $\bar{1}.\bar{15}~ (\mbox{mod } 60)$. Setting up a quadratic equation one immediately obtains that the sides have to be of lengths $1$ and $0.\bar{45}~ (\mbox{mod } 60)$. However, the solution given on the tablet merits a discussion. Using a hybrid of modern notation and sexagesimal arithmetic, let $x$ and $y$ denote the lengths of the two sides. The steps are (i) $2xy = \bar{1}.\bar{30}$, (ii) $x^2 + y^2 - 2xy = (\bar{1}.\bar{15})^2 - \bar{1}.\bar{30} = 0.\bar{3}~\bar{45}$, (iii) $x-y = \sqrt{0.\bar{3}~\bar{45}} = 0.\bar{15}$, (iv) $(x-y)/2 = 0.\bar{7}~\bar{30}$, (v) $((x-y)/2)^2 = 0.\bar{0}~\bar{56}~\bar{15}$, (vi) $((x-y)/2)^2 + (xy) =0.\bar{0}~\bar{56}~\bar{15} + 0.\bar{45}= 0.\bar{45}~\bar{56}~\bar{15}$, (vii) $(x+y)/2 = 0.\bar{52}~\bar{30}$, (viii) $x =((x+y)/2) + ((x-y)/2)=1$, (ix) $y= ((x+y)/2) - ((x-y)/2)= 0.\bar{45}$. Hence the dimensions of the rectangle are $1$ and $0.\bar{45}$.

This clearly demonstrates that the Babylonians were quite conversant with both the geometric and arithmetic properties of the Pythagorean triples. Of course, whether they had a proof of the Pythagras' theorem or, more importantly, whether there was any notion of proof in Babylonian times is a different question and we do not discuss it here.