Model Selection

Deepayan Sarkar

Model selection

  • Regression problems often have many predictors

  • The number of possible models increase rapidly with number of predictors

  • Even if we one of these models is “correct”, how do we find it?

Why does it matter?

  • One solution could be to use all the predictors

  • This is technically a valid model

  • Unfortunately this usually leads to unnecessarily high prediction error

  • Alternative: find “smallest” model for which \(F\)-test comparing to full model is accepted

  • This leads to multiple testing, inflated Type I error probability (and no obvious fix)

  • Model selection is usually based on some alternative criteria developed specifically for that purpose

Underfitting vs overfitting: the bias-variance trade-off

  • The basic problem in model selection is the familiar bias-variance trade-off problem

  • Underfitting leads to biased coefficient estimates

  • Overfitting leads to coefficient estimates with higher variance

Underfitting vs overfitting: the bias-variance trade-off

  • Formally, suppose we fit the two models
\[\begin{eqnarray*} E(\mathbf{y}) &=& \mathbf{X}_1 \beta_1 \\ E(\mathbf{y}) &=& \mathbf{X}_1 \beta_1 + \mathbf{X}_2 \beta_2 = \mathbf{X} \beta \end{eqnarray*}\]

  • If the second model is correct, then \(\hat{\beta}_1^{(1)}\) obtained by fitting the first model will be biased for \(\beta_1\) in general

  • If the first model is correct, then \(\hat{\beta}_1^{(2)}\) obtained by fitting the second model will be unbiased for \(\beta_1\)

  • However, in that case, \(\hat{\beta}_1^{(2)}\) will have higher variance than \(\hat{\beta}_1^{(1)}\) in general; i.e., for any vector \(\mathbf{u}\),

\[ V\left(\mathbf{u}^T \hat{\beta}_1^{(2)} \right) \geq V\left( \mathbf{u}^T \hat{\beta}_1^{(1)} \right) \]

  • Proof: exercise

Model selection criteria

  • Overly simple and overly complex models are both bad

  • Best model usually lies somewhere in the middle

  • How do we find this ideal model?

  • Most common approach: some model-selection criterion measuring overall quality of a model

  • To be useful, such a criterion must punish both overly simple and overly complex models

  • Once criterion is determined, fit a number of different models and choose the best (details later)

  • We will first discuss some possible criteria

Coefficient of determination

  • The simplest model quality measure is \(R^2\)

\[ R^{2}=\frac{T^{2}-S^{2}}{T^{2}} = \frac{\frac{T^{2}}{n}-\frac{S^{2}}{n}}{\frac{T^{2}}{n}} \]

  • Always increases when more predictors are added (does not penalize complexity)

  • Can compare models of same size, but not generally useful for model selection

  • Possible alternative: Adjusted \(R^{2}\) (substitute unbiased estimators of \(\sigma^2\))

\[ R_{adj}^{2}=\frac{\frac{T^{2}}{n-1}-\frac{S^{2}}{n-p}}{\frac{T^{2}}{n-1}}=1-\frac{n-1}{n-p}( 1-R^{2}) \]

Coefficient of determination

  • Maximizing \(R^2\) equivalent to minimizing SSE (or \(\hat{\sigma}^2_{MLE}\))

  • Maximizing \(R_{adj}^2\) equivalent to minimizing unbiased \(\hat{\sigma}^2\)

  • Other than simplicity of interpretation, no particular justification

Cross-validation SSE

  • Use cross-validation to directly assess prediction error

  • Define \[ T_{p}^{2}=\sum_{i=1}^n \left( y_{i} - \bar{y}_{(-i)}\right)^{2} \] and \[ S_{p}^{2} = \sum_{i=1}^n \left( y_{i}-\hat{y}_{i(-i)} \right)^{2} = \sum_{i=1}^n \left( \frac{e_i}{1-h_i} \right)^{2} \]

  • The predictive \(R^{2}\) is defined as \[ R_{p}^{2}=\frac{T_{p}^{2}-S_{p}^{2}}{T_{p}^{2}} \]

  • Equivalently, minimize predictive sum of squares \(S_{p}^{2}\) (often abbreviated as PRESS)

Directly estimating bias and variance

  • More sophisticated approaches attempt to directly estimate bias and variance

  • Suppose true expected value of \(y_i\) is \(\mu_i\)

  • Total mean squared error of a model fit is

\[ MSE = E \sum_i (\hat{y}_i - \mu_i)^2 = \sum_i \left[ (E\hat{y}_i - \mu_i)^2 + V(\hat{y}_i) \right] \]

  • The first term is the “bias sum of squares” \(BSS\) (equals zero if no bias)

  • The second term simplifies to

\[ \sum_i V(\hat{y}_i) = \sigma^2 \sum_i \mathbf{x}_i^T (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{x}_i = \sigma^2 \sum_i h_i = p \sigma^2 \]

Directly estimating bias and variance

  • On the other hand

\[ E(RSS) = E \sum_i ( y_i - \hat{y}_i)^2 = E (\mathbf{y}^T (\mathbf{I} - \mathbf{H}) \mathbf{y} ) \]

  • This equals \((n-p) \sigma^2\) when \(\hat{y}_i\)-s are unbiased

  • If \(\hat{y}_i\)-s are biased, it can be shown that this term equals \(BSS + (n-p) \sigma^2\)

  • This gives the following estimator of \(MSE\) (up to unknown \(\sigma^2\))

\[ RSS - (n-p) \sigma^2 + p \sigma^2 = RSS + (2p-n) \sigma^2 \]

Mallow’s \(C_p\)

  • Dividing by \(\sigma^2\) on both sides, this gives Mallow’s \(C_p\) criterion

\[ C_p = \frac{RSS}{\sigma^2} + 2p - n \]

  • This requires an estimate of \(\sigma^2\)

  • It is customary to use \(\hat{\sigma}^2\) from the largest model

  • If model has no bias, then \(C_p \approx p\) (exact for largest model by definition)

  • An alternative expression for \(C_p\) is (exercise)

\[ C_p = (p_f - p) (F - 1) + p \]

  • where
    • \(p_f\) is the number of coefficients in the largest model (used to estimate \(\sigma^2\))
    • \(F\) is the \(F\)-statistic comparing the model being evaluated with the largest model
  • Again, if the model is “correct”, then \(F \approx 1\), so \(C_p \approx p\)

Likelihood based criterion

  • A more general approach is to prefer models that improve the expected log-likelihood

\[ E \sum_i \log P_{\hat{\theta}}(y_i) \]

  • Here the expectation is over two independent sets of the true distribution of \(\mathbf{y}\)

  • One set of \(\mathbf{y}\) is used to estimate \(\hat\theta\)

  • Akaike showed that

\[ - 2E \sum_i \log P_{\hat{\theta}}(y_i) \approx -2 E (\text{loglik}) + 2p \]

  • Here \(\text{loglik}\) is the maximized log-likelihood for the fitted model

Akaike Information Criterion

  • This suggests the Akaike Information Criterion (AIC)

\[ \text{AIC} = -2 \text{loglik} + 2p \]

  • For linear models, this is equivalent to (up to a constant)

\[ \text{AIC} = n \log RSS + 2p \]

  • An advantage of AIC over \(C_p\) is that it does not require an estimate of \(\sigma^2\)

  • It is also applicable more generally (e.g., for GLMs)

Bayesian Information Criterion

  • A similar criterion is the Bayesian Information Criterion (BIC)

\[ \text{BIC} = -2 \text{loglik} + p \log n \]

  • As suggested by its name, this is derived using a Bayesian approach

  • The complexity penalty for BIC is higher (except for small \(n\)), so favours simpler models

Example: SLID data — comparing pre-determined set of models

'data.frame':   3987 obs. of  5 variables:
 $ log.wages: num  2.36 2.4 2.88 2.64 2.1 ...
 $ sex      : Factor w/ 2 levels "Female","Male": 2 2 2 1 2 1 1 1 2 2 ...
 $ edu.sq   : num  225 174 196 256 225 ...
 $ age      : int  40 19 46 50 31 30 61 46 43 17 ...
 $ language : Factor w/ 3 levels "English","French",..: 1 1 3 1 1 1 1 3 1 1 ...

Example: SLID data — \(R^2\) and adjusted \(R^2\)

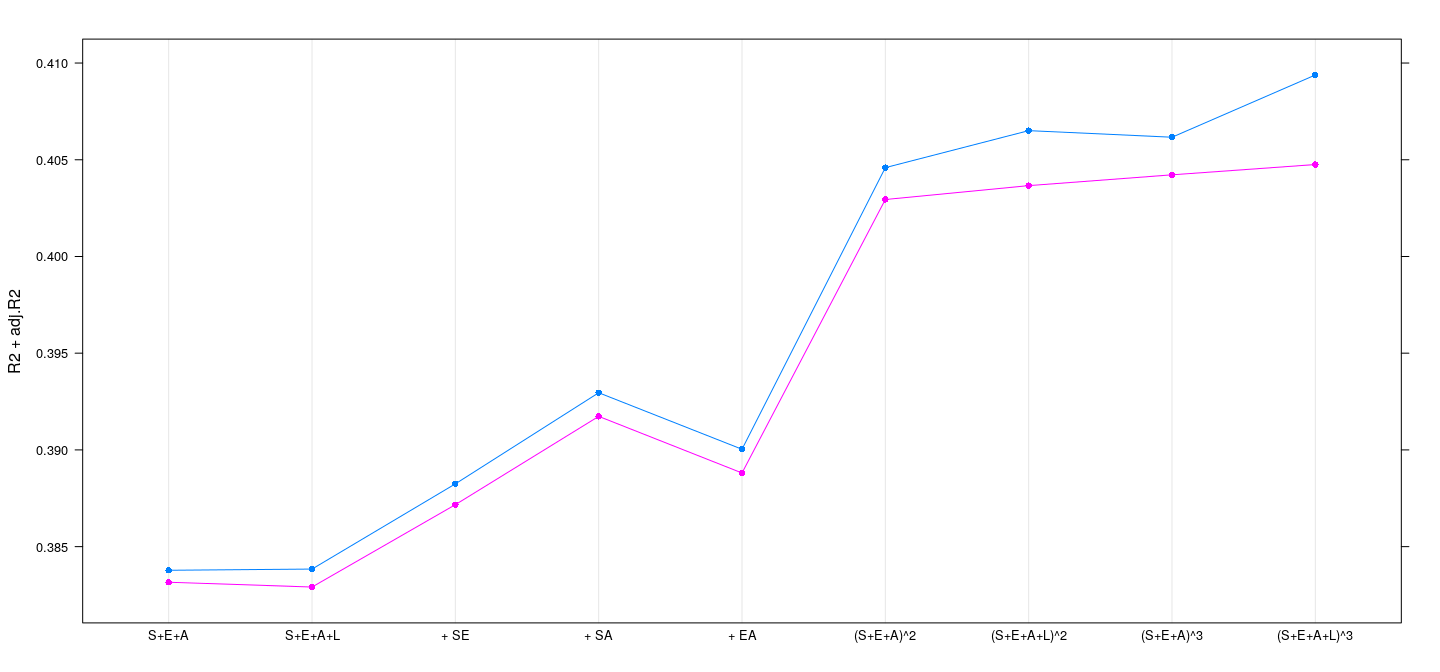
plot of chunk unnamed-chunk-2

Example: SLID data — prediction SS

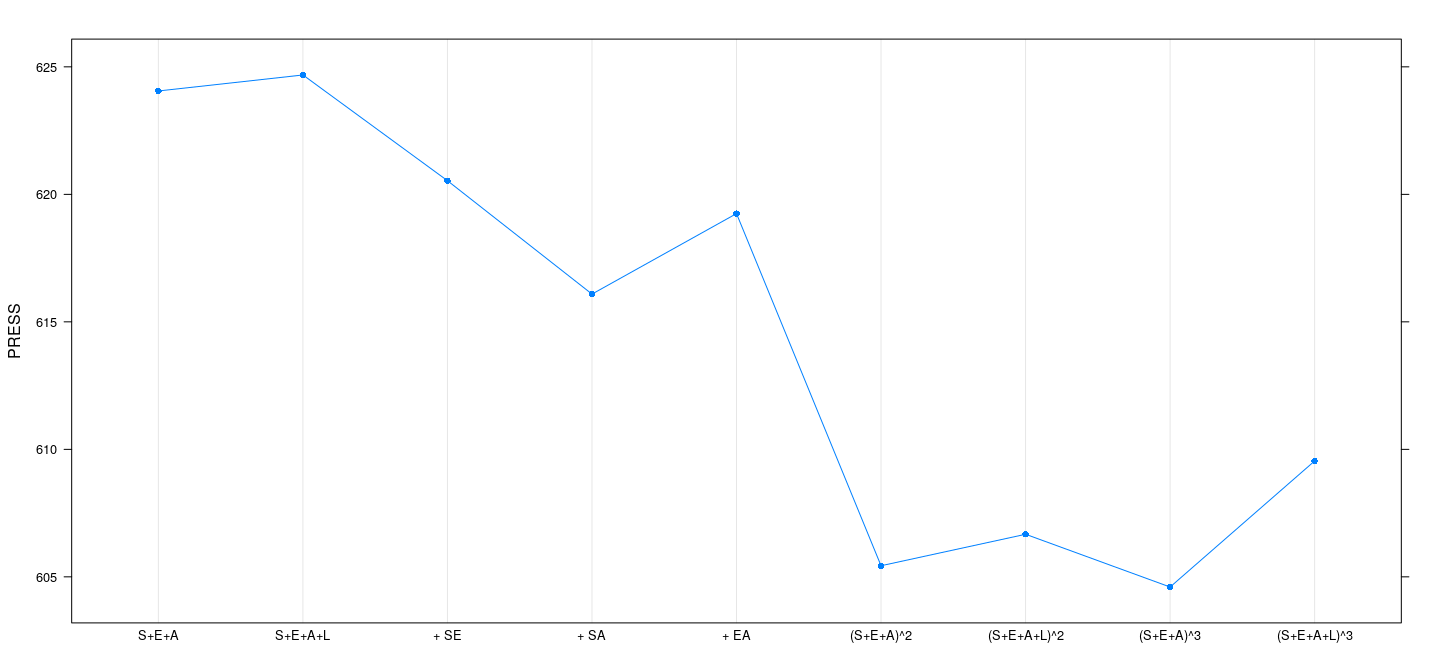
plot of chunk unnamed-chunk-3

Example: SLID data — Mallow’s \(C_p\)

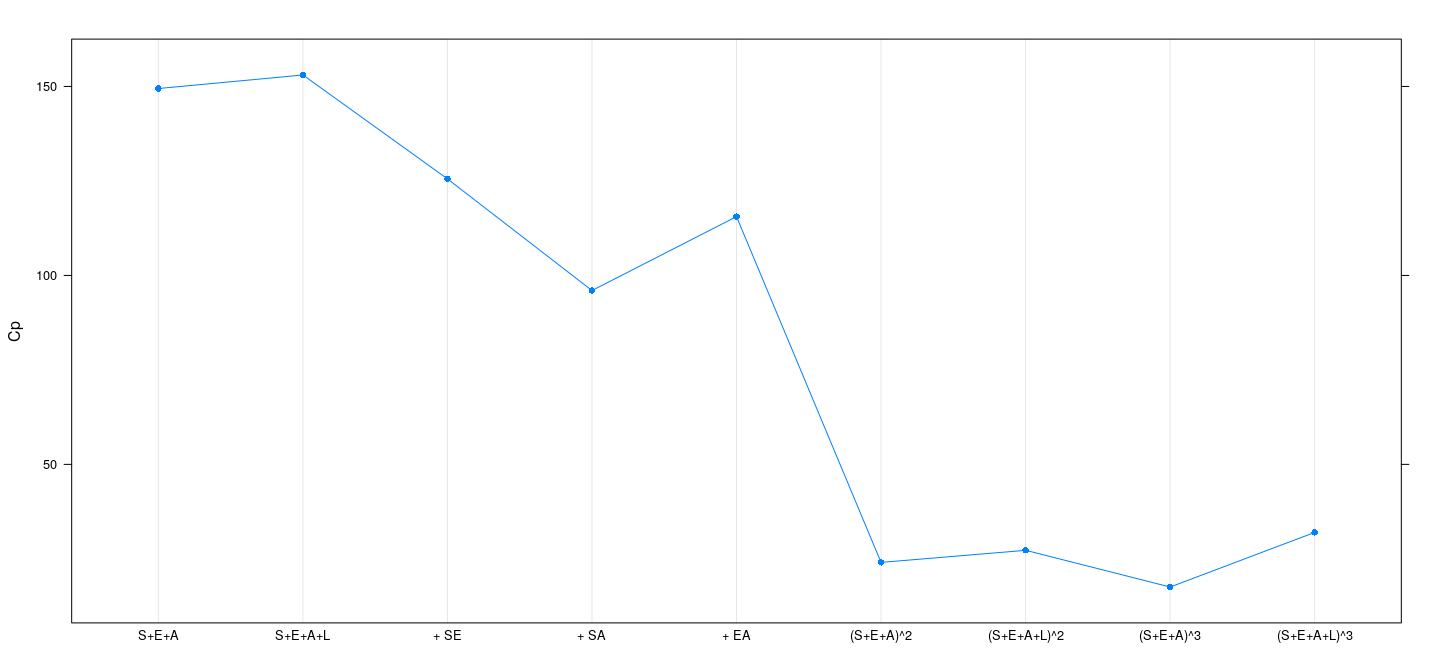
plot of chunk unnamed-chunk-4

Example: SLID data — AIC

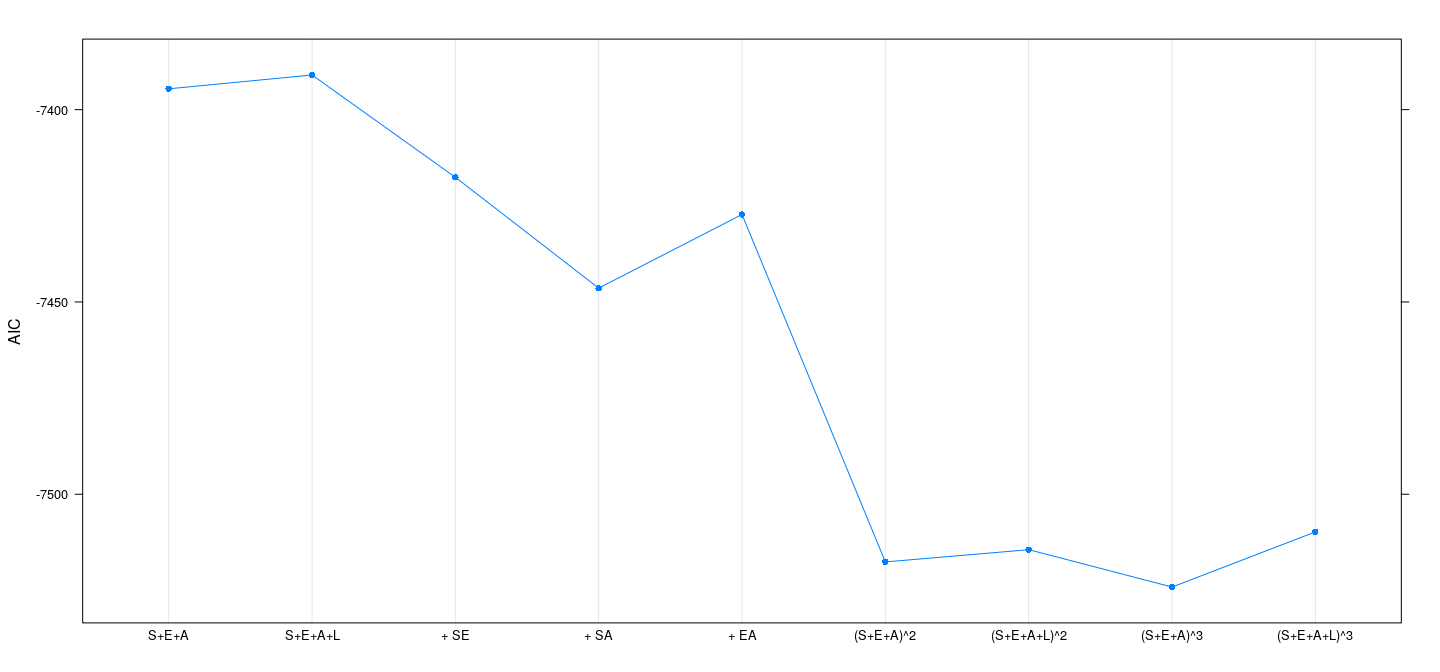
plot of chunk unnamed-chunk-5

Example: SLID data — BIC

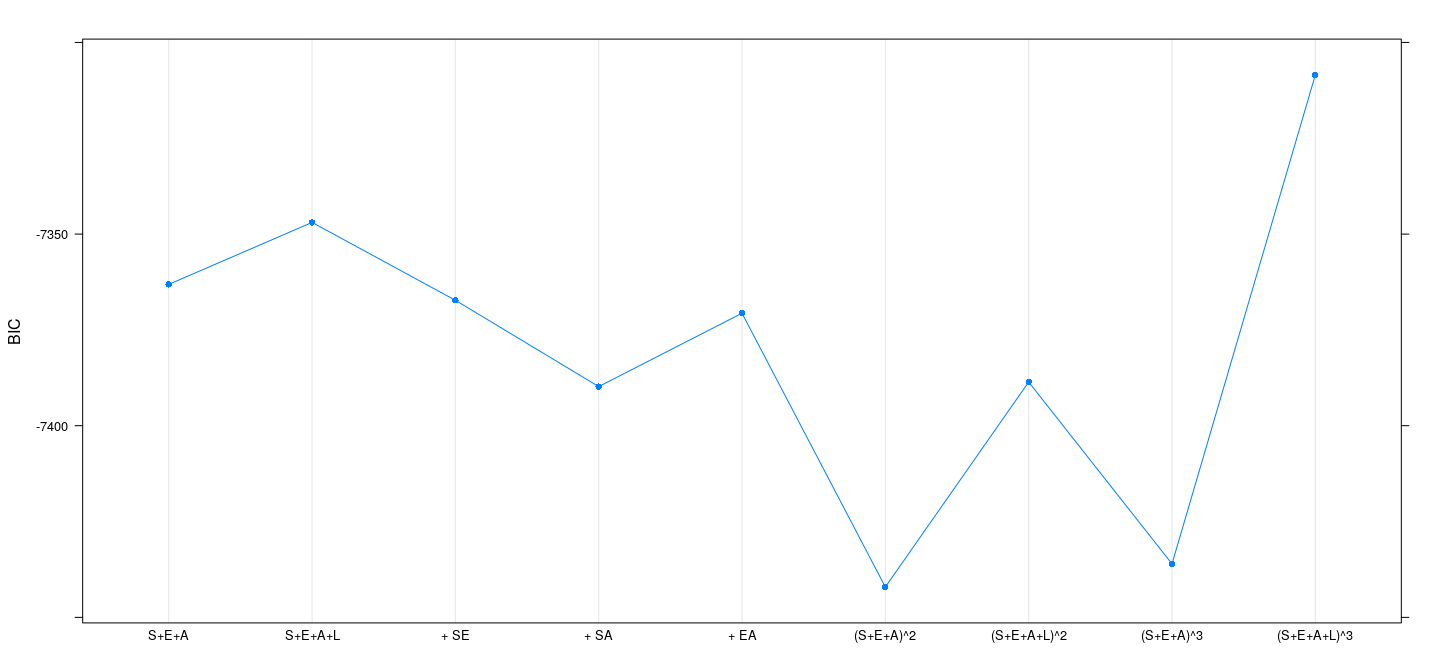
plot of chunk unnamed-chunk-6

Automatic model selection

  • This process still requires us to construct a list of models to consider

  • In general, the number of possible models can be large

  • With \(k\) predictors, there are \(2^k\) additive models, many more with interactions

  • How do we select the “best” out of all possible models?

  • Two common strategies

    • Best subset selection: exhaustive search of all possible models
    • Stepwise selection: add or drop one term at a time (only benefit: needs less time)

Best subset selection: exhaustive search

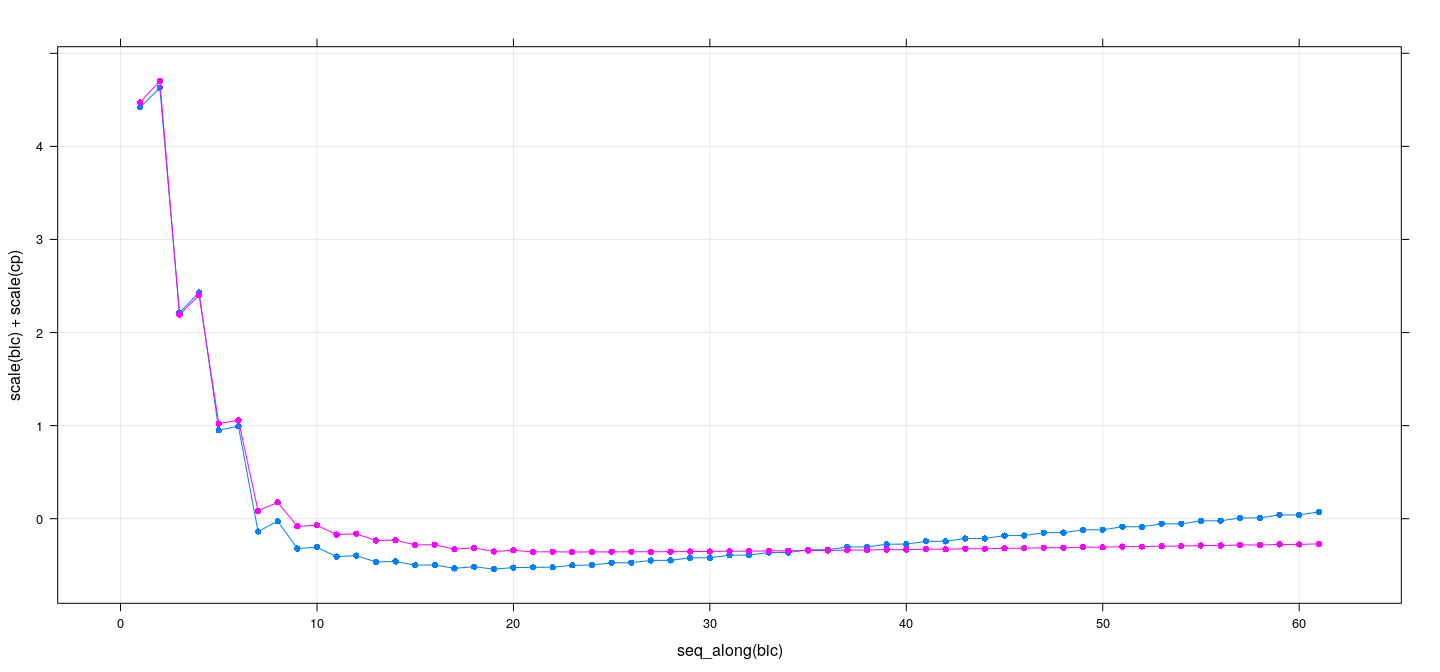
plot of chunk unnamed-chunk-8

Best subset selection: exhaustive search

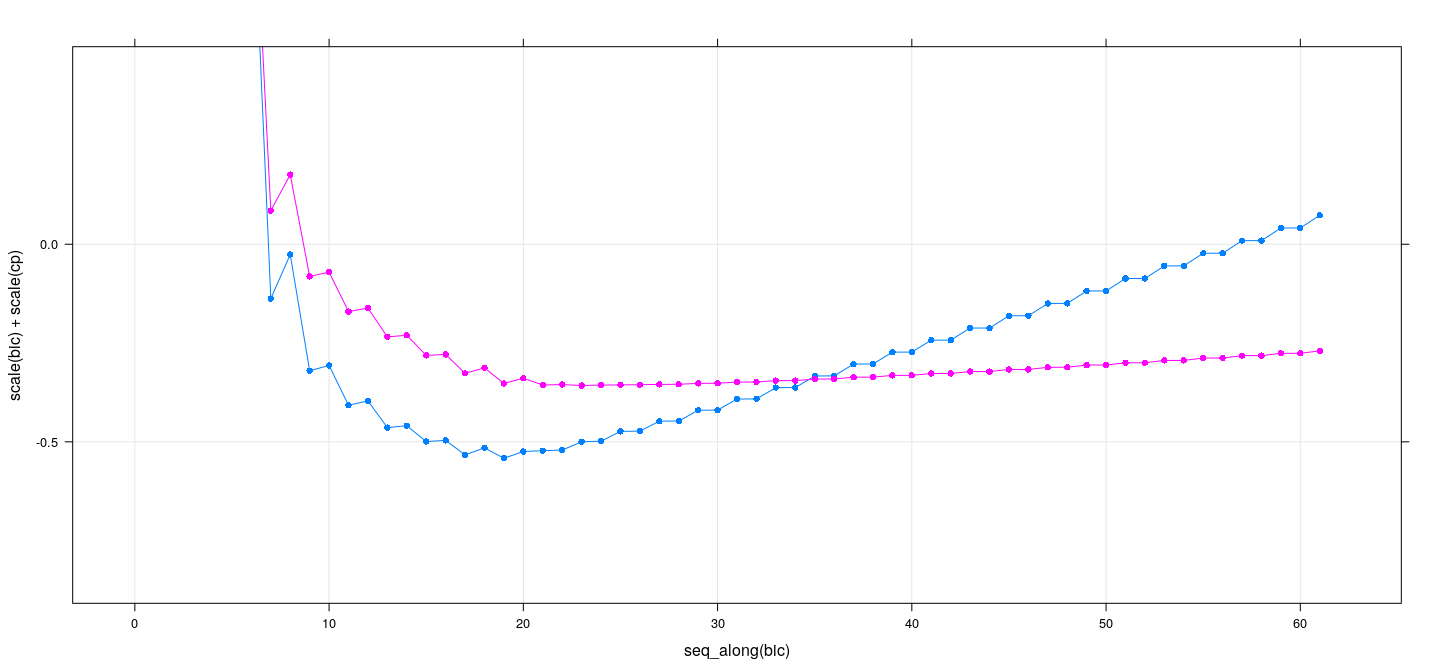
plot of chunk unnamed-chunk-9

Best subset selection: exhaustive search

plot of chunk unnamed-chunk-10

Best subset selection: exhaustive search

plot of chunk unnamed-chunk-11

Handling dummy variables, interactions, etc.

  • One problem with this approach: considers each column of \(\mathbf{X}\) separately

  • Usually we would keep or drop all columns for a term (factor, polynomial) together

  • Similarly, an interaction term usually not meaningful without main effects and lower order interactions

  • Such considerations are not automated by regsubsets() and have to be handled manually

Best subset selection: stepwise search

  • Forward selection
    • Find best one-variable model
    • Find best two-variable model by adding another variable
    • and so on

  • That is, do not look at all two-variable models; only ones that contain the best one-variable model

  • Backward selection: start with full model and eliminate variables successively

  • Sequential replacement: consider both adding and dropping in each step

  • Stepwise selection is supported by regsubsets()

  • Also implemented in MASS::stepAIC() and stats::step()

Best subset selection: forward selection

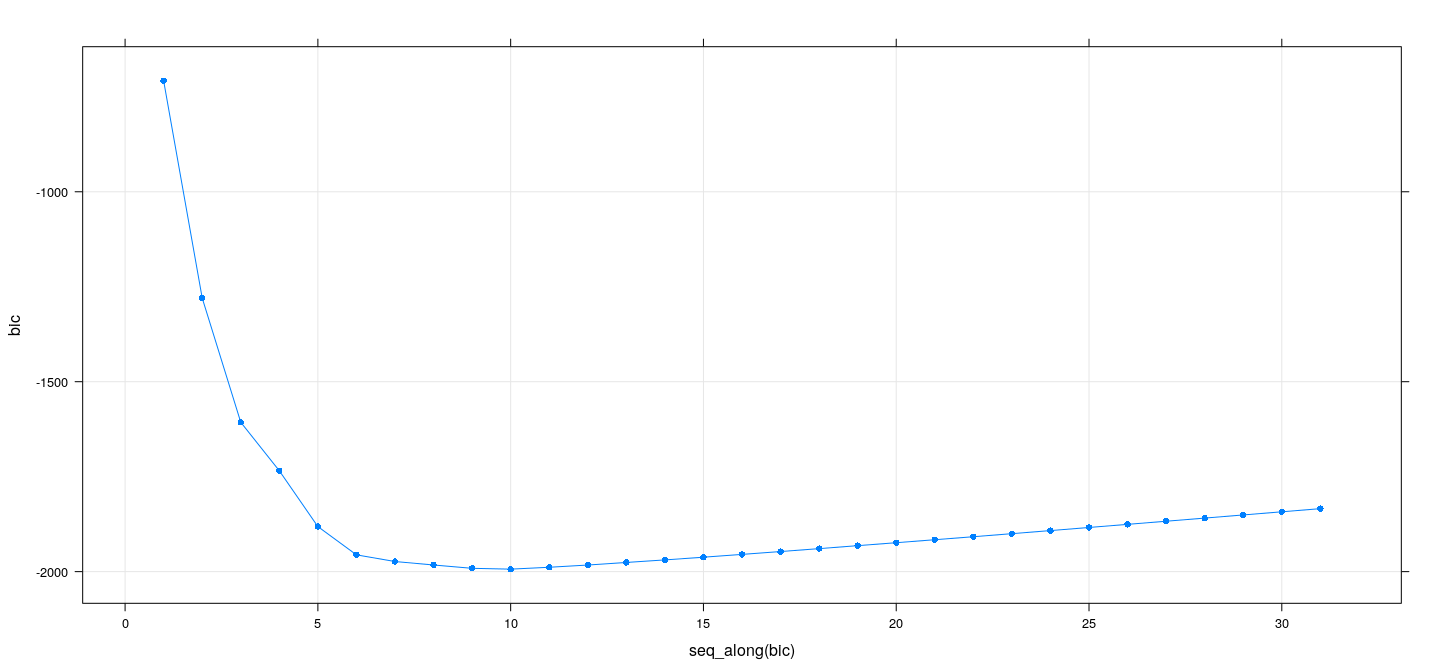
plot of chunk unnamed-chunk-12

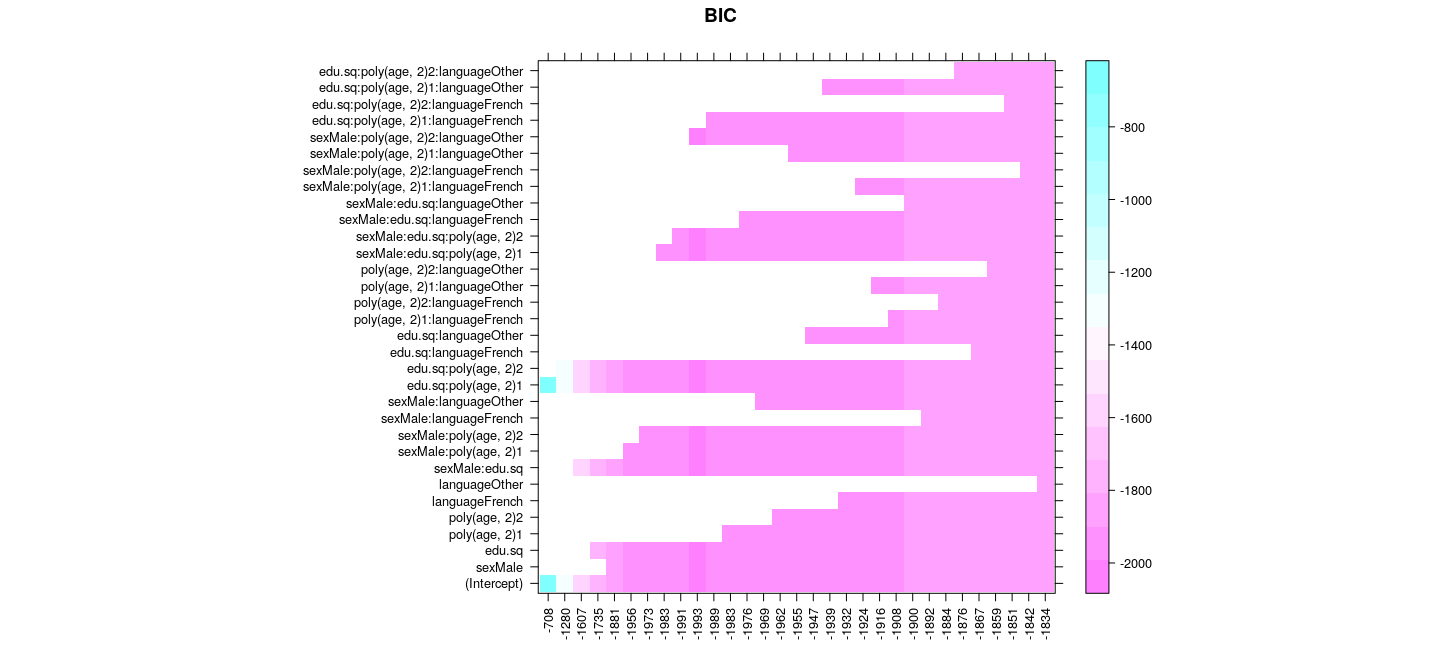
Best subset selection: forward selection

plot of chunk unnamed-chunk-13

Best subset selection: sequential replacement

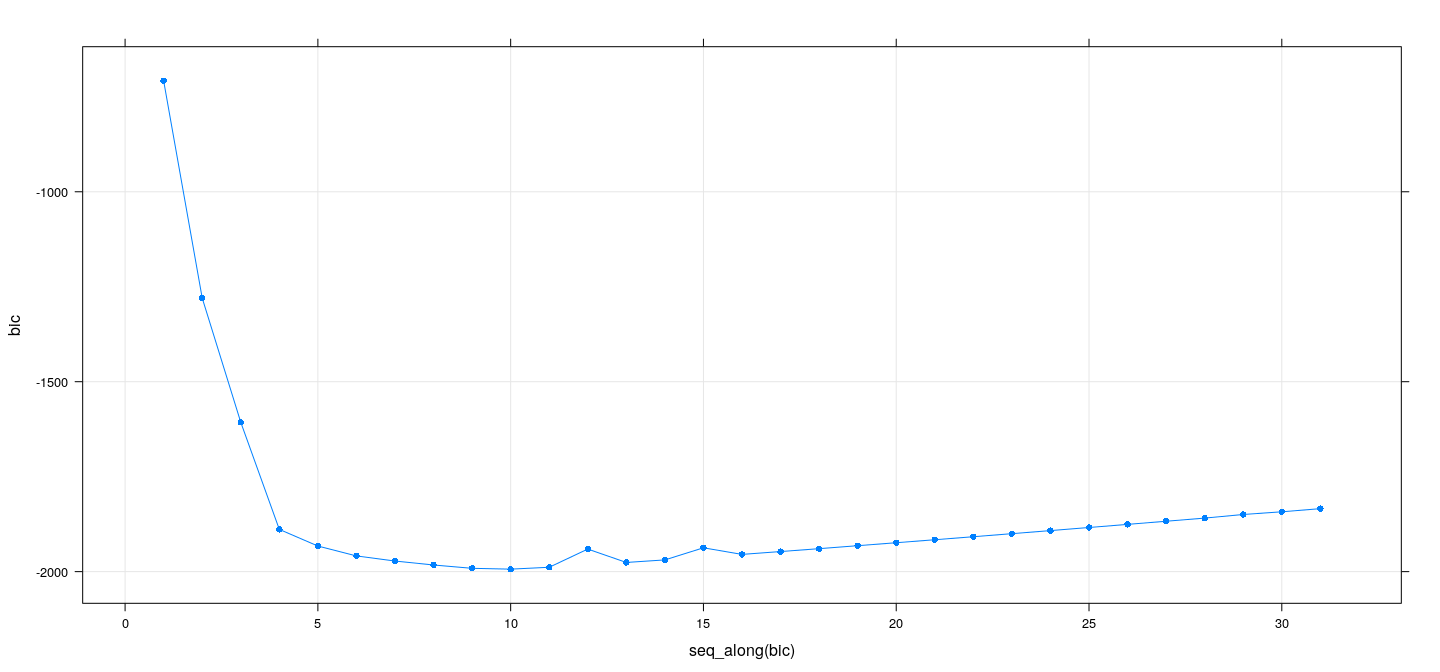
plot of chunk unnamed-chunk-14

Best subset selection: sequential replacement

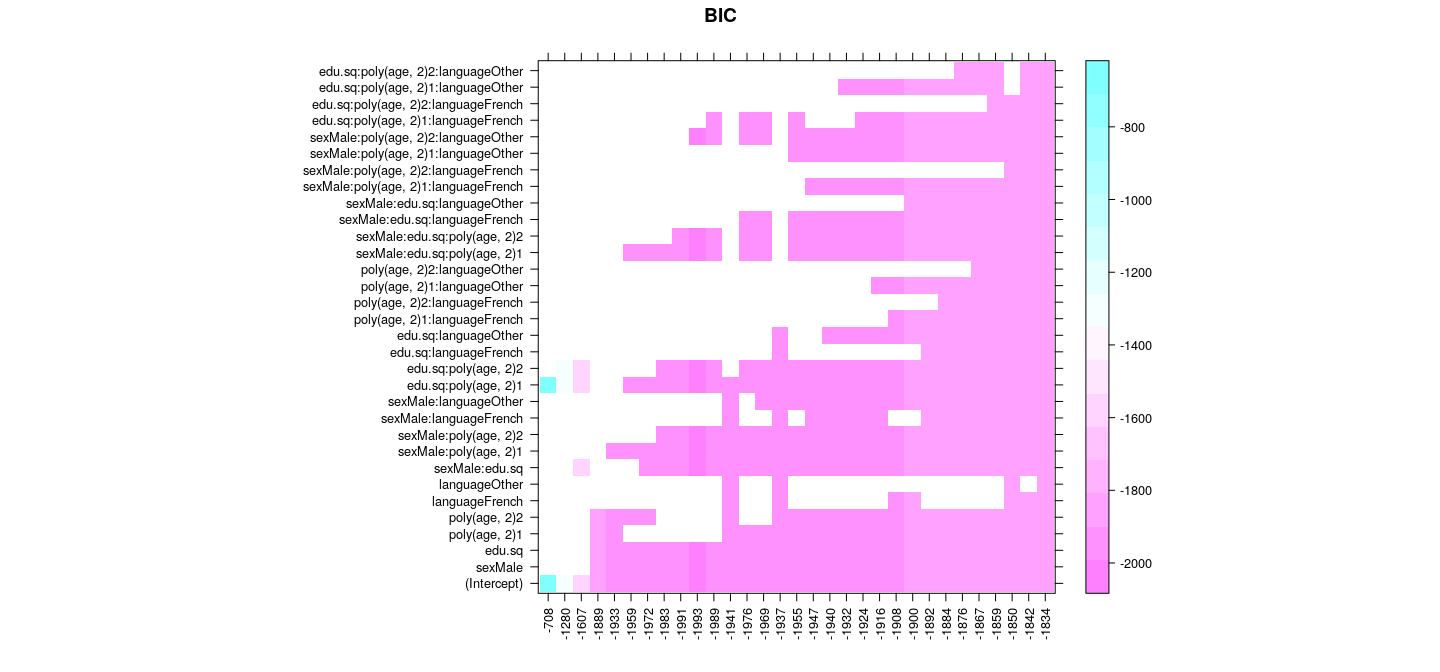
plot of chunk unnamed-chunk-15

Benefits and drawbacks of automated model selection

  • Can quickly survey a large number of potential models

  • However, there are many drawbacks to this approach

  • In fact, automated model selection basically invalidates inference

  • This is because all derivations assume that model and hypotheses are prespecified

  • As a result, for the model chosen by automated selection

    • Test statistics no longer follow \(t\) / \(F\) distributions

    • Standard errors have negative bias, and confidence intervals are falsely narrow

    • \(p\)-values are falsely small

    • Regression coefficients are biased away from 0

Simulation example: no predictive relationship

  • Simulate \(V_2, \dots, V_{21} \sim \text{ i.i.d. } N(0, 1)\)

  • Simulate independent \(V_1 \sim N(0, 1)\)

  • Regress \(V_1\) on \(V_2, \dots, V_{21}\)

  • Select model using stepAIC()

Simulation example: no predictive relationship


Call:
lm(formula = V1 ~ V2 + V3 + V6 + V9 + V13, data = d)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.20598 -0.59320 -0.05848  0.56056  2.34801 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) -0.03006    0.08906  -0.338  0.73645   
V2           0.13104    0.09139   1.434  0.15493   
V3          -0.16376    0.08943  -1.831  0.07026 . 
V6          -0.29802    0.10074  -2.958  0.00391 **
V9           0.15936    0.08864   1.798  0.07542 . 
V13          0.17006    0.08214   2.070  0.04116 * 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.8665 on 94 degrees of freedom
Multiple R-squared:  0.1932,    Adjusted R-squared:  0.1503 
F-statistic: 4.501 on 5 and 94 DF,  p-value: 0.001011
     value 
0.00101054

Simulation example: no predictive relationship

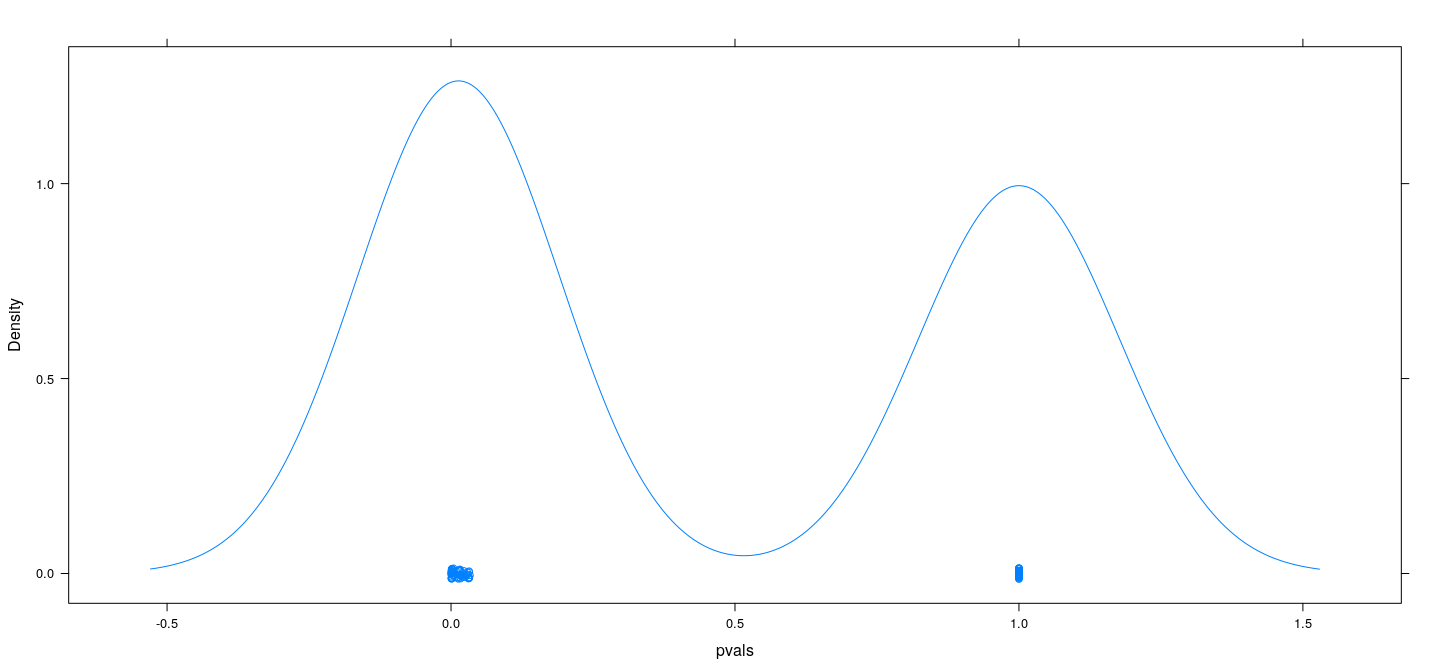
[1] 84

Simulation example: no predictive relationship

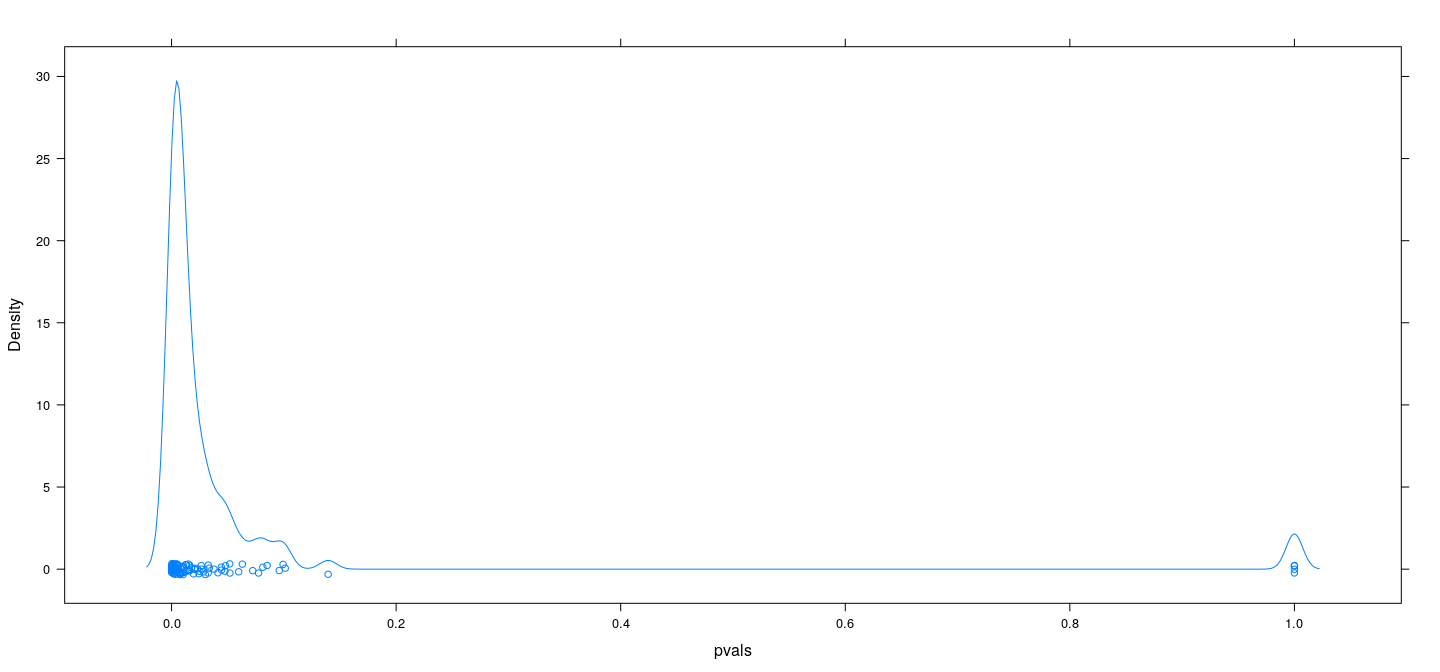
plot of chunk unnamed-chunk-19

Simulation example: no predictive relationship

  • Results are slightly better when using BIC rather than AIC, but still bad

  • Select model using stepAIC(..., k = log(n))

[1] 56

Simulation example: no predictive relationship

plot of chunk unnamed-chunk-21

Summary

  • Automated model selection has its uses

  • However, blindly applying it without thinking about the problem is dangerous

  • Many applied studies have no prespecified hypothesis

  • Especially in observational studies (e.g., public health and social sciences)

  • Model is often chosen by automated selection, but interpreted as if prespecified

  • Result: much more than 5% of “significant” results are probably false