Introduction to Nonparametric Regression
Deepayan Sarkar
Visualizing distributions
Recall that the goal of regression is to predict distribution of \(\mathbf{Y} | \mathbf{X=x}\)
How can we assess distribution visually? (e.g., to check normality)
Usual tools
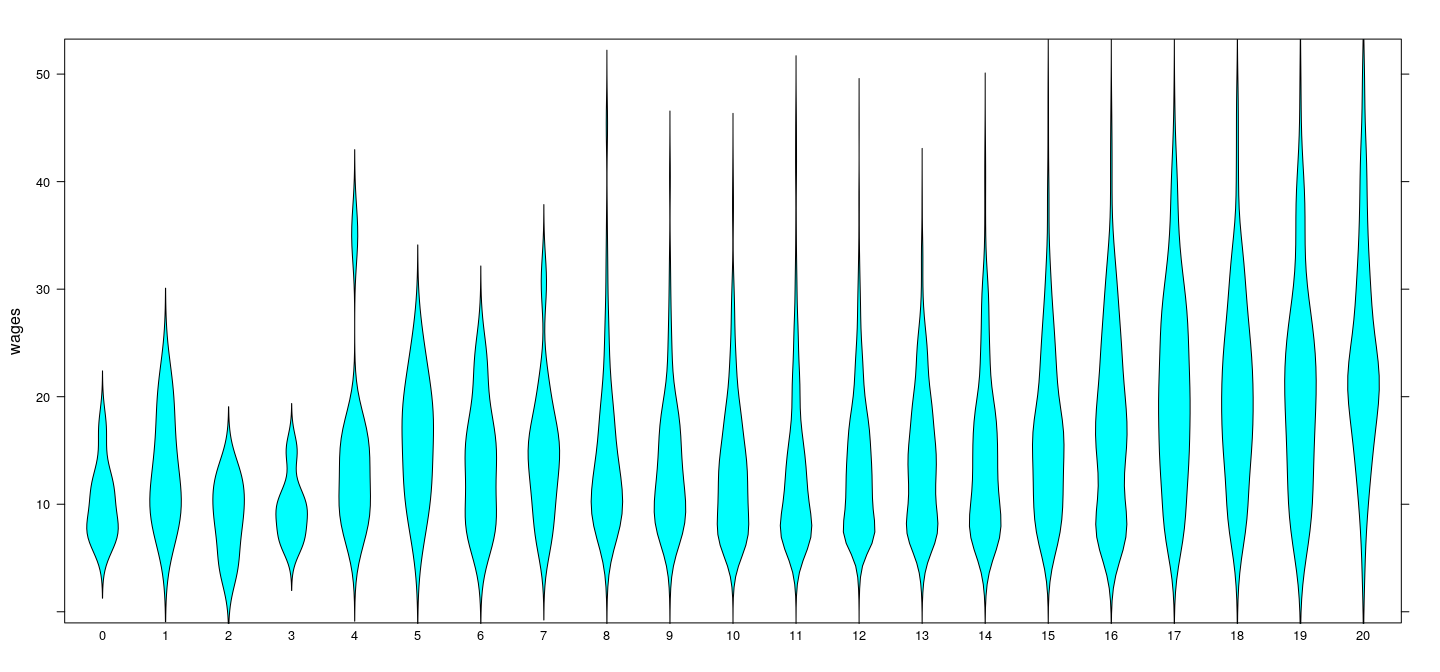
- Histograms / density plots
- Box-and-whisker plots
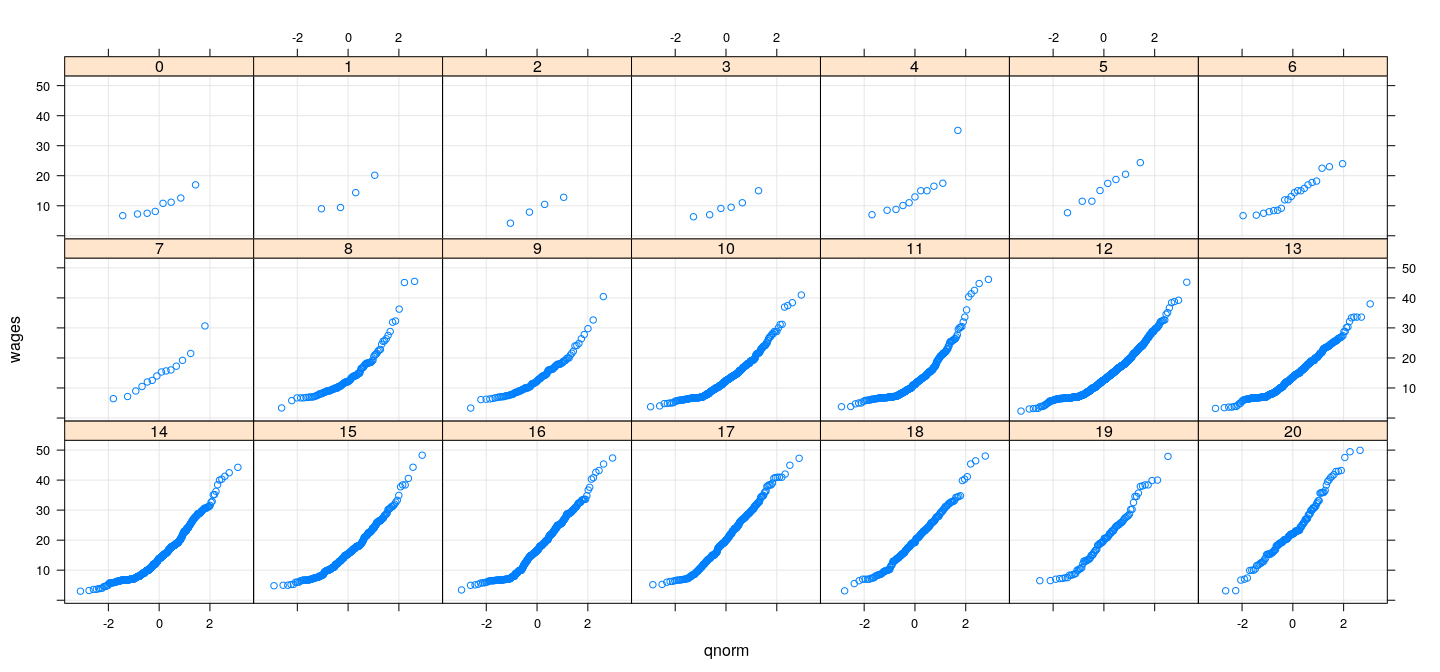
- Quantile-quantile plots
Example: SLID data

Example: SLID data (rounding education)
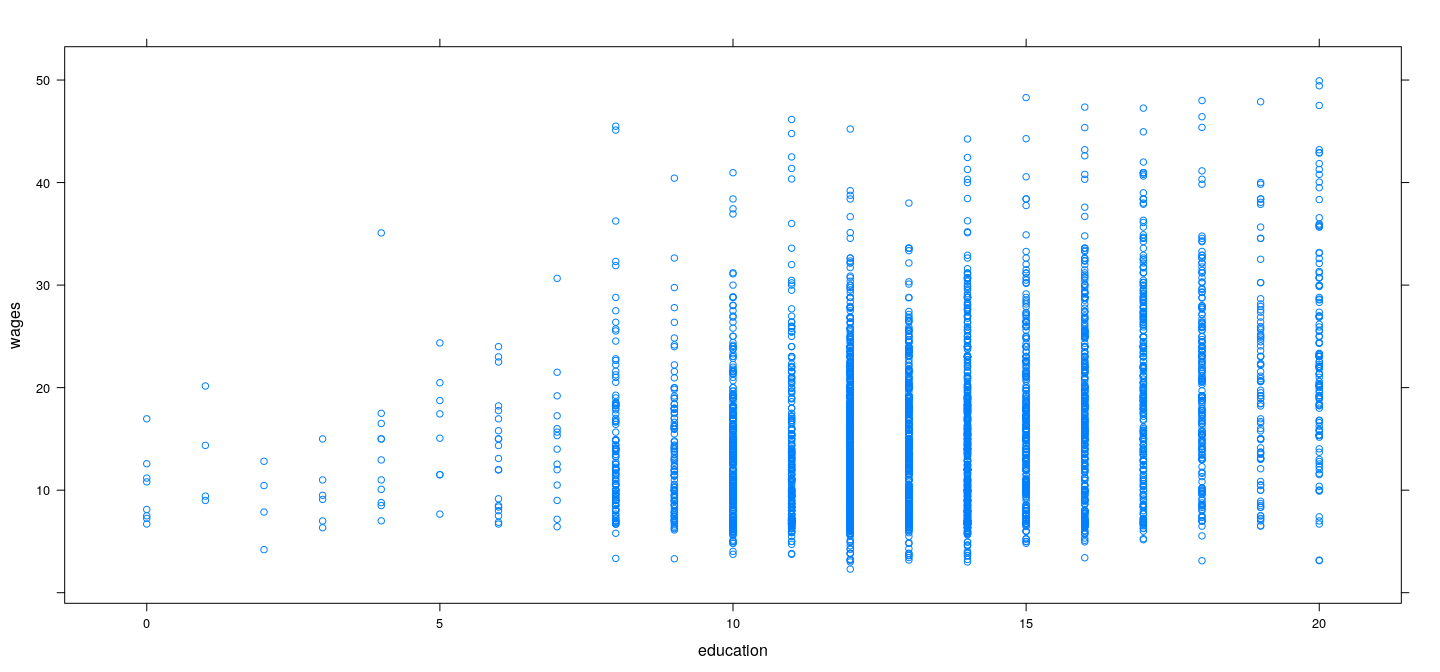
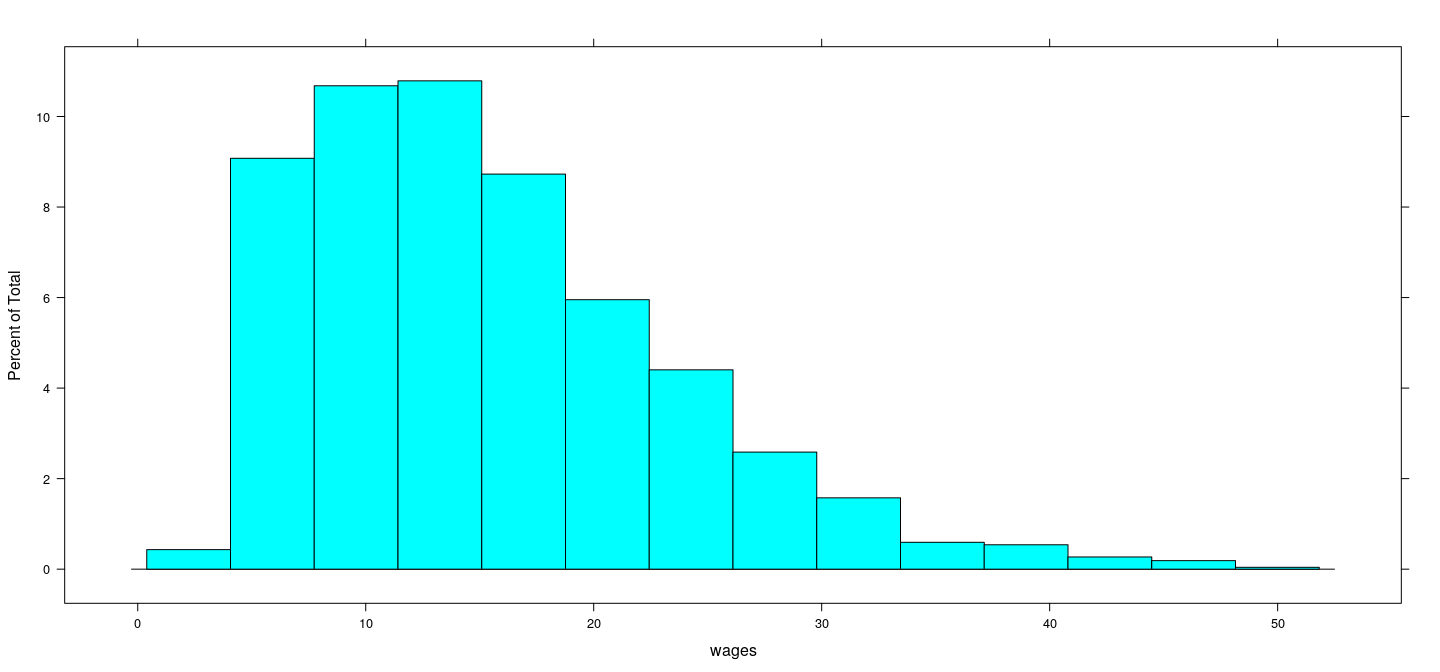
Distribution of wages (overall)
Distribution of wages (conditional on education)
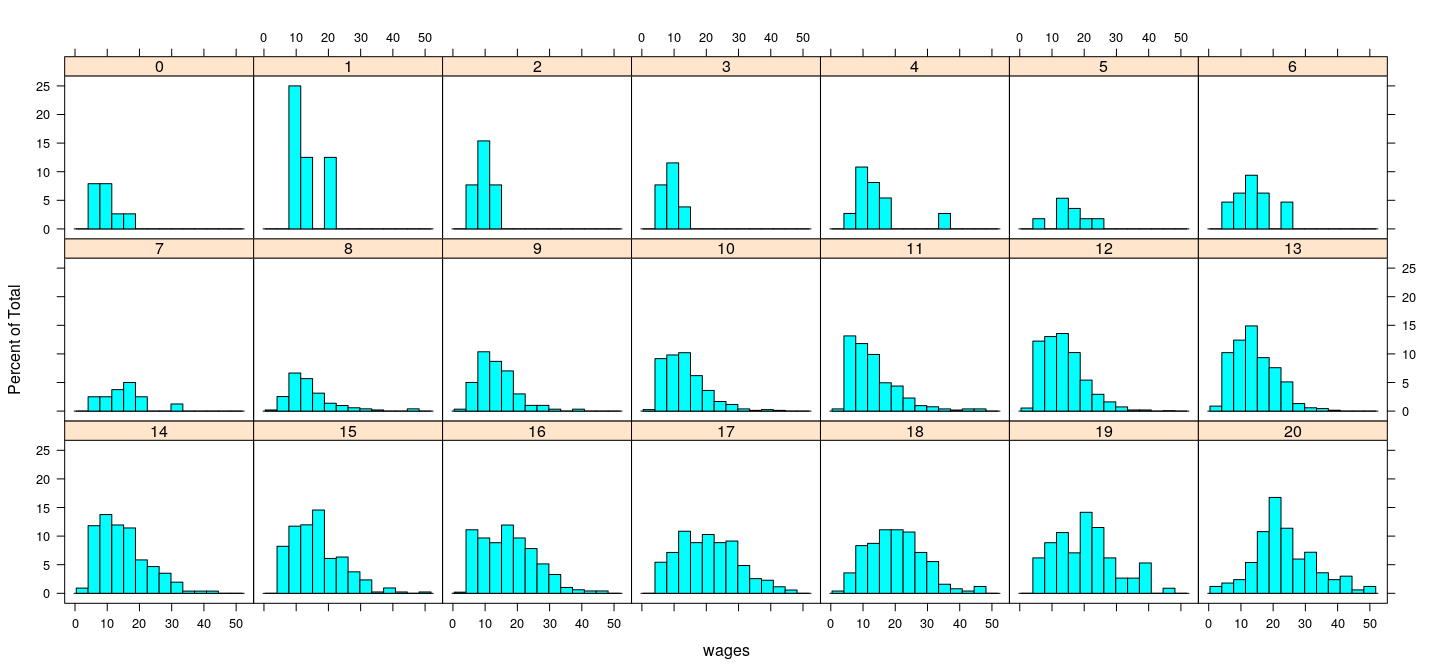
Distribution of wages (conditional on education)
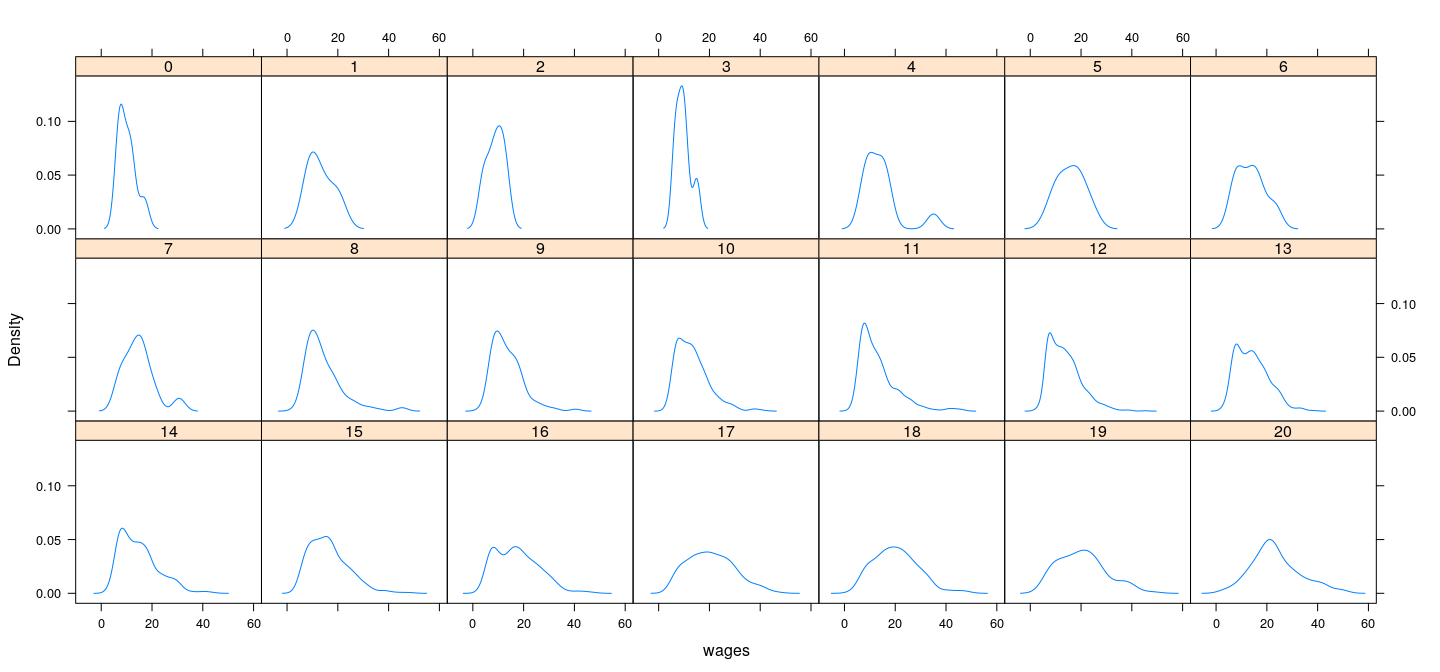
Distribution of wages (conditional on education)
More direct comparison
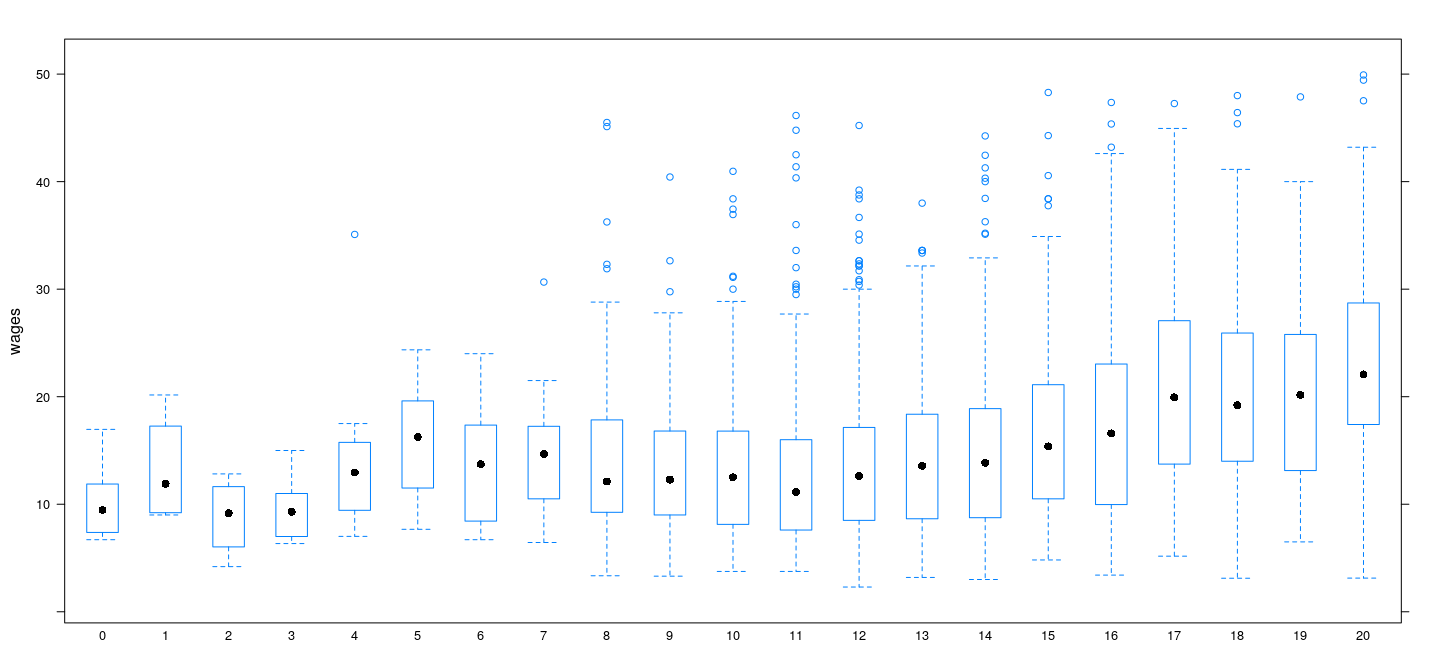
More direct comparison
Pure error model
- Corresponding linear model is called the pure error model (assuming equal variance)
fm.linear <- lm(wages ~ education, data = SLID) # for comparison
fm.pe <- lm(wages ~ factor(education), data = SLID)
summary(fm.linear)
Call:
lm(formula = wages ~ education, data = SLID)
Residuals:
Min 1Q Median 3Q Max
-17.649 -5.796 -1.005 4.133 34.139
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.0829 0.5304 9.584 <2e-16 ***
education 0.7848 0.0388 20.226 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.5 on 4012 degrees of freedom
(3411 observations deleted due to missingness)
Multiple R-squared: 0.09253, Adjusted R-squared: 0.09231
F-statistic: 409.1 on 1 and 4012 DF, p-value: < 2.2e-16Pure error model
Call:
lm(formula = wages ~ factor(education), data = SLID)
Residuals:
Min 1Q Median 3Q Max
-20.393 -5.670 -1.067 4.060 32.834
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.1375 2.6133 3.879 0.000107 ***
factor(education)1 3.1000 4.5264 0.685 0.493470
factor(education)2 -1.3025 4.5264 -0.288 0.773551
factor(education)3 -0.4808 3.9920 -0.120 0.904132
factor(education)4 4.1743 3.4346 1.215 0.224297
factor(education)5 5.7100 3.6958 1.545 0.122429
factor(education)6 3.5995 3.0922 1.164 0.244463
factor(education)7 4.6654 3.2760 1.424 0.154496
factor(education)8 4.2245 2.7043 1.562 0.118327
factor(education)9 3.4266 2.7059 1.266 0.205455
factor(education)10 3.2118 2.6446 1.214 0.224633
factor(education)11 3.1782 2.6529 1.198 0.230994
factor(education)12 3.5089 2.6248 1.337 0.181355
factor(education)13 4.0991 2.6375 1.554 0.120223
factor(education)14 4.7441 2.6335 1.801 0.071714 .
factor(education)15 6.3196 2.6499 2.385 0.017133 *
factor(education)16 7.3000 2.6438 2.761 0.005786 **
factor(education)17 10.5326 2.6545 3.968 7.38e-05 ***
factor(education)18 10.1605 2.6714 3.803 0.000145 ***
factor(education)19 10.3711 2.7322 3.796 0.000149 ***
factor(education)20 13.3853 2.6970 4.963 7.23e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.392 on 3993 degrees of freedom
(3411 observations deleted due to missingness)
Multiple R-squared: 0.1227, Adjusted R-squared: 0.1183
F-statistic: 27.93 on 20 and 3993 DF, p-value: < 2.2e-16Pure error model
Analysis of Variance Table
Response: wages
Df Sum Sq Mean Sq F value Pr(>F)
factor(education) 20 30522 1526.08 27.931 < 2.2e-16 ***
Residuals 3993 218164 54.64
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Analysis of Variance Table
Model 1: wages ~ education
Model 2: wages ~ factor(education)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 4012 225674
2 3993 218164 19 7510.3 7.2347 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Pure error model
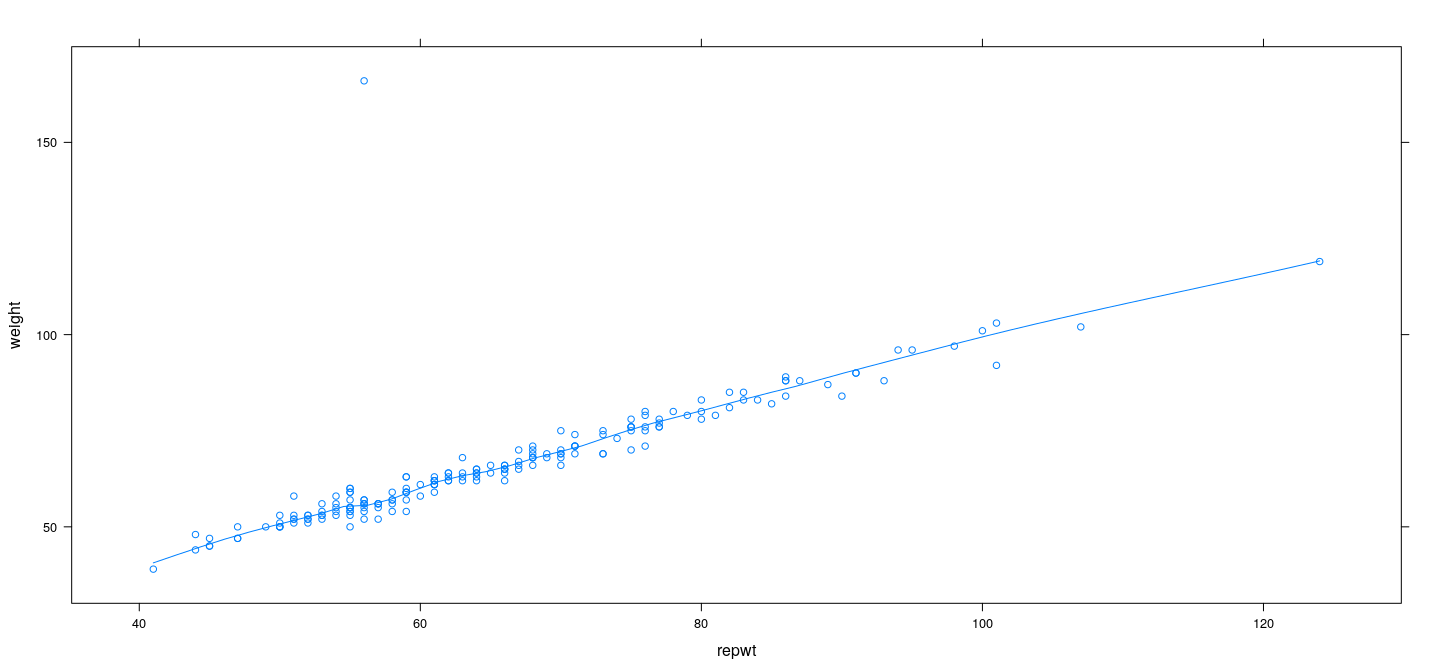
plot(wages ~ jitter(education), data = SLID)
lines(0:20, predict(fm.pe, newdata = data.frame(education = 0:20)))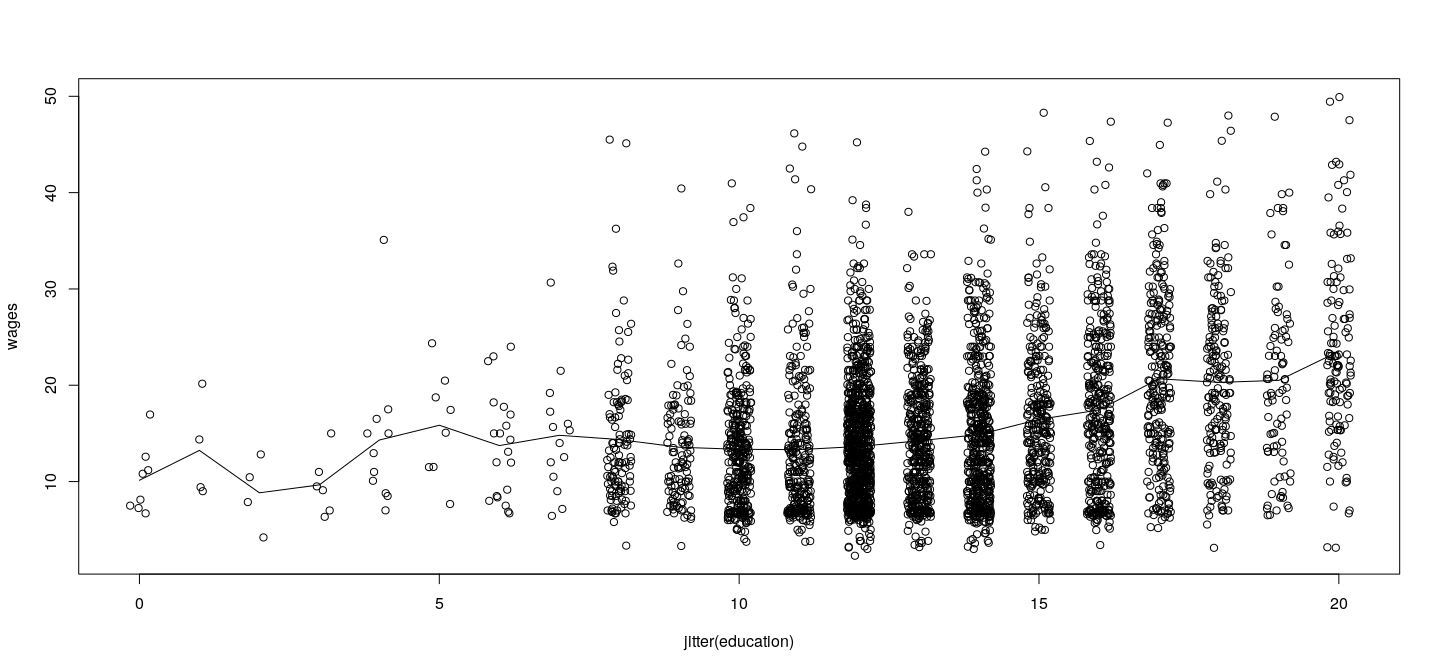
Pure error model
Such comparison possible when lots of data, few unique covariate values
Can be used to assess “non-linearity”
But need graphical tools to assess
- Skewness
- Multiple modes
- “Heavy” tails
- Unequal variance / spread
But what can we do when covariate \(x\) is continuous?
weight ~ heightprestige ~ income
Continuous predictor
Even with large datasets, replicated \(x\) will be rare
We can still divide range of \(x\) into several bins
- Width of bin represents trade-off (for non-linear relationship)
- How “locally” we can estimate (bias of estimator)
- Number of data points (variance of estimator)
Example: Prestige data
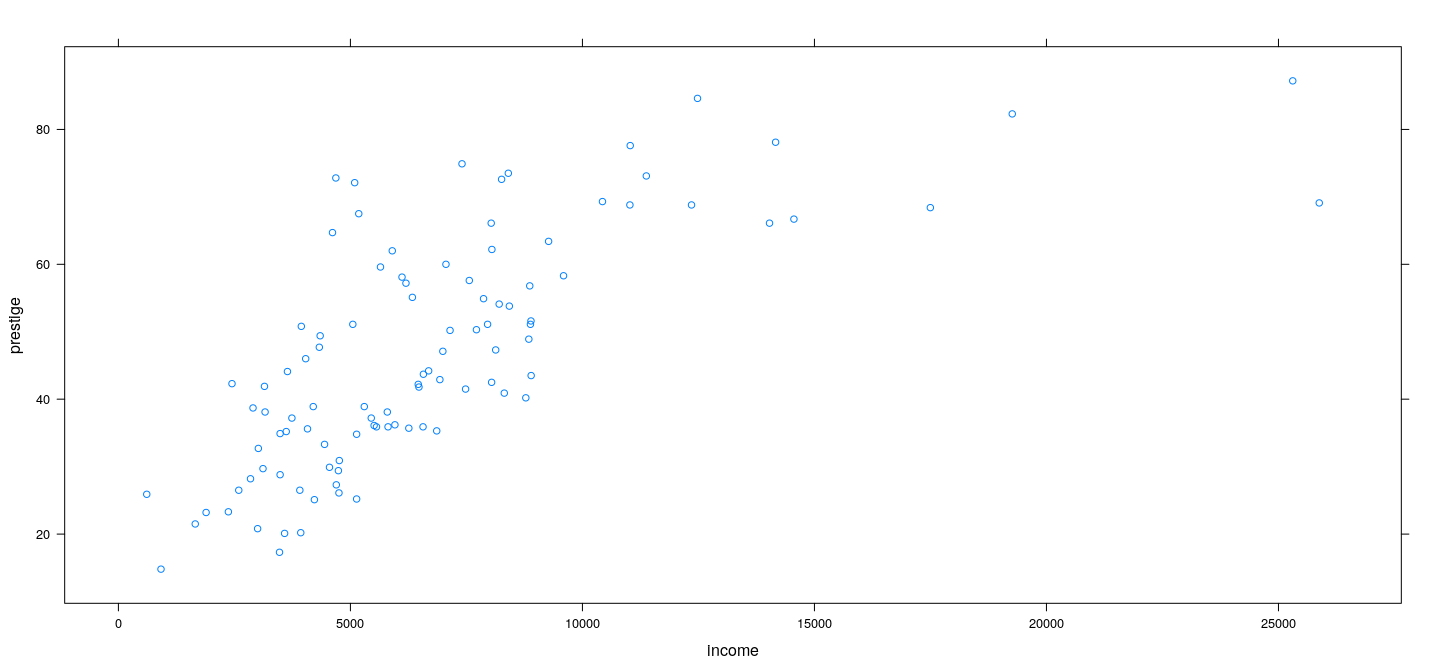
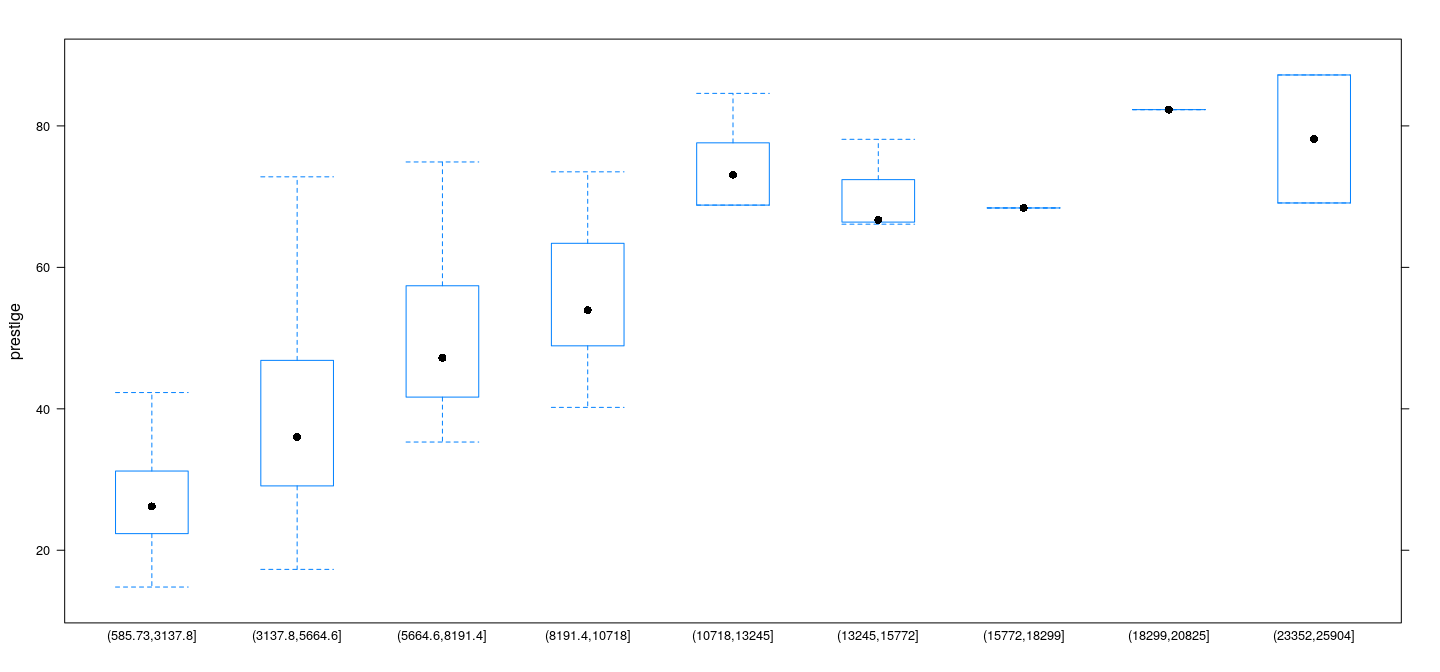
Example: Prestige data
Example: Davis data
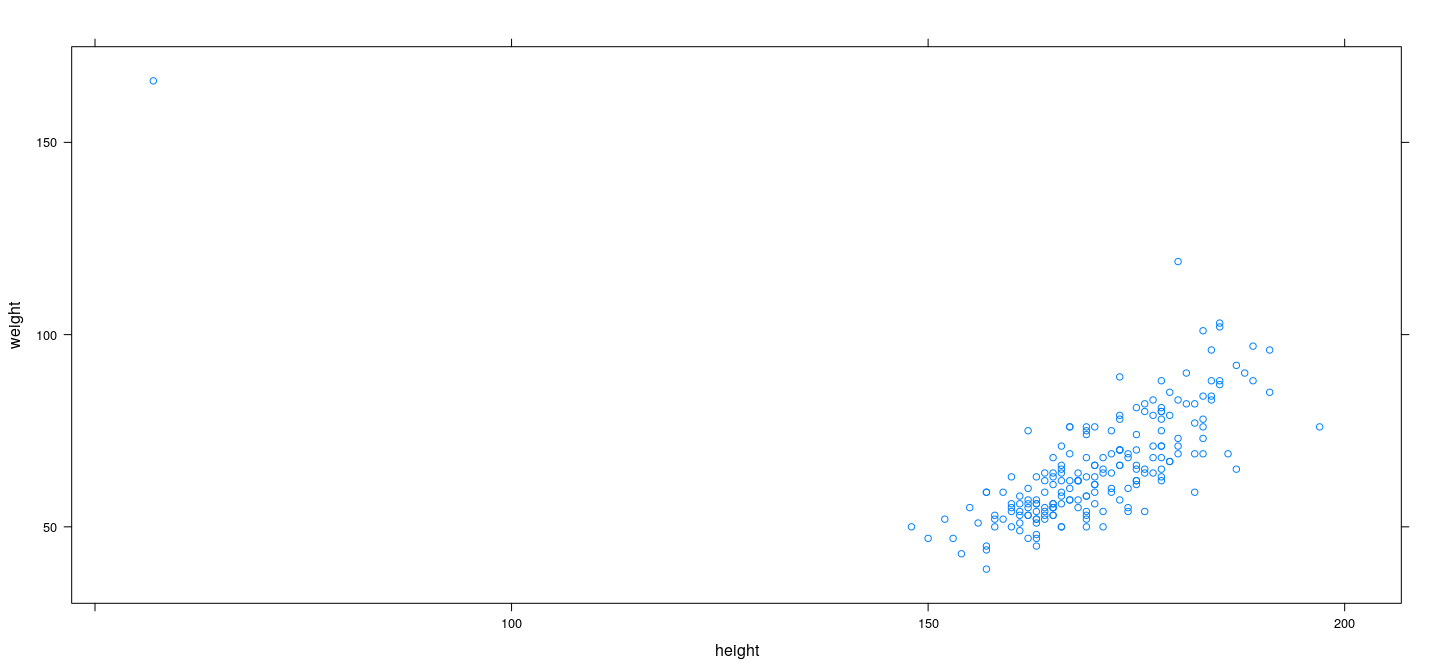
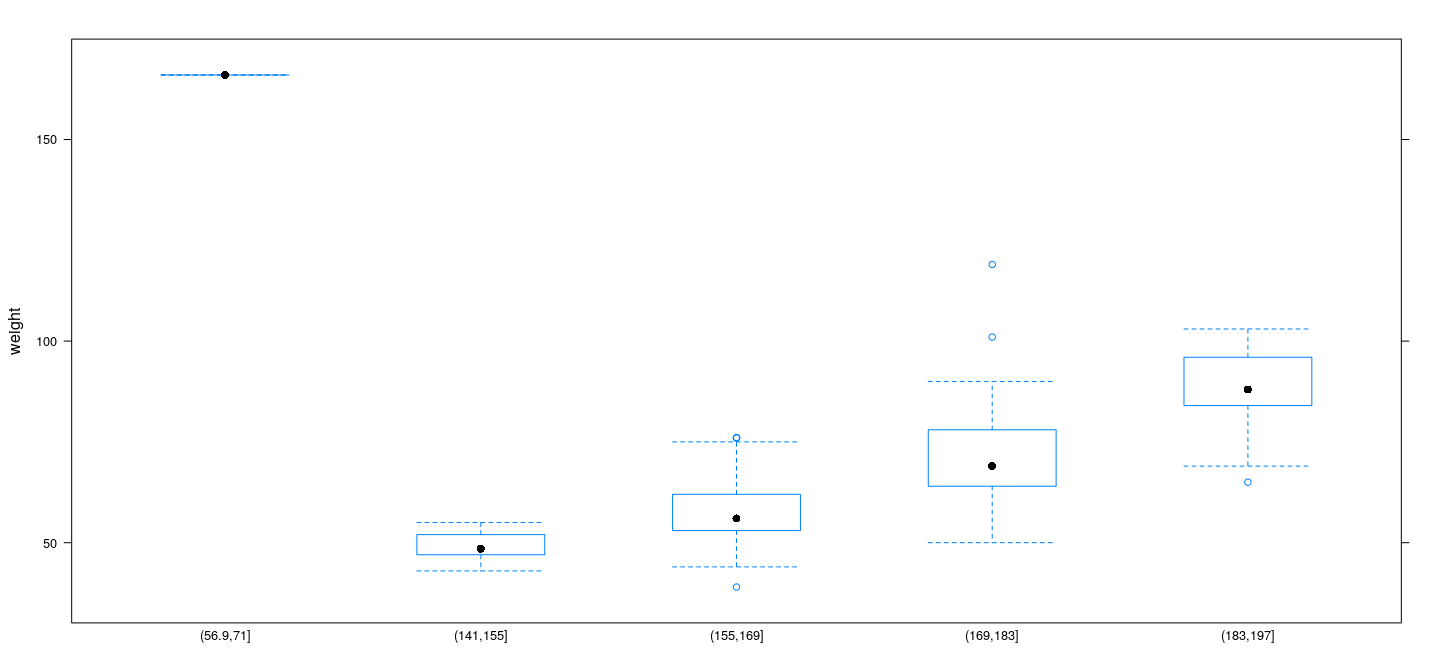
Example: Davis data
Example: UN data
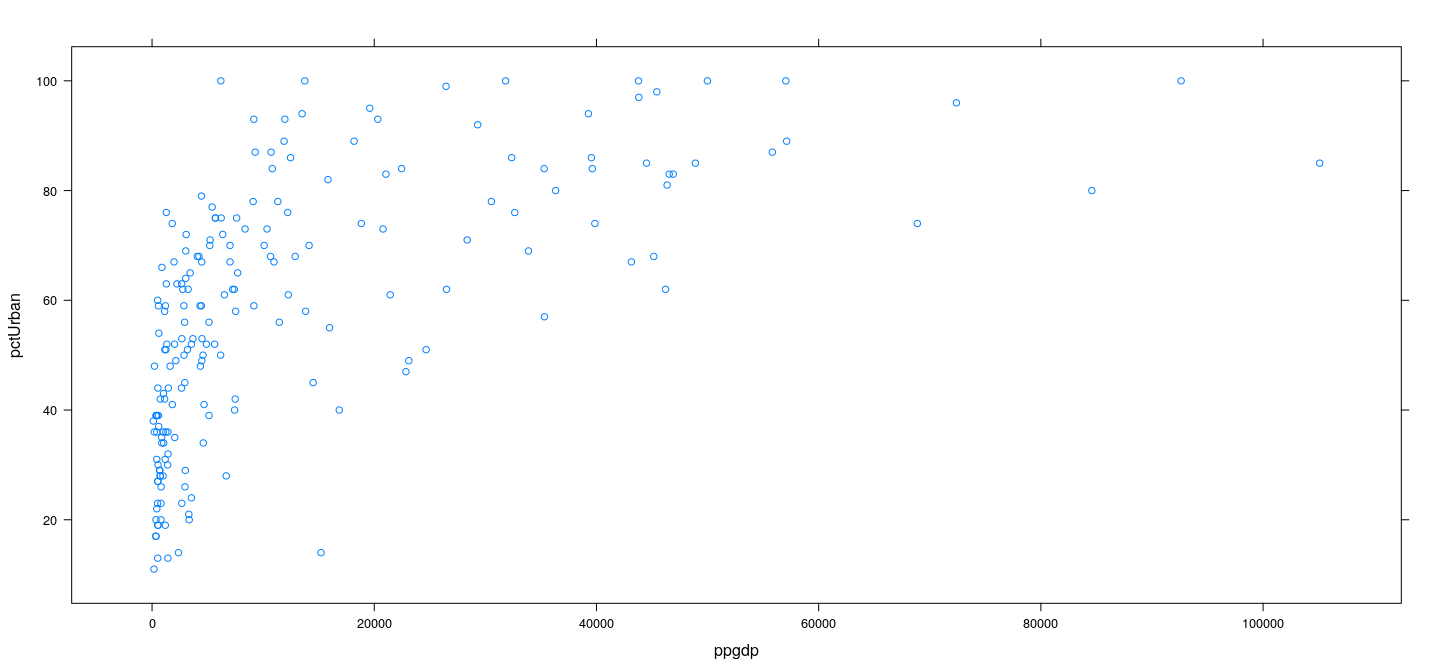
Example: UN data
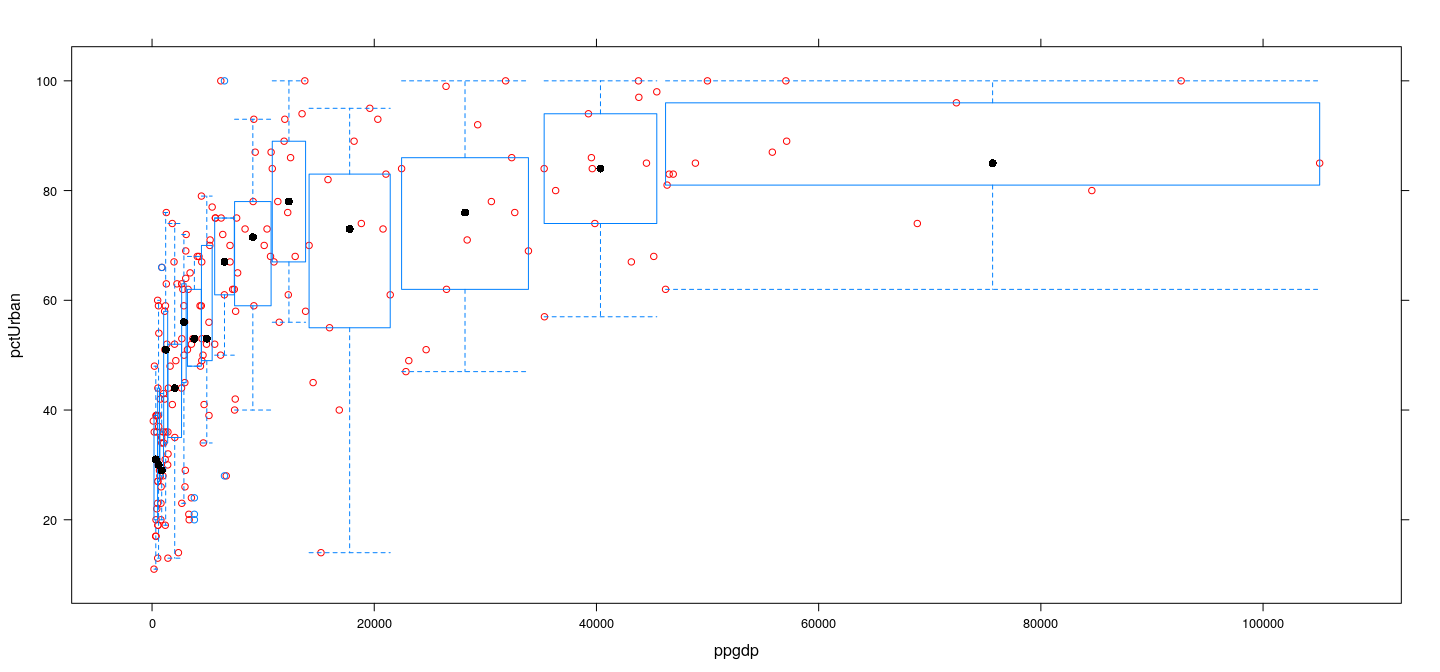
Choice of bin width - constant vs variable
Constant bin width means some bins could have very few data, or even be empty
- Generally better to define bins with fixed number of data points
- Decide number of bins
- Bin boundaries are defined by quantiles
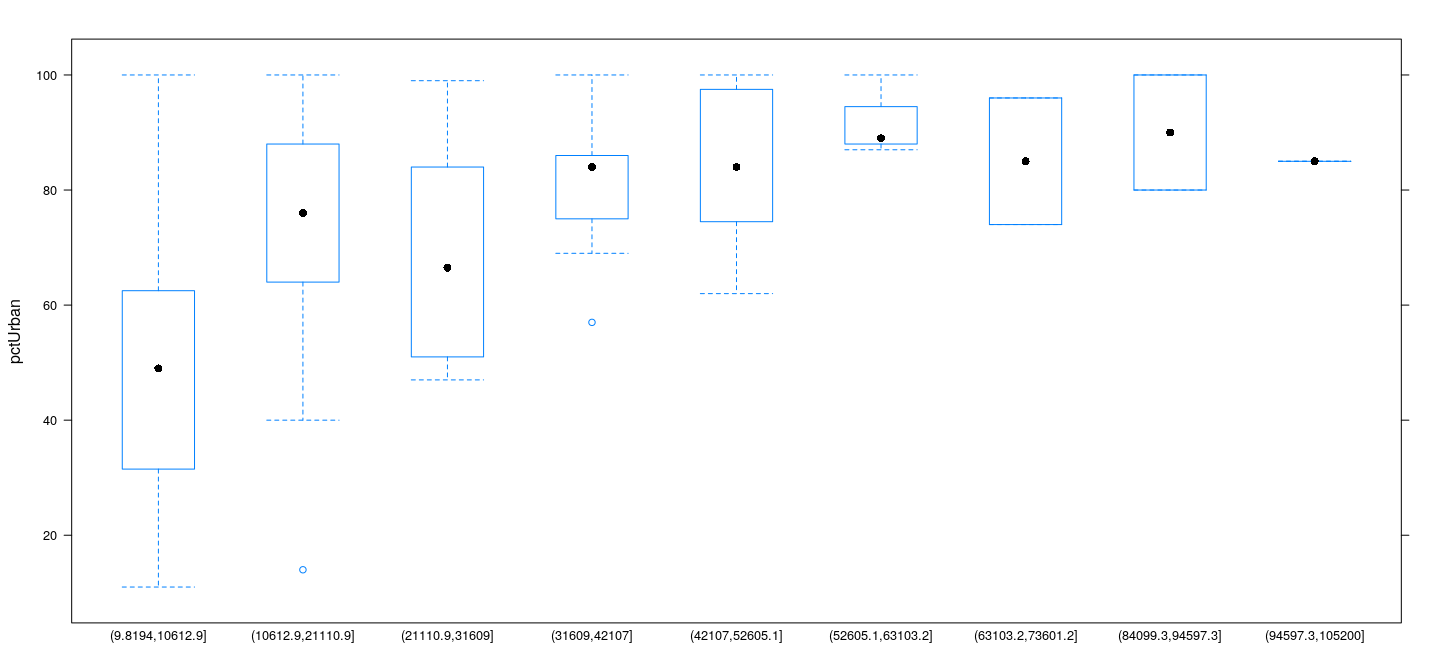
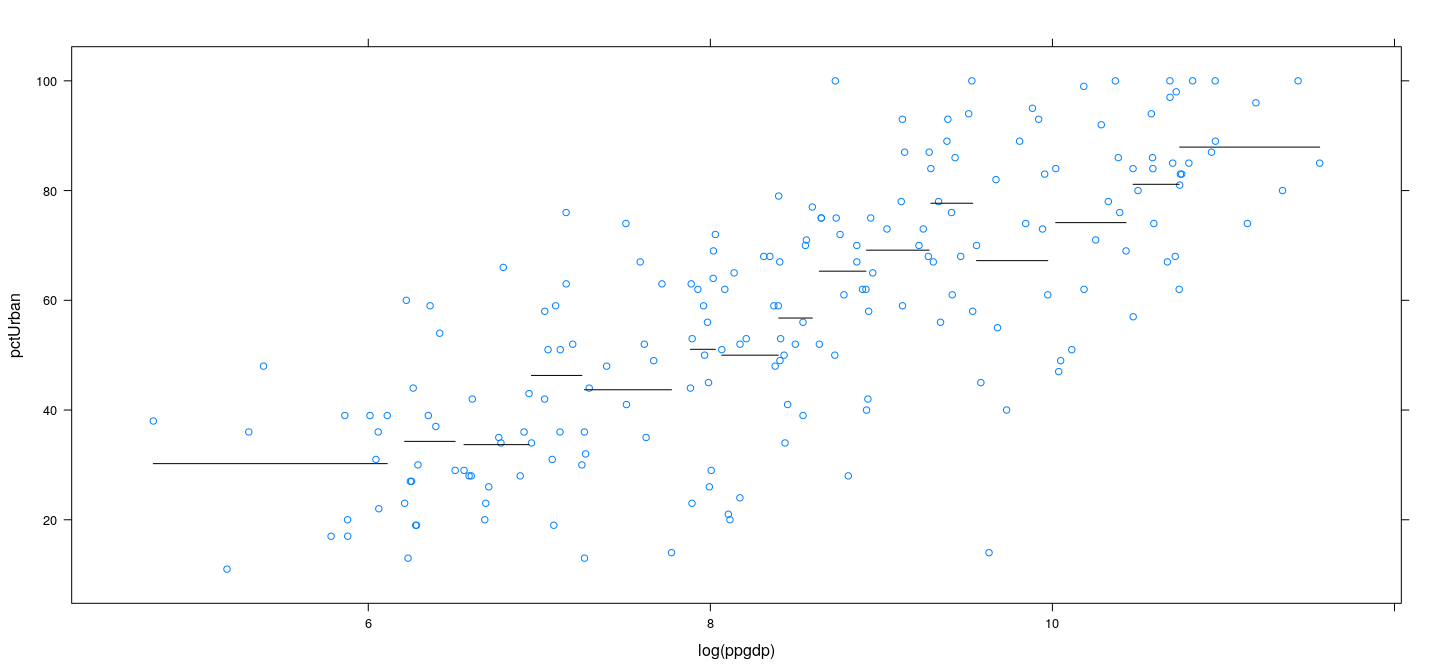
Example: UN data — box and whisker plots
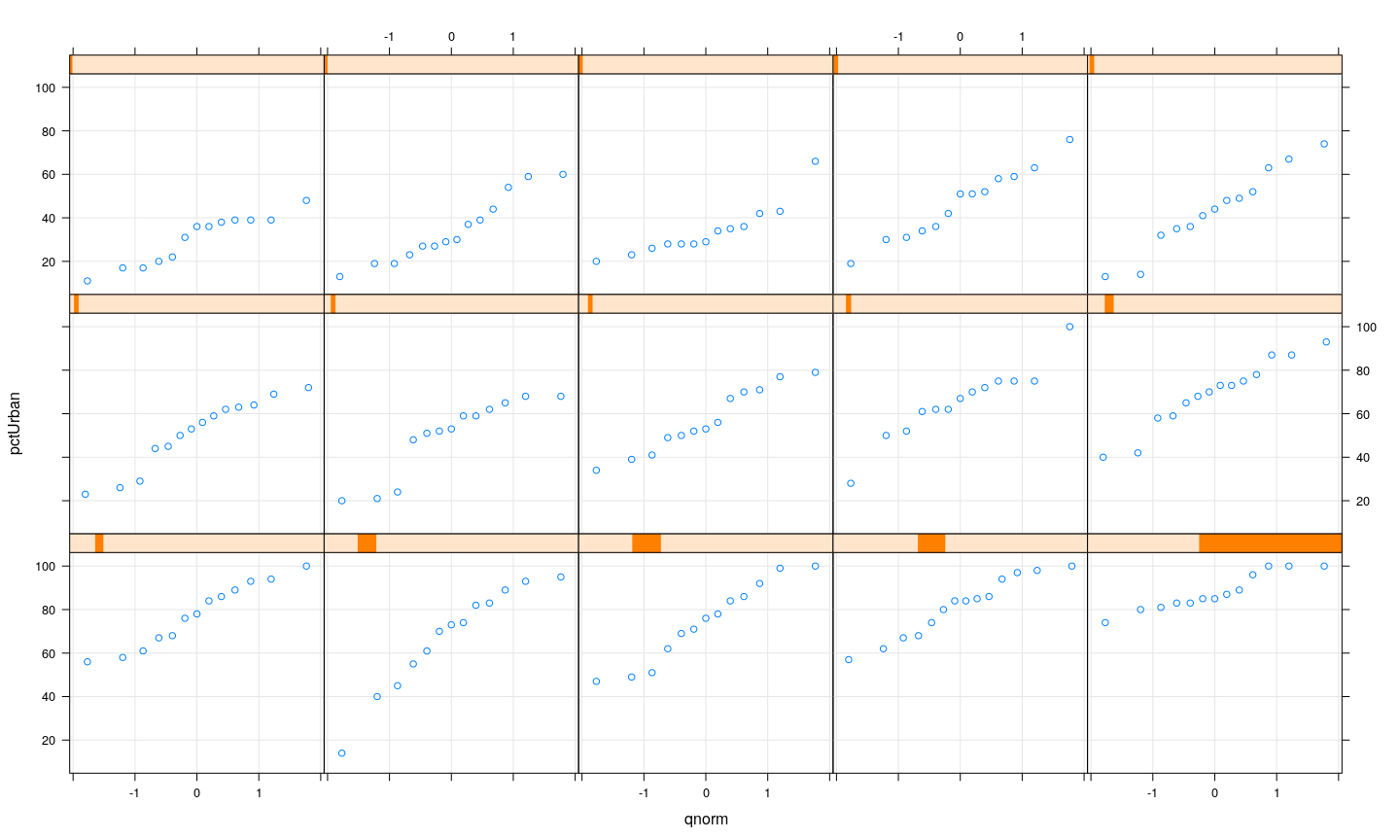
Example: UN data — Q-Q plots
Example: UN data — log-transformed GDP
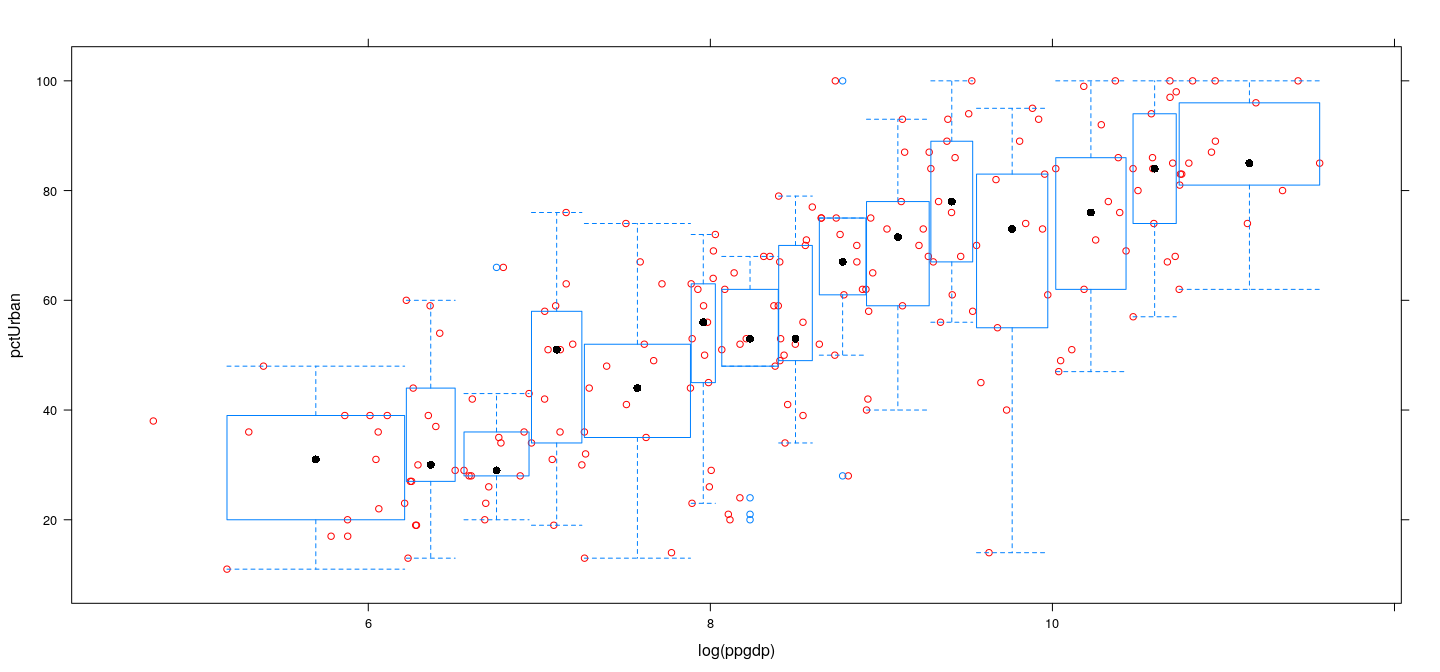
Assessing linearity
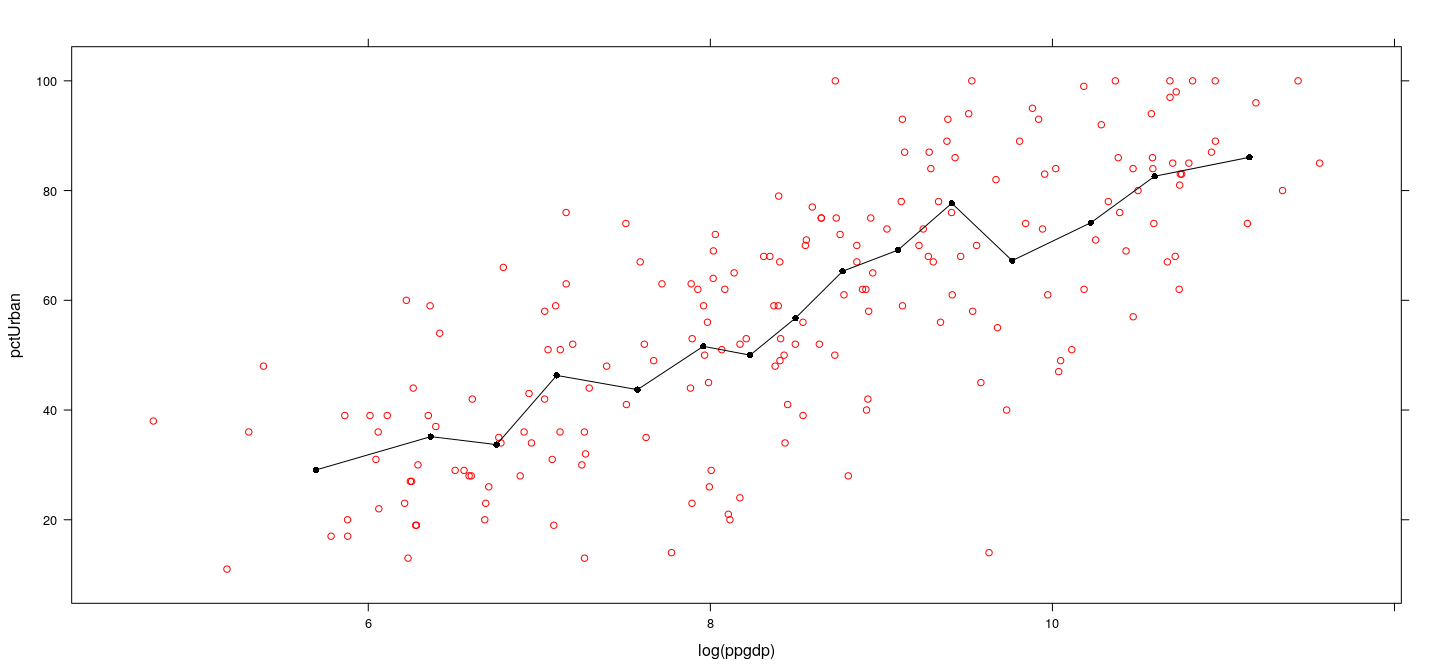
- Can summarize distribution in each bin my mean or median (and possibly standard deviation to assess non-constant variance)
Estimating conditional mean: a local binning approach
Model: \(Y_i = f(x_i) + \varepsilon_i\)
Interested in estimating \(f(x) = E(Y|x)\) for various \(x\)
Approach: Estimate \(f(x)\) locally by fitting mean or linear regression within bin
- Window size represents trade-off
- Larger window means more data points
- More data points means lower variance
- But larger window means larger bias
- Specifically, estimate is biased if \(f\) is non-linear, or if \(x\) is not uniformly distributed
Bias-variance trade-off — large data
Any reasonable method should at least be consistent
In other words, if we want to estimate \(E(Y|x)\), we should have \[ \hat{E}_n(Y|x) \to E(Y|x) \text{ as } n \to \infty \]
Suppose for sample size \(n\), we define \(\sqrt{n}\) bins, each containing \(\sqrt{n}\) points.
- Clearly, as \(n \to \infty\),
- number of bins \(\to \infty\)
- width of each bin \(\to 0\) (with some assumptions about \(x\))
- number of data points in each bin \(\to \infty\)
Bias-variance trade-off — large data
If \(f(x) = E(Y | x)\) is “smooth”, then for \(x_i\) in the same bin as \(x_0\),
\[ f(x_i) = f(x_0) + f'(x_0) (x_i - x_0) + h(x_i) (x_i - x_0) \]
where \(h(\cdot)\) is such that \(\lim_{x\to x_0} h(x) = 0\) (Taylor’s Theorem)
\(Y_i = f(x_i) + \varepsilon_i\), so for \(x_i\) in the same bin as \(x_0\), \[ Y_i = f(x_0) + f'(x_0) (x_i - x_0) + h(x_i) (x_i - x_0) + \varepsilon_i \]
and so
\[ \bar{Y} (x_0) = f(x_0) + f'(x_0) (\bar{x} - x_0) + \bar{\varepsilon} + \frac{1}{n} \sum_i h(x_i) (x_i - x_0) \]
As \(n \to \infty\), \(x_i, \bar{x} \to x_0\), so \(\bar{Y} (x_0) \to f(x_0)\)
Example: UN data
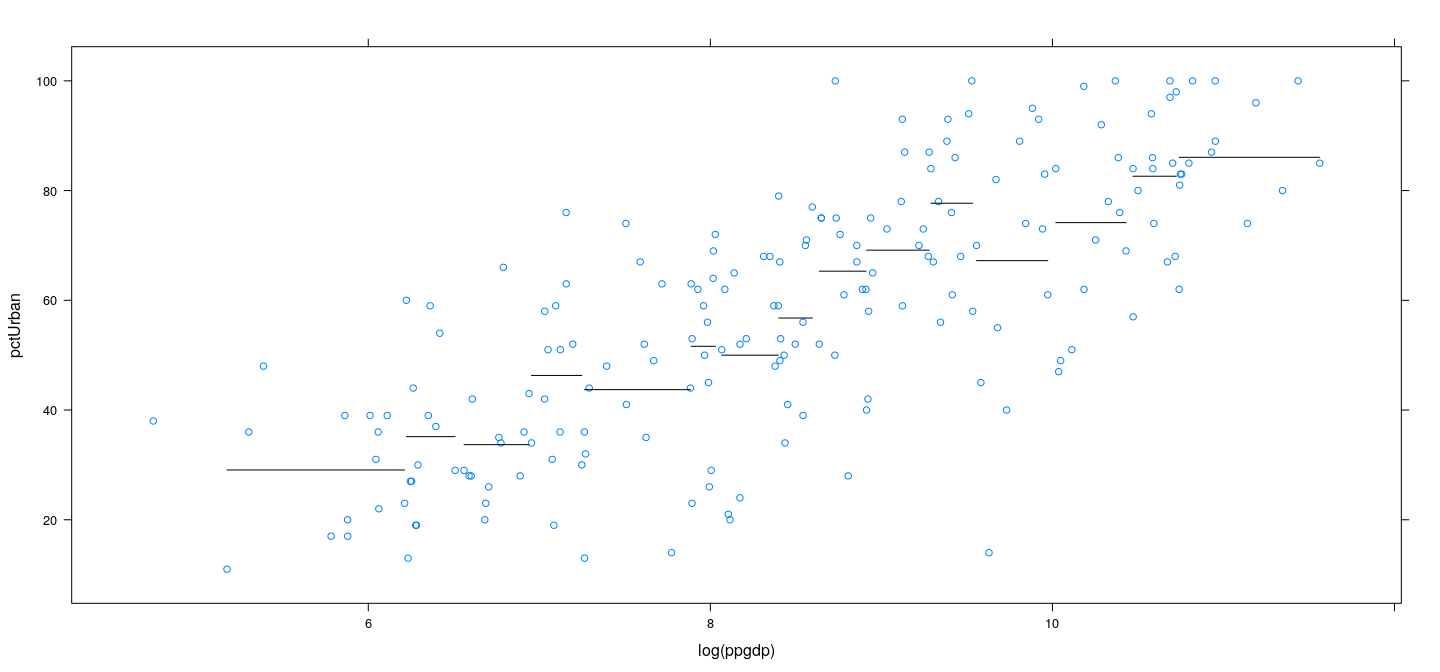
Example: UN data – overlapping bins
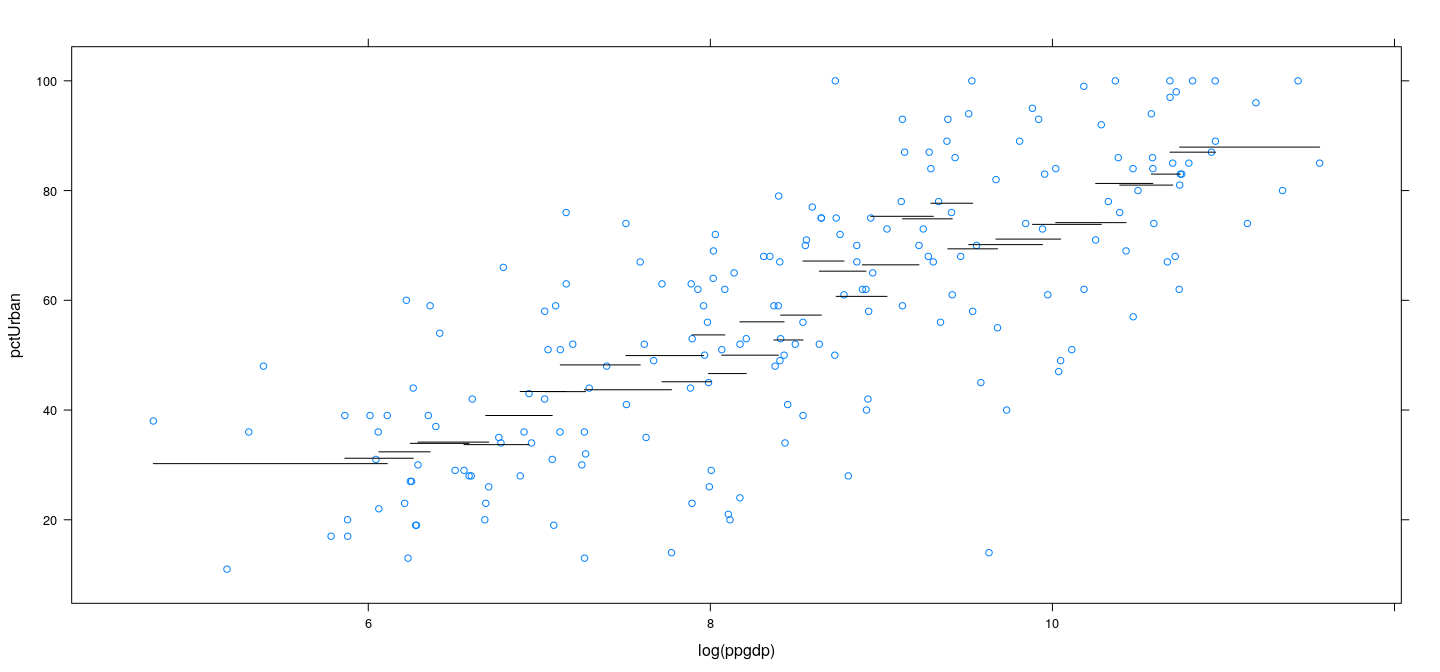
Example: UN data – overlapping bins
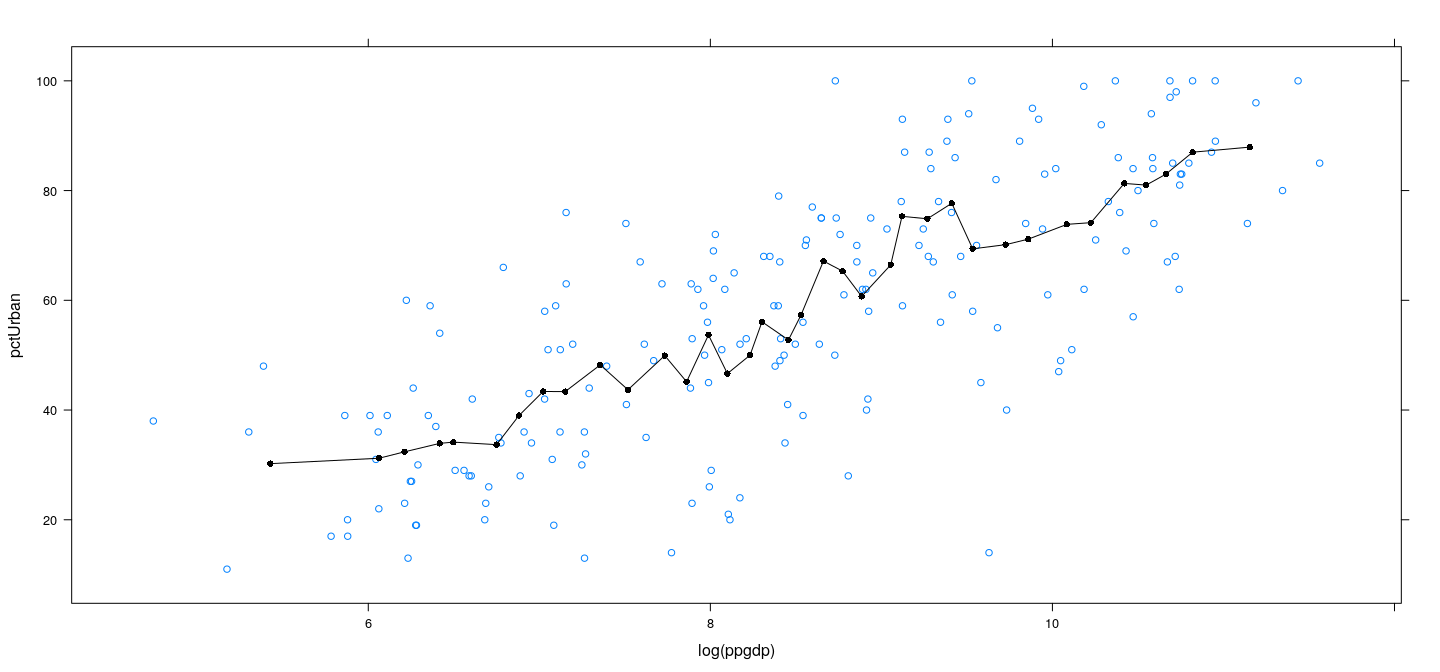
Example: UN data – more bins
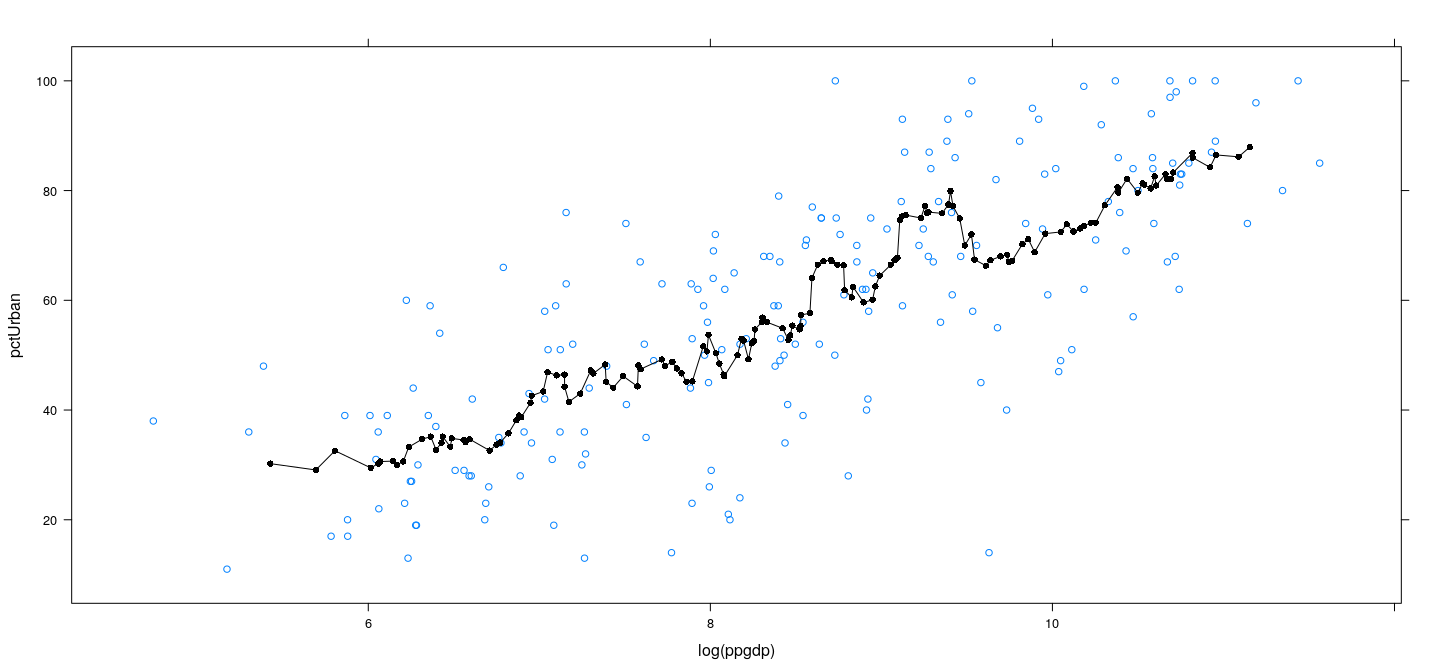
Example: UN data – wider bins
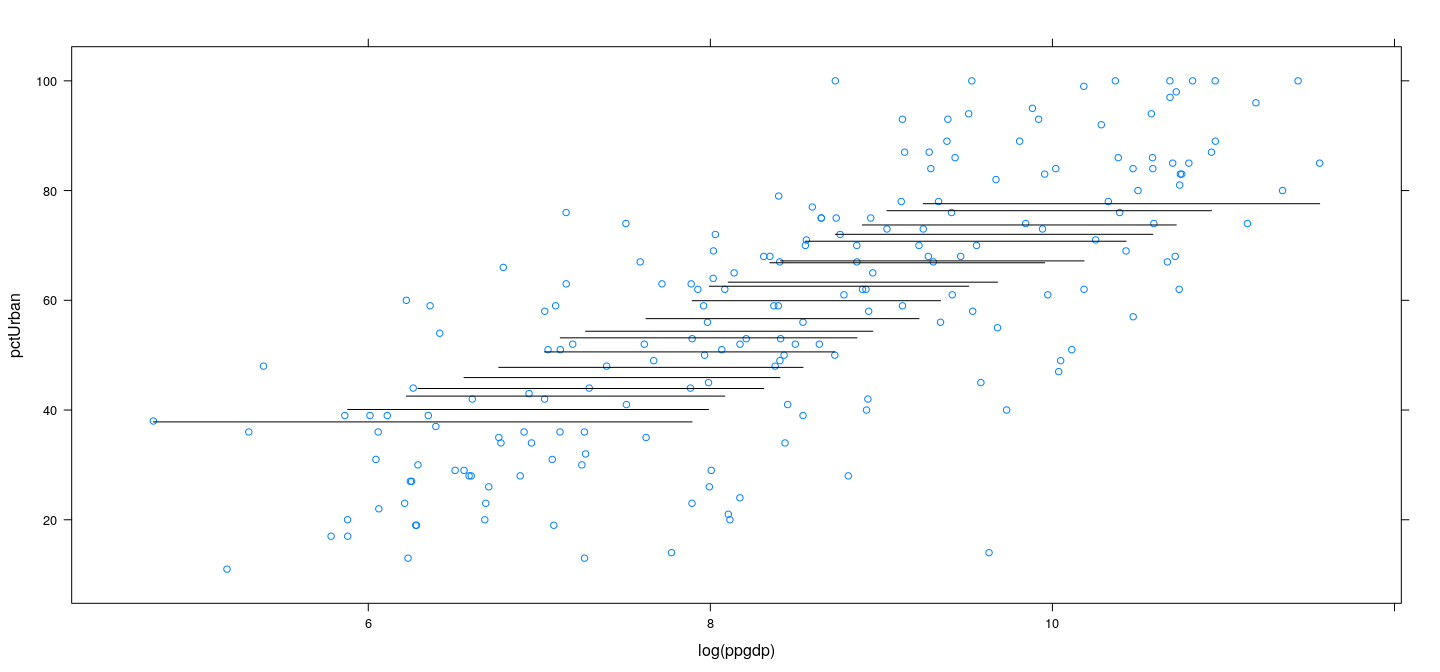
Example: UN data – wider bins
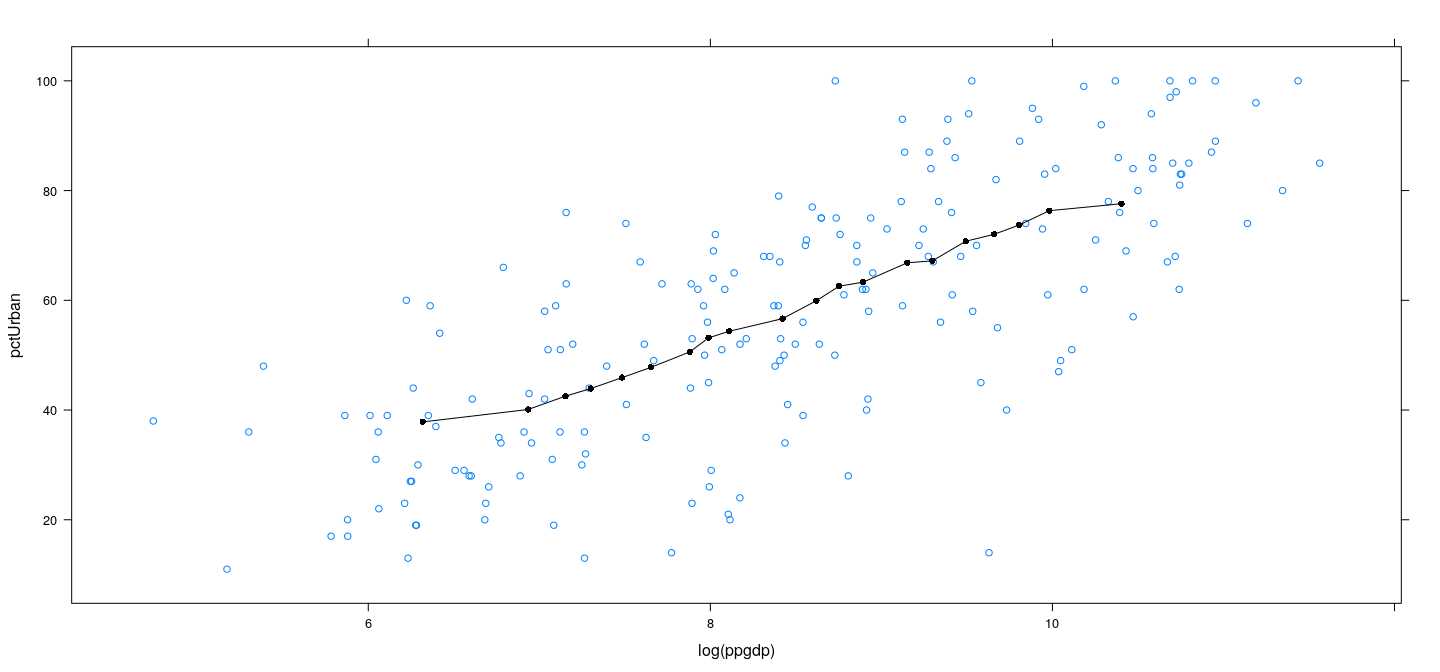
Locally linear regression
Instead of \(\bar{Y}\), we could fit a linear regression model in each bin
\[ \hat{Y} (x_0) = \hat\alpha \]
where \(\hat\alpha\) and \(\hat\beta\) are estimated by fitting the linear regression model (for all \(x_i\) in the same bin as \(x_0\))
\[ Y_i = \alpha + \beta (x_i - x_0) + \varepsilon_i \]
- In general, the model could be a \(d\)-th “degree” polynomial
- \(d = 0\) : local mean
- \(d = 1\) : locally linear fit
- \(d = 2\) : locally quadratic fit
- Tuning parameter “span” : proportion of full data in each bin
Example: UN data – locally linear
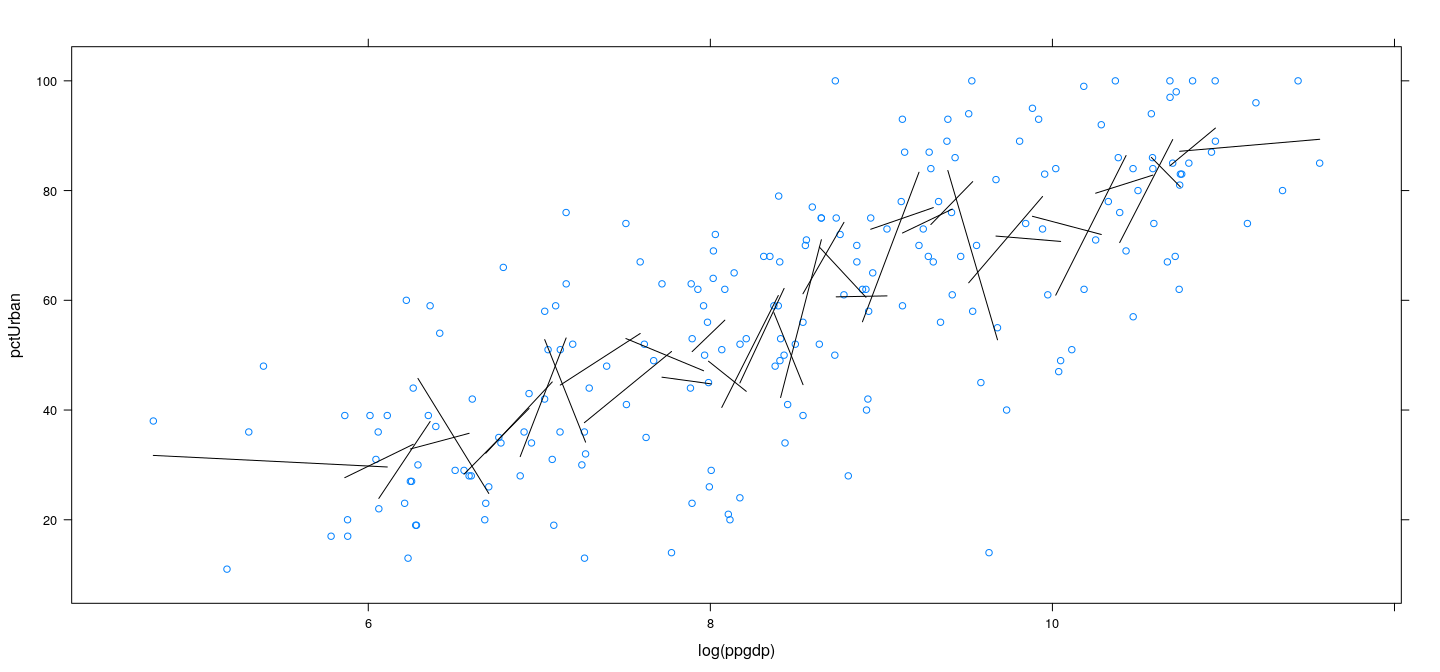
Example: UN data – locally linear
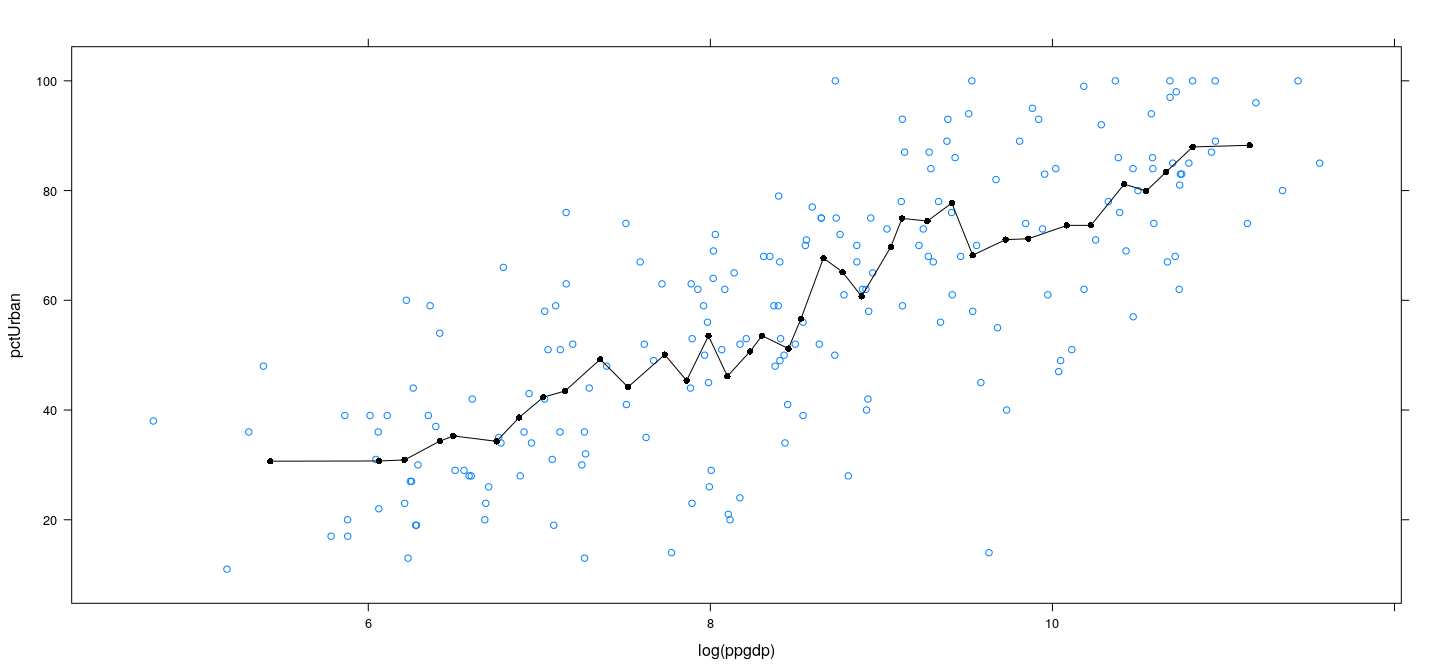
Example: UN data – locally linear with more bins
Example: UN data – locally linear with more bins
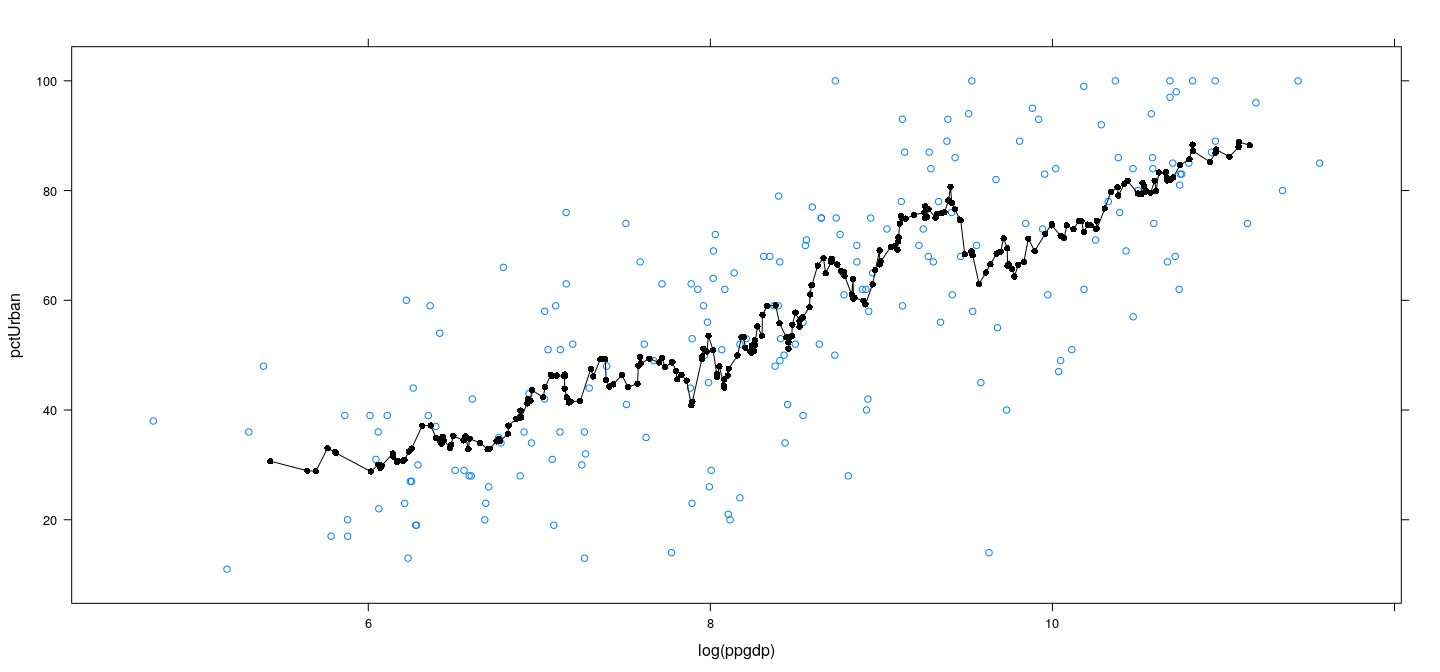
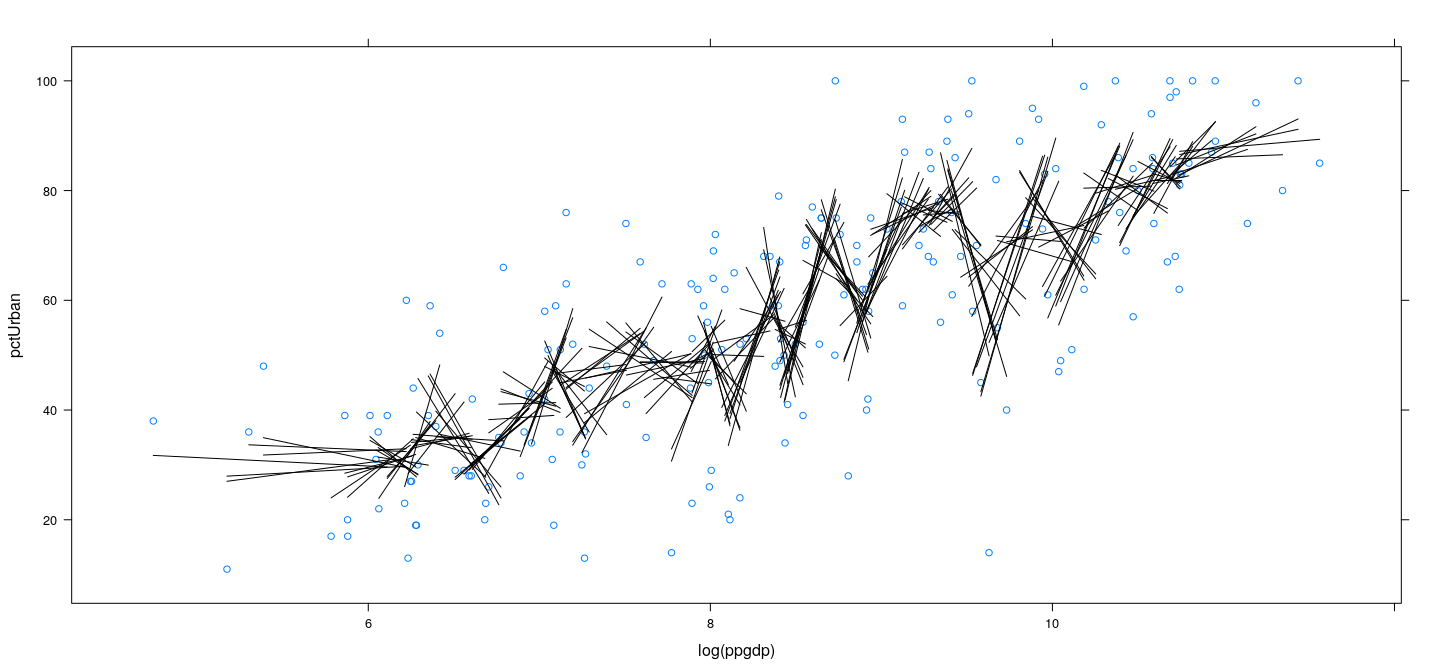
Example: UN data – locally linear with wider bins
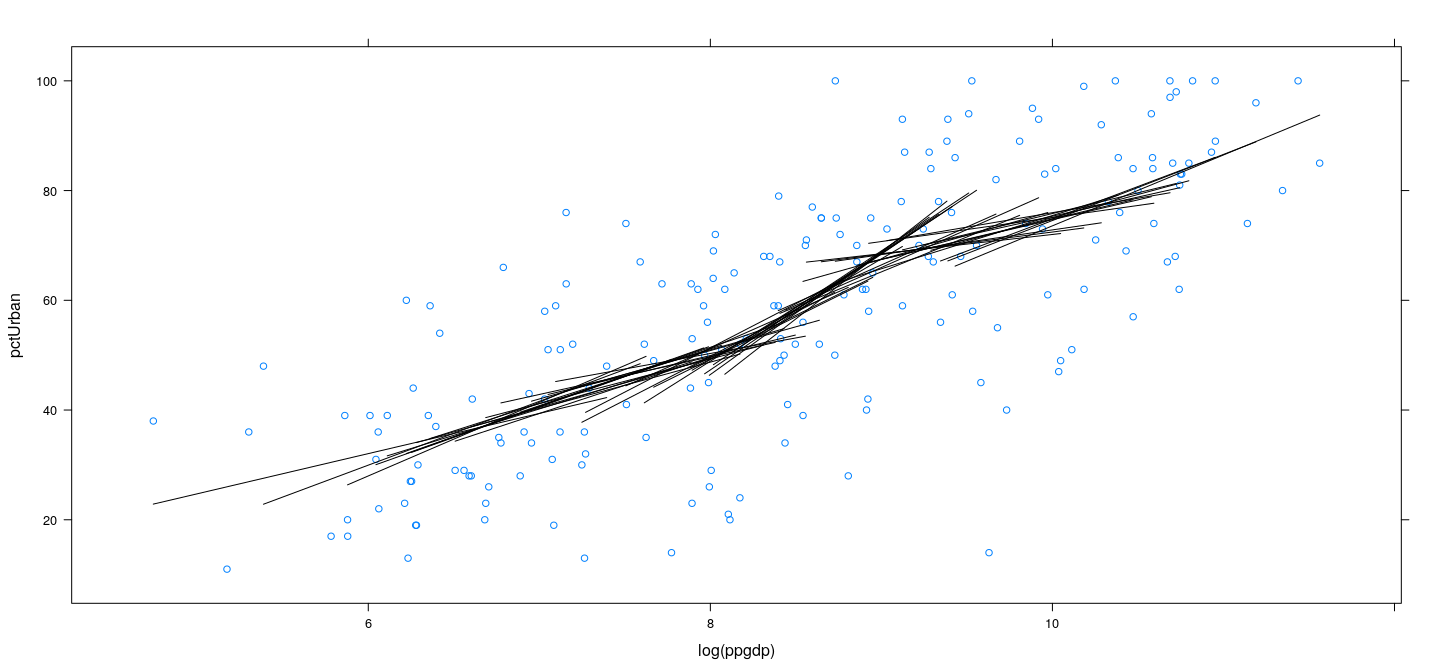
Example: UN data – locally linear with wider bins
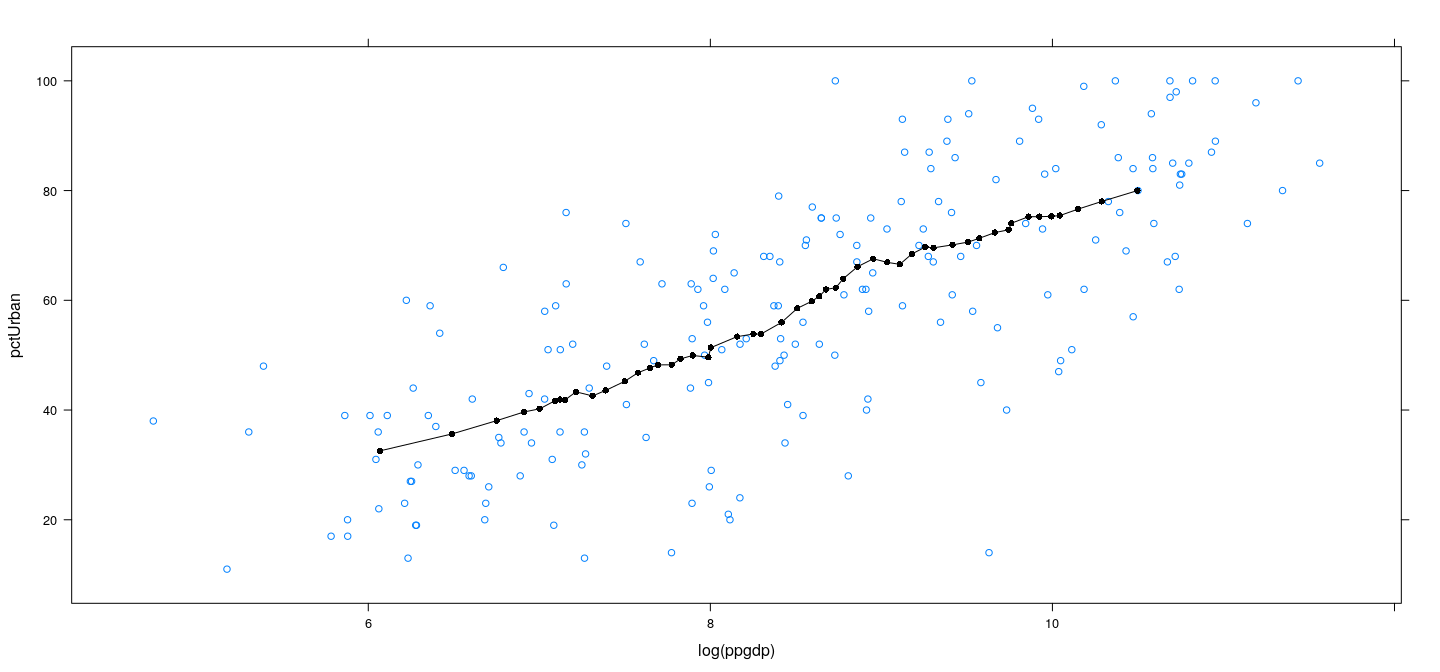
Adding weights
- Larger span gives
- Wider bins
- Smoother estimate of \(f(x) = E(Y|x)\)
- But more data points per bin (less “local”)
- One solution is to add weights (give more weightage to \(x_i\) near \(x_0\))
Weighted mean: \(\hat{Y} = \frac{\sum w_i Y_i}{ \sum w_i }\)
Weighted regression: Normal equations are given by \[ \mathbf{X}^T \mathbf{W} \mathbf{X} \widehat{\beta} = \mathbf{X}^T \mathbf{W} \mathbf{y} \] where \(\mathbf{W}^{-1}\) is a diagonal matrix of inverse weights \(1/w_i^2\) (higher weight means less uncertainty).
- For example, \[
w_i = k((x_i - x_0) / h),
\] where
- \(2h\) is the bin width
- \(k(\cdot)\) is a symmetric weight function that is highest at \(0\) and decreases (usually to \(0\) at \(\pm h\))
Example: UN data – locally weighted linear regression
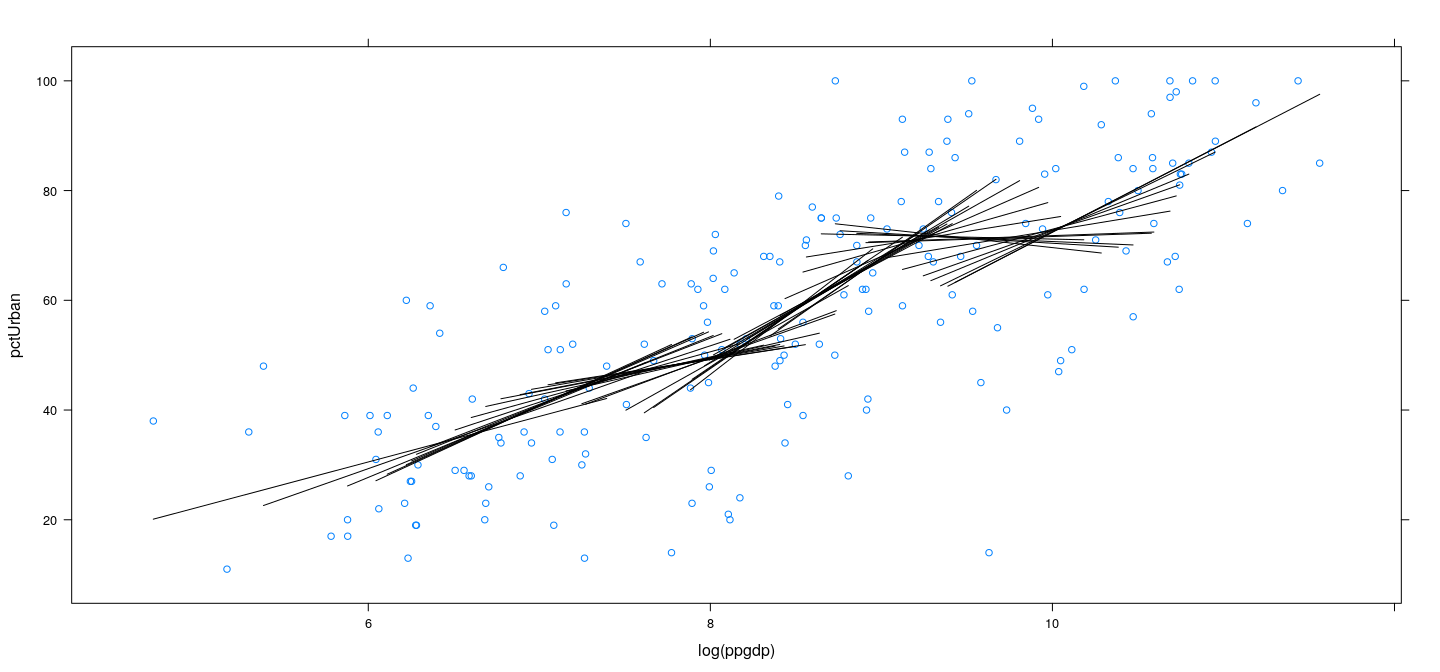
Example: UN data – locally weighted linear regression
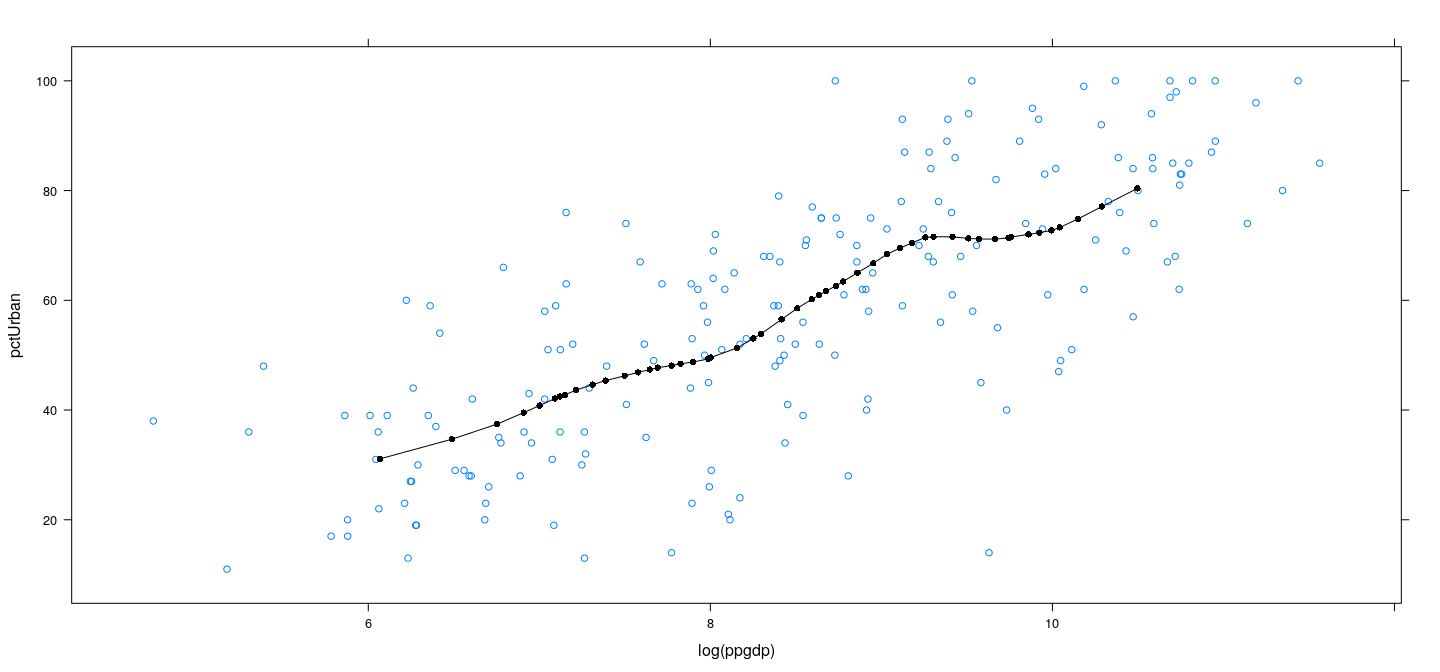
Example: UN data – LOWESS
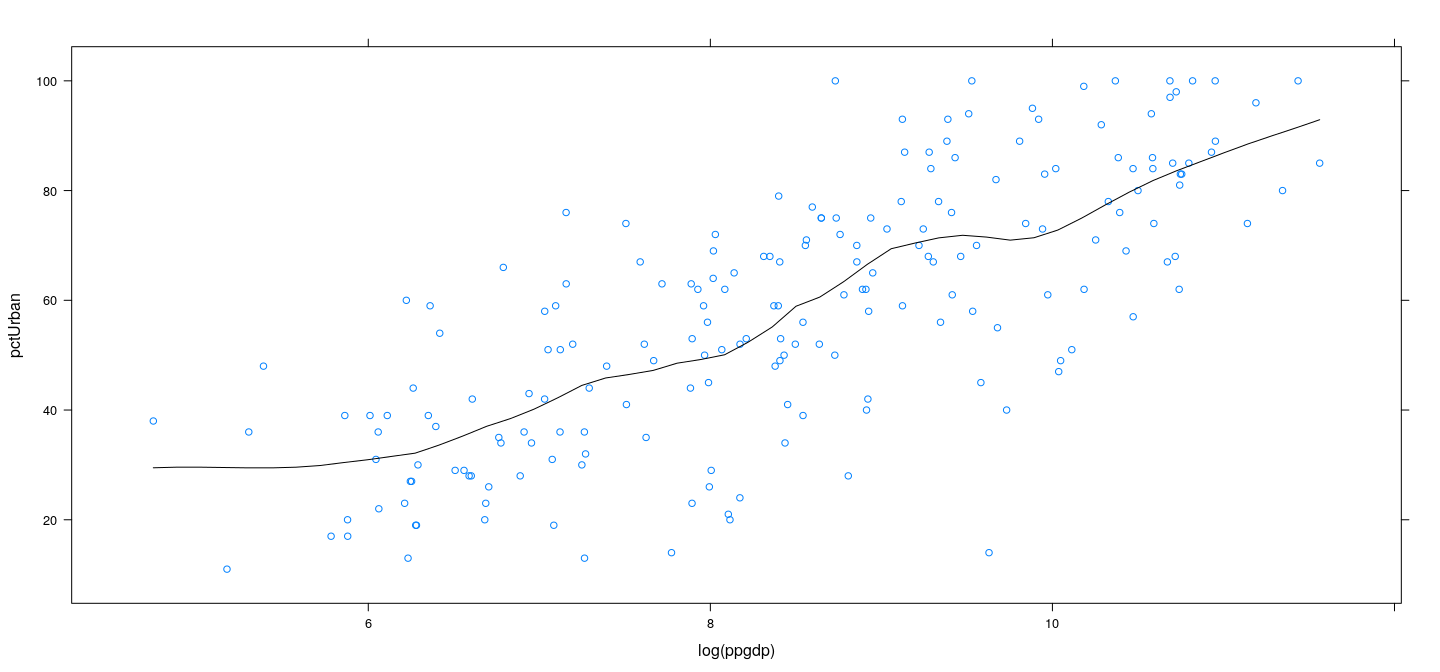
LOWESS
Stands for “LOcally WEighted Scatterplot Smoother”
Can be viewed as \(k\) nearest neighbour weighted local polynomial regression
Main control parameters are
spananddegree
Optionally provides estimates of standard error
By default also provides “robust” estimates
Example: UN data – LOWESS
xyplot(pctUrban ~ log(ppgdp), data = UN, type = c("p", "smooth"),
span = 0.27, degree = 1, family = "gaussian")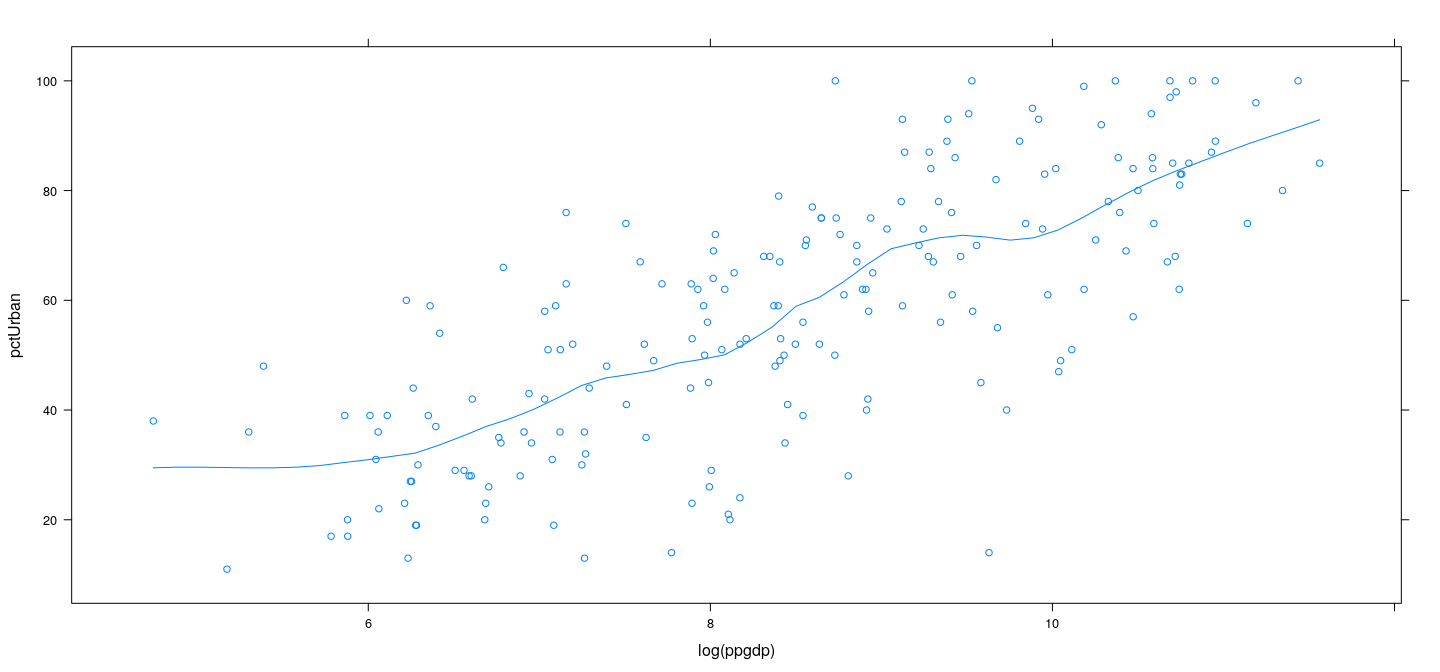
Example: UN data – LOWESS
xyplot(pctUrban ~ log(ppgdp), data = UN, type = c("p", "smooth"),
span = 2/3, degree = 2, family = "gaussian")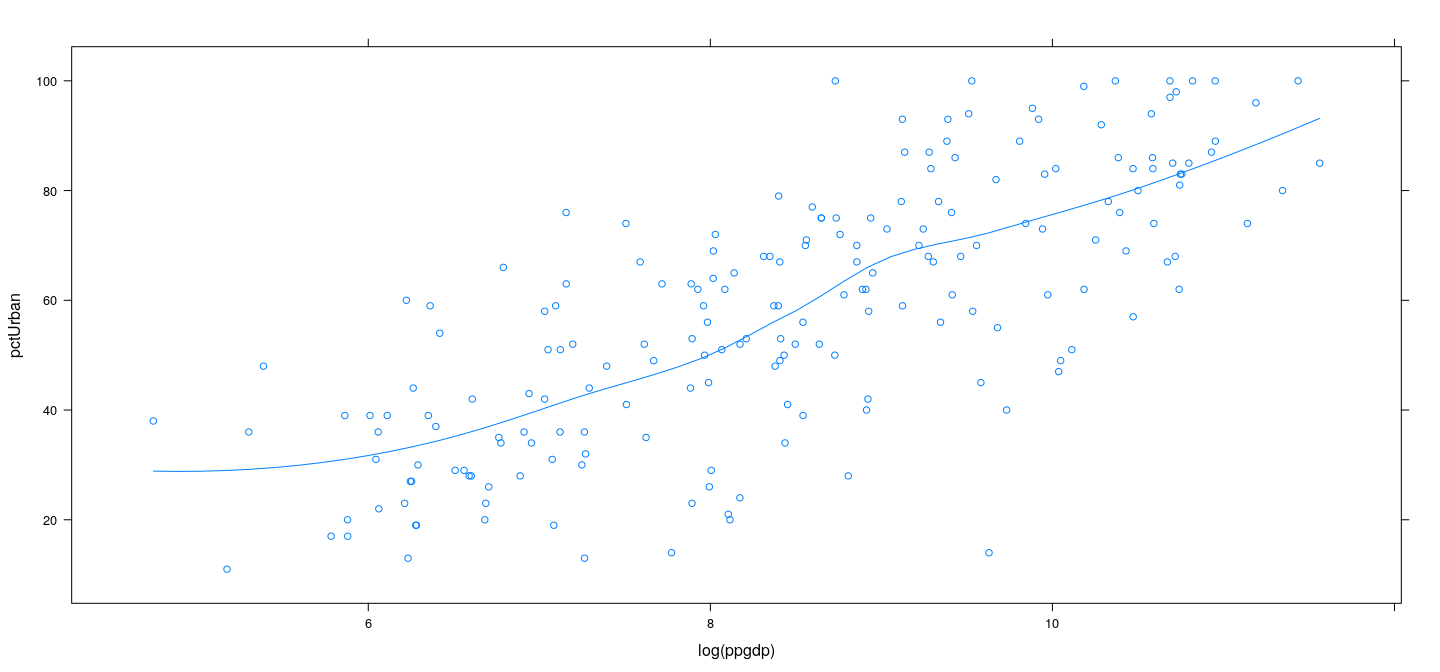
Example: UN data – LOWESS
xyplot(pctUrban ~ log(ppgdp), data = UN, type = c("p", "smooth"),
span = 2/3, degree = 2, family = "symmetric")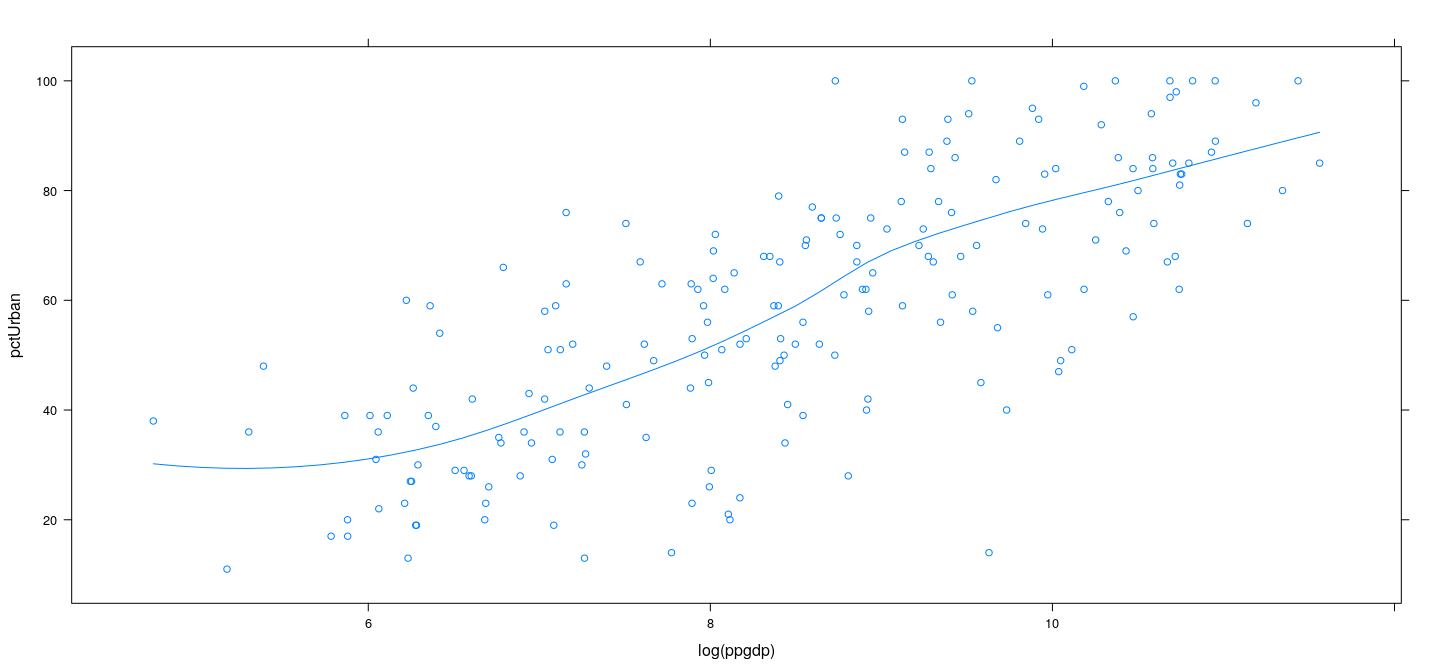
Example: UN data – LOWESS with local mean
xyplot(pctUrban ~ log(ppgdp), data = UN, type = c("p", "smooth"),
span = 2/3, degree = 0, family = "symmetric")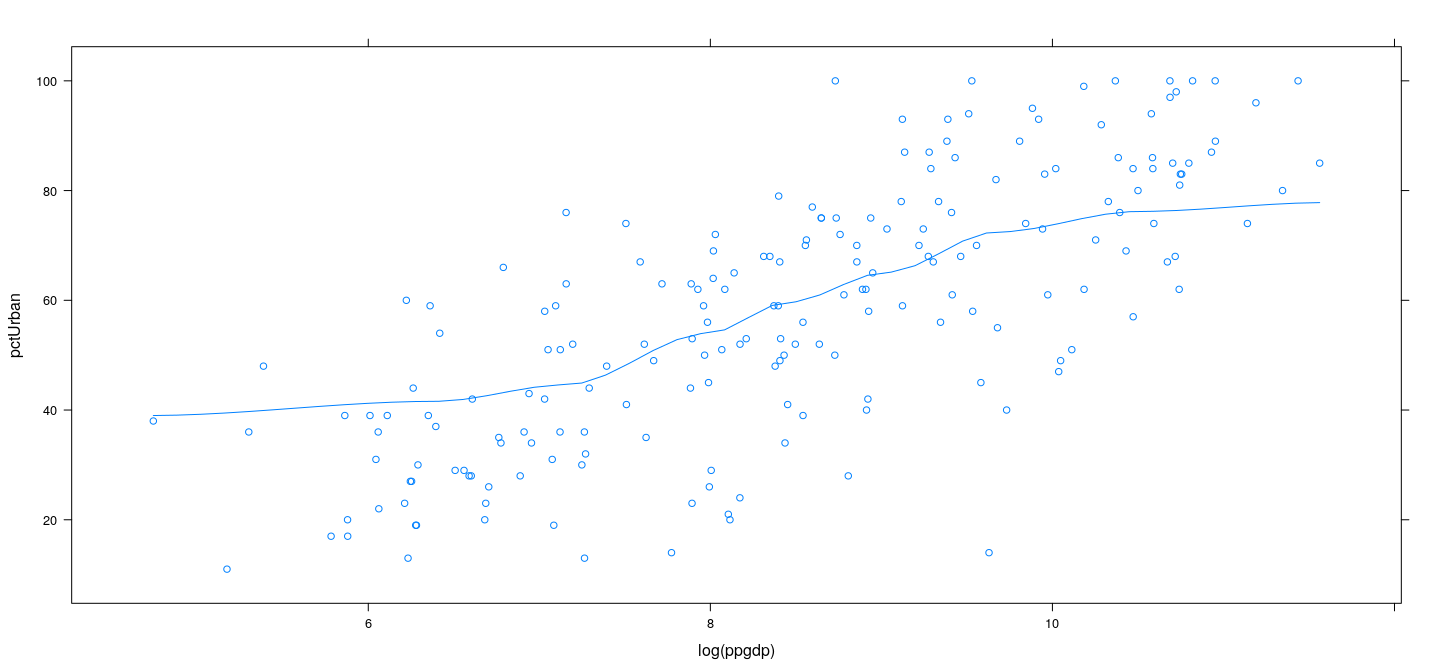
Example: UN data – LOWESS with confidence band
library(latticeExtra)
xyplot(pctUrban ~ log(ppgdp), data = UN) + layer(panel.smoother(x, y, method = "loess", se = TRUE))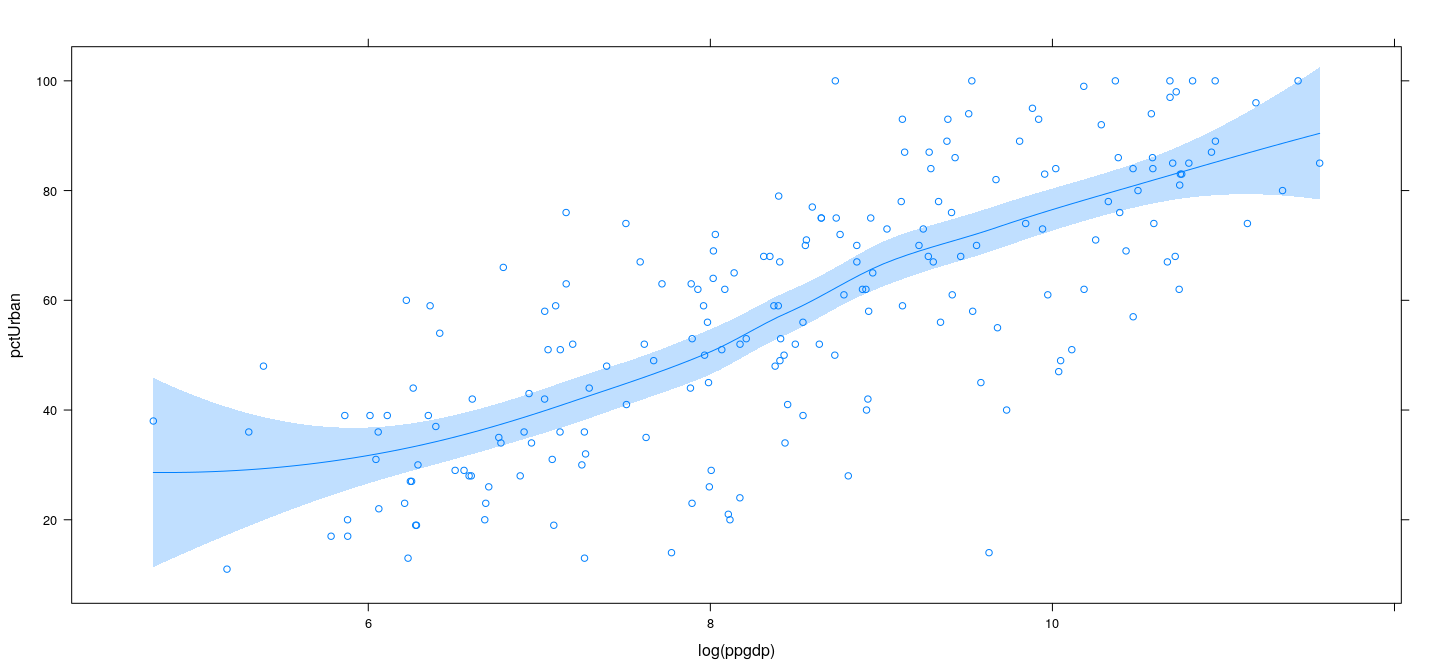
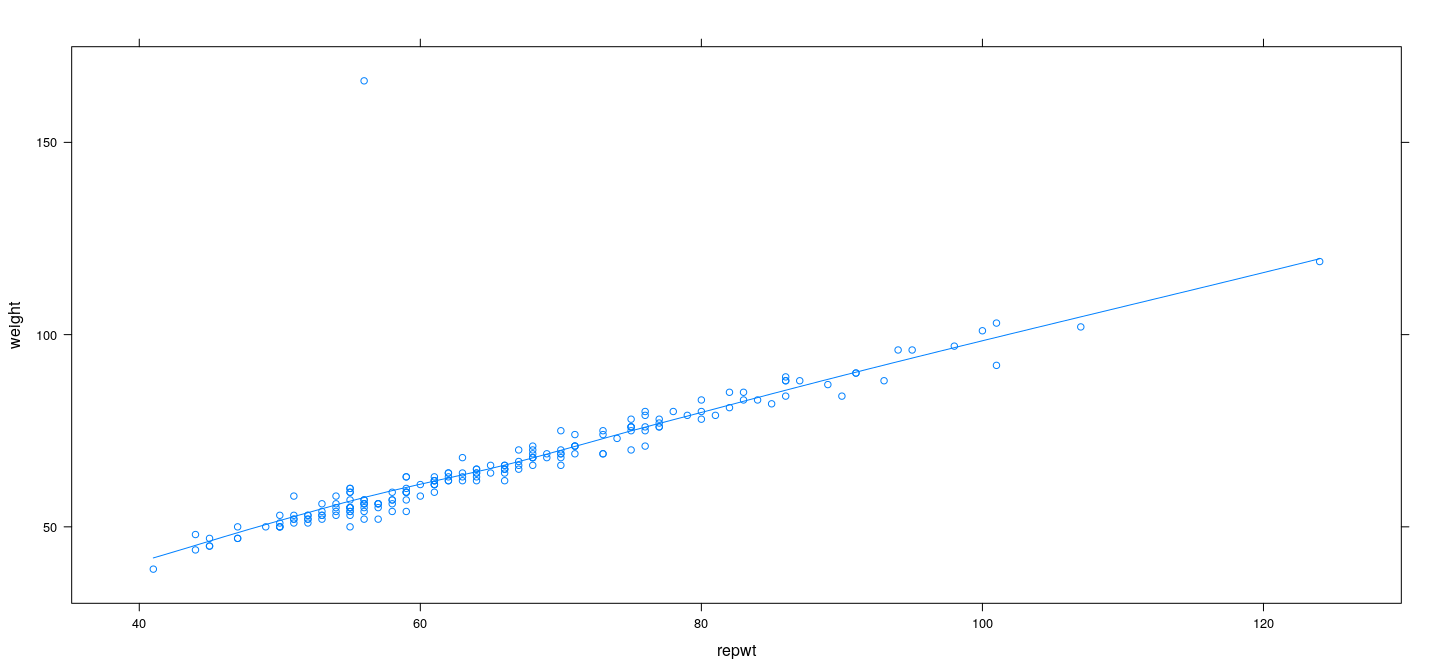
Example: Davis data – LOWESS with least squares
Example: Davis data – LOWESS with robust regression
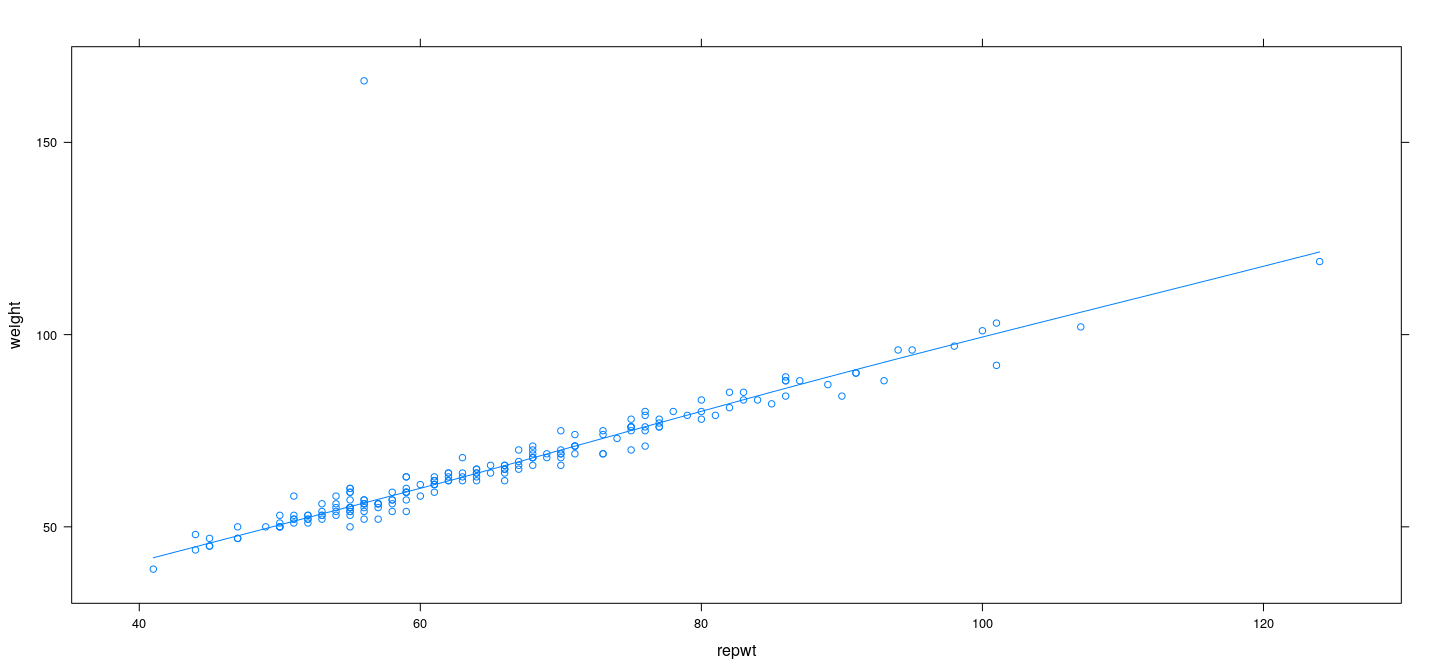
Example: Davis data – effect of span
Choice of span in LOWESS
The
span(proportion of data in each bin) is an important tuning parameterHow do we choose
span?Generally speaking, cross-validation is often a useful strategy for choosing tuning parameters
Choose
spanto minimize \[ \sum_{i=1}^n (Y_i - \hat{Y}_{i(-i)})^2 \]This is equivalent to maximixing predictive \(R^2\)
- Next assignment!
Parametric “smooth” regression
The linear model is actually more flexible than it first seems
Recall our previous example:
Parametric “smooth” regression
This can be viewed as a piecewise constant \(f(x)\)
Choose breakpoints (“knots”) \(-\infty = t_0 < t_1 < t_2 < \cdots < t_k = +\infty\)
Define \(Z_{ji} = 1\{ X_i \in (t_{j-1}, t_{j} ] \}\) for \(j = 1, 2, \dotsc, k\)
- Fit linear model \(\mathbf{y} = \mathbf{Z \beta} + \mathbf{\varepsilon}\) — this will give piecewise constant \(\hat{f}\)
Pieceise constant regression
- Implementation in R
pconst <- function(x, knots)
{
Z <- matrix(0, length(x), length(knots) - 1)
for (j in seq_len(length(knots)-1))
Z[, j] <- ifelse(knots[j] < x & x <= knots[j+1], 1, 0)
Z
}
lgdp.knots <- c(-Inf,
quantile(log(UN$ppgdp), probs = seq(0.1, 0.9, by = 0.1), na.rm = TRUE),
Inf)- Fitting a model
Pieceise constant regression
xyplot(pctUrban ~ log(ppgdp), data = UN) +
layer(panel.smoother(x, y, method = "lm", se = FALSE, n = 500, form = y ~ 0 + pconst(x, knots = lgdp.knots)))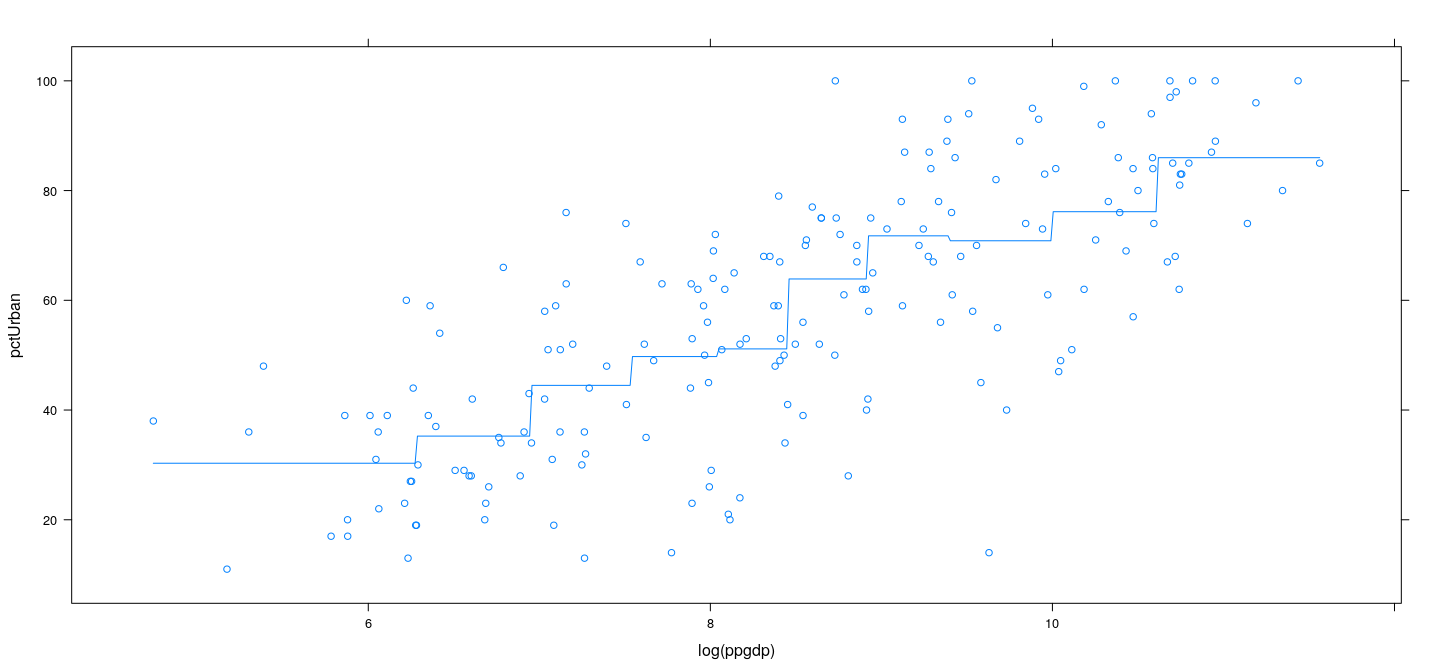
Piecewise linear regression
Knots \(-\infty = t_0 < t_1 < t_2 < \cdots < t_k = +\infty\)
\(f(x) = \alpha_j + \beta_j x\) for \(x \in (t_{j-1}, t_{j} ]\) for \(j = 1, 2, \dotsc, k\)
Define \(Z_{ji} = 1\{ X_i \in (t_{j-1}, t_{j} ] \}\) for \(j = 1, 2, \dotsc, k\)
Additionally, define \(\tilde{Z}_{ji} = Z_{ji} x_i\) for \(j = 1, 2, \dotsc, k\)
Piecewise linear regression
xyplot(pctUrban ~ log(ppgdp), data = UN) +
layer(panel.smoother(x, y, method = "lm", se = FALSE, n = 500, form = y ~ 0 + plinear(x, knots = lgdp.knots)))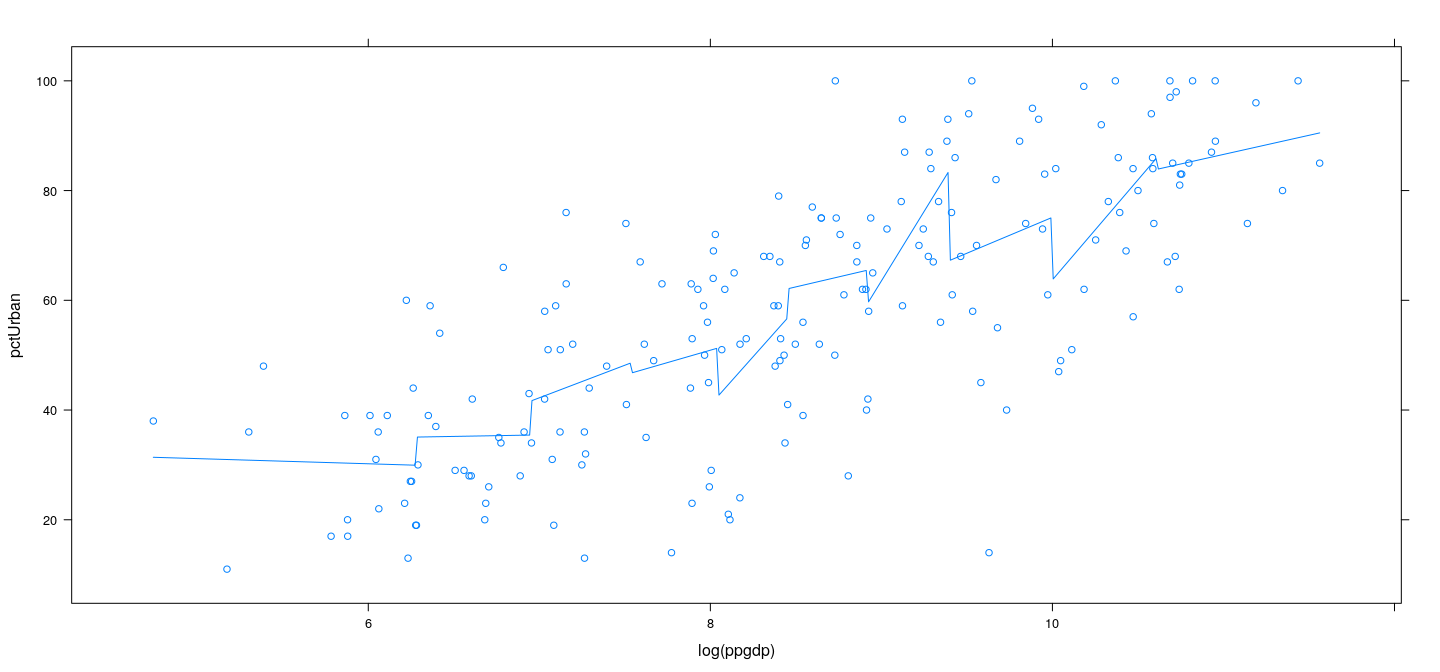
Piecewise linear interpolating regression
This is the best (least squares) piecewise linear \(f(x)\) of the form \[ f(x) = \alpha_j + \beta_j x \] for \(x \in (t_{j-1}, t_{j} ]\,,\, j = 1, 2, \dotsc, k\).
But we would prefer \(f\) to be continuous
Requires \(\alpha_j + \beta_j t_j = \alpha_{j+1} + \beta_{j+1} t_j\) for \(j = 1, 2, \dotsc, k-1\)
Equivalent formulation
\[ f(x) = \delta_0 + \gamma_0 x + \sum_{j=1}^{k-1} \gamma_j (x-t_j)_{+} \]
where \(x_{+} = \max\{ 0, x \}\)
Piecewise linear regression
xyplot(pctUrban ~ log(ppgdp), data = UN) +
layer(panel.smoother(x, y, method = "lm", se = FALSE, n = 500, form = y ~ 1 + plincont(x, knots = lgdp.knots)))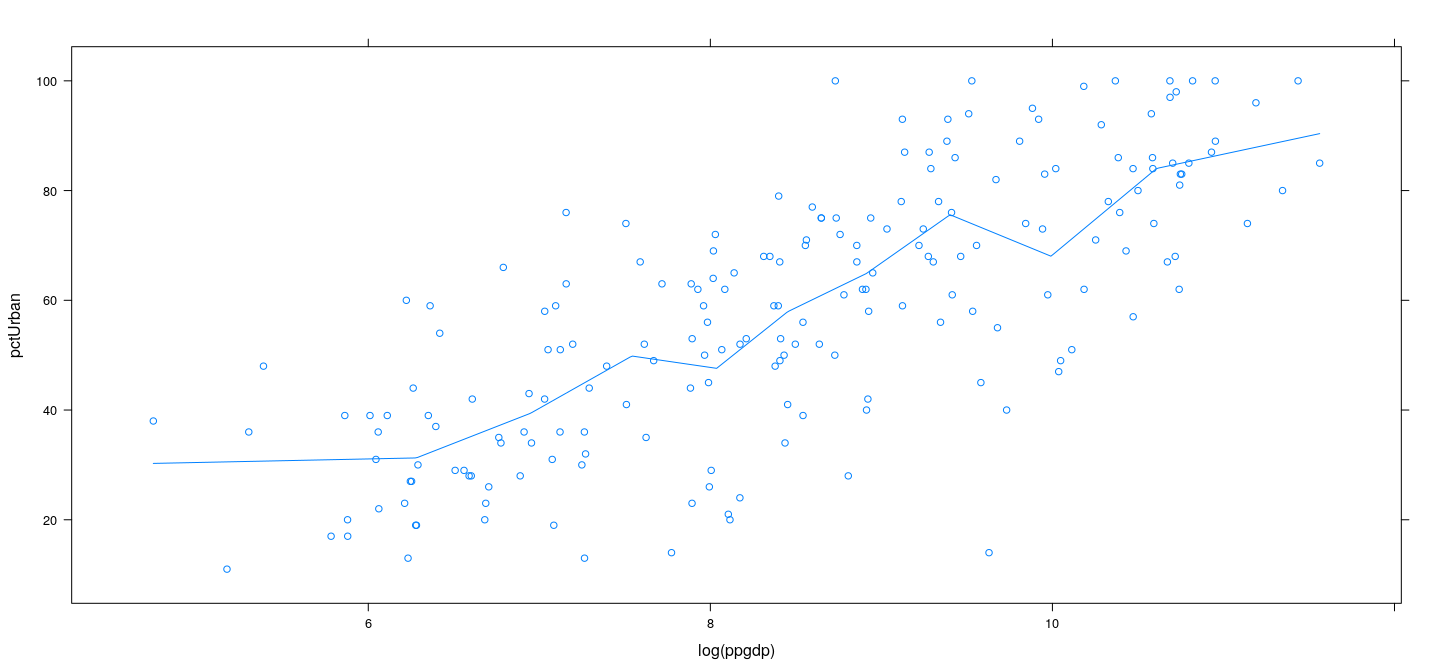
Natural generalization: piecewise quadratic interpolation
(with matching first derivatives)
\[ f(x) = \alpha_0 + \alpha_1 x + \beta_0 x^2 + \sum_{j=1}^{k-1} \beta_j (x-t_j)^2_{+} \]
where \(x_{+} = \max\{ 0, x \}\)
Natural generalization: piecewise quadratic interpolation
xyplot(pctUrban ~ log(ppgdp), data = UN) +
layer(panel.smoother(x, y, method = "lm", se = FALSE, n = 500, form = y ~ 1 + pquadint(x, knots = lgdp.knots)))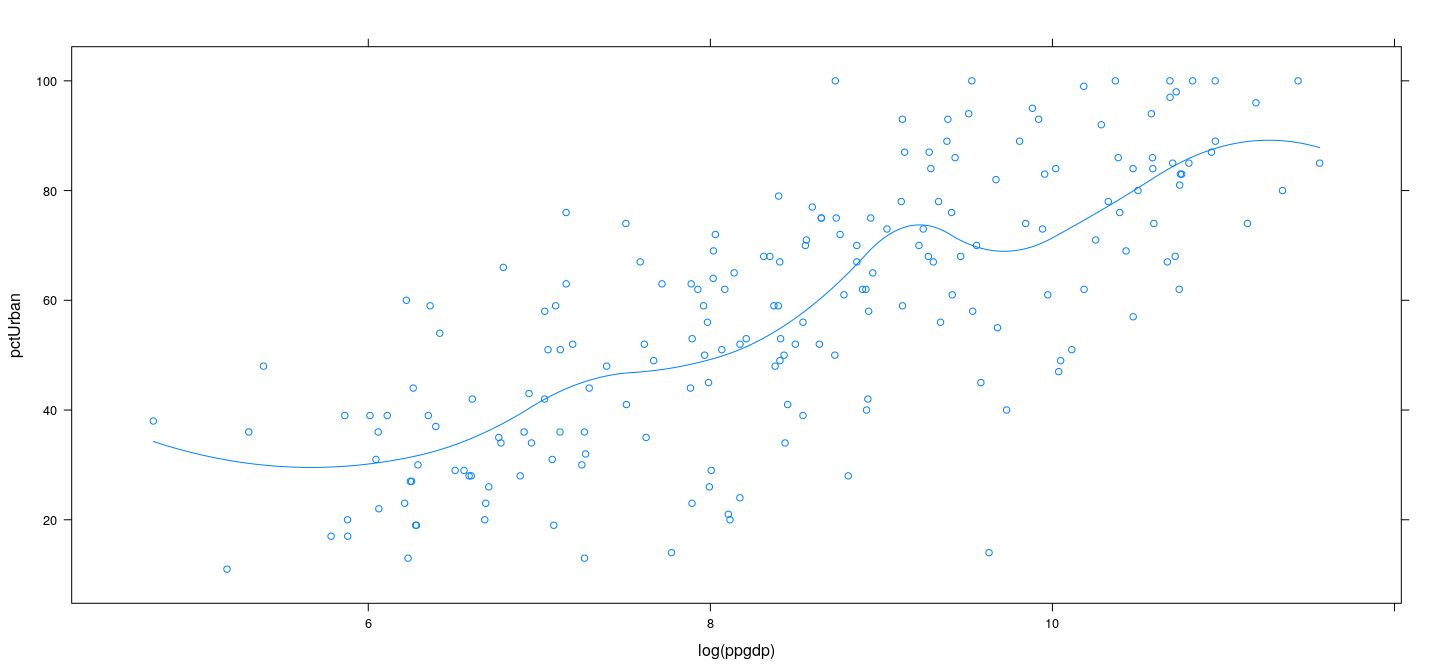
Further generalization: piecewise cubic interpolation
(with matching second derivatives)
\[ f(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \beta_0 x^3 + \sum_{j=1}^{k-1} \beta_j (x-t_j)^3_{+} \]
where \(x_{+} = \max\{ 0, x \}\)
Further generalization: piecewise cubic interpolation
xyplot(pctUrban ~ log(ppgdp), data = UN) +
layer(panel.smoother(x, y, method = "lm", se = FALSE,
form = y ~ 1 + pcubint(x, knots = lgdp.knots)))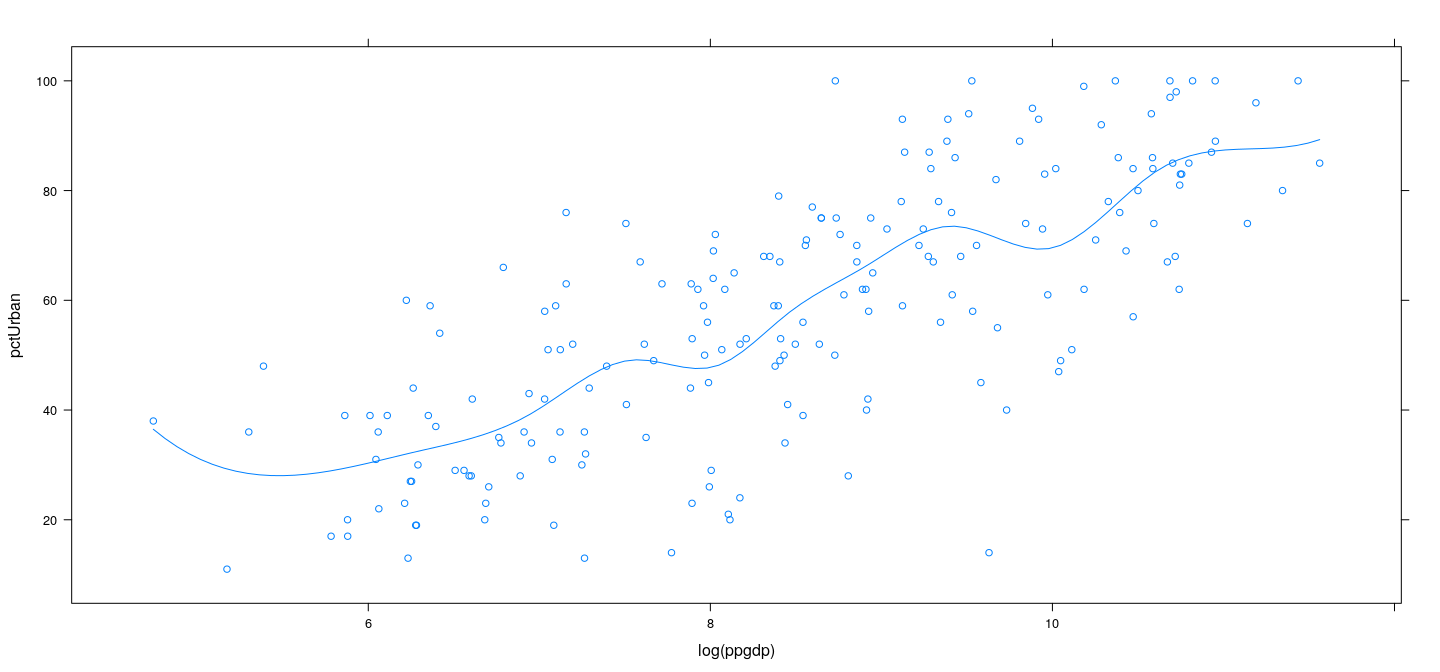
Also known as cubic spline regression
library(splines)
xyplot(pctUrban ~ log(ppgdp), data = UN) +
layer(panel.smoother(x, y, method = "lm", form = y ~ bs(x, knots = lgdp.knots[2:10]), se = FALSE))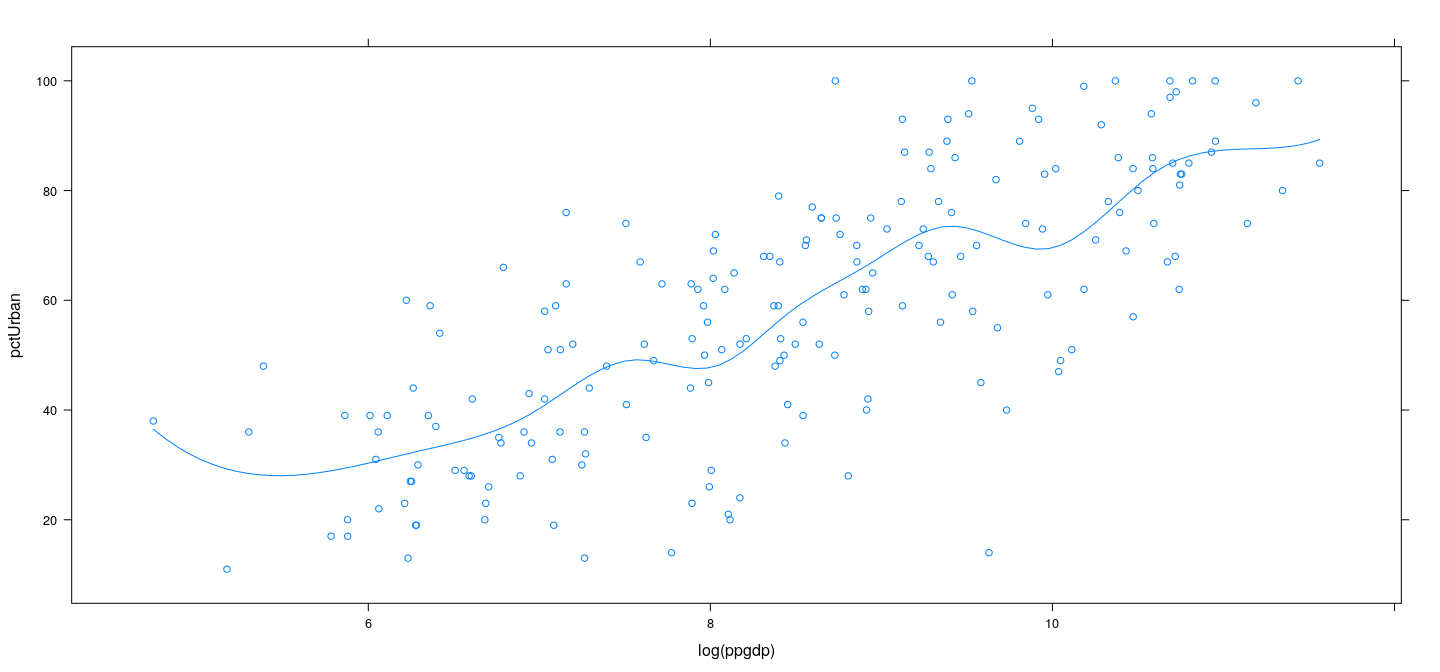
Regression with basis functions: background
Goal: Estimate best (least squares) \(\hat{f}\) within some class of functions
Example: “Interpolating splines” — piecewise cubic polynomials with continuous second derivatives
All the examples we have seen are vector spaces (for a fixed set of knots)
To find \(\hat{f}\) using a linear model, we need to find a basis
One example (for cubic interpolating splines) is \[ \{ 1, x, x^2, x^3 \} \cup \{ (x - t_j)^3_{+} : j = 1, ..., k-1 \} \]
Plot of cubic spline basis functions
u <- seq(0, 1, length = 101)
m <- as.data.frame(pcubint(u, knots = c(-Inf, c(0.25, 0.5, 0.75, Inf))))
names(m) <- paste0("f", seq_len(ncol(m)))
xyplot(f1 + f2 + f3 + f4 + f5 + f6 ~ u, data = cbind(u, m), type = "l", ylab = NULL, grid = TRUE)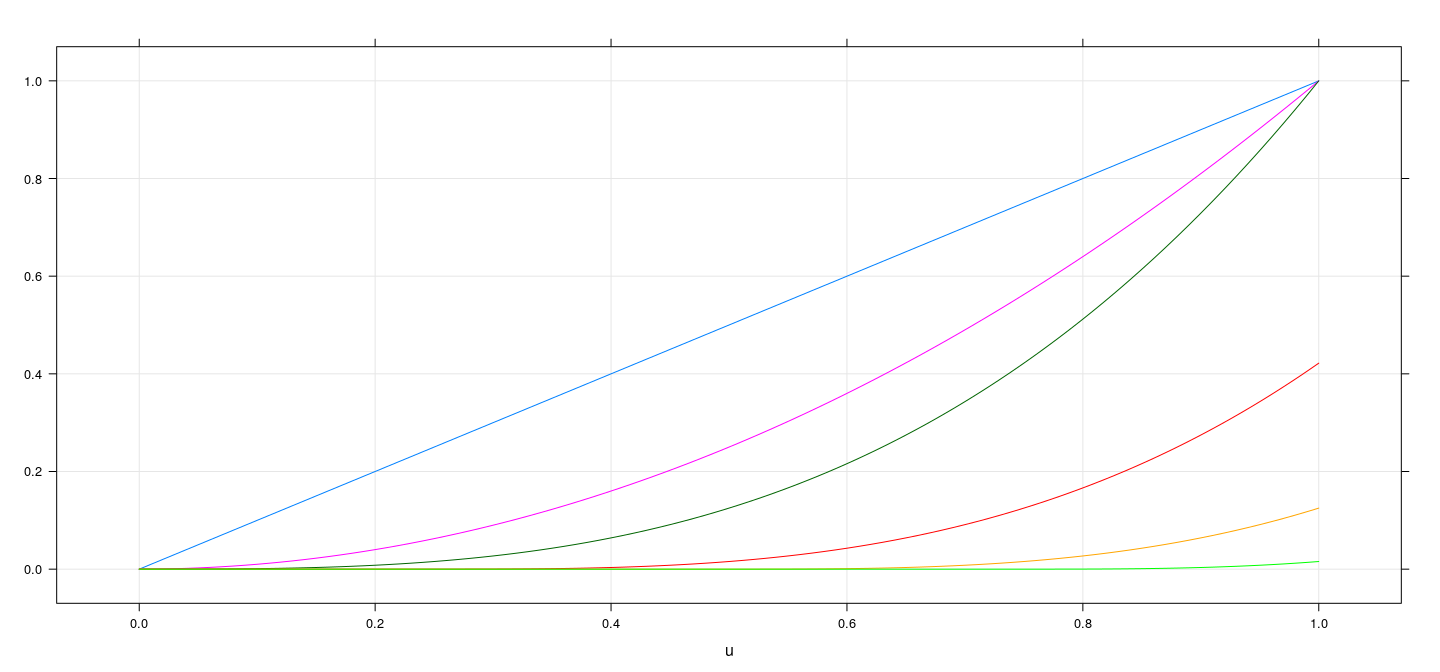
Alternative basis for cubic splines
u <- seq(0, 1, length = 101)
m <- as.data.frame(bs(u, knots = c(0.25, 0.5, 0.75)))
names(m) <- paste0("f", seq_len(ncol(m)))
xyplot(f1 + f2 + f3 + f4 + f5 + f6 ~ u, data = cbind(u, m), type = "l", ylab = NULL, grid = TRUE)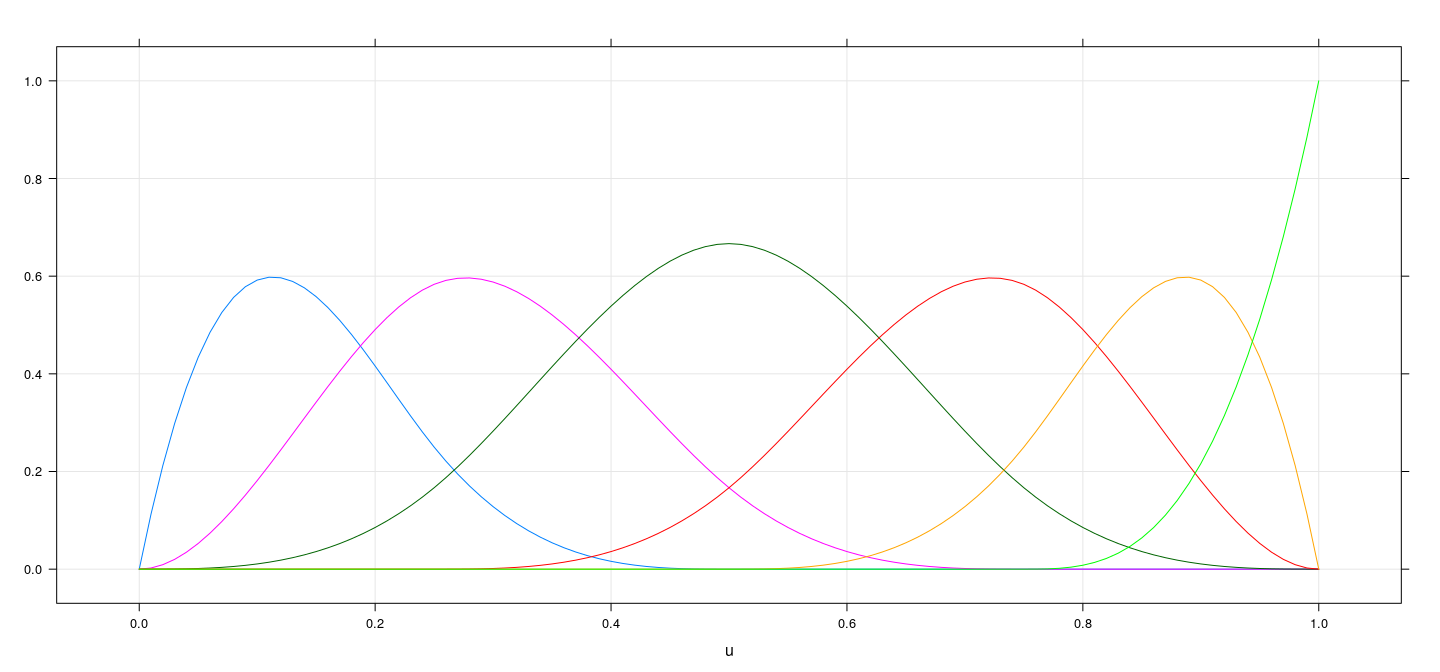
Basis splines in R
Available as the
bs()function in packagesplines(degree 3, “cubic”, by default)Usually specify
dfrather than explicit knots (tuning parameter providing flexibility)
Call:
lm(formula = pctUrban ~ 1 + bs(log(ppgdp), df = 6), data = UN)
Residuals:
Min 1Q Median 3Q Max
-58.942 -9.267 0.426 11.094 38.561
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 34.688 13.254 2.617 0.009573 **
bs(log(ppgdp), df = 6)1 -11.885 20.810 -0.571 0.568600
bs(log(ppgdp), df = 6)2 2.469 13.466 0.183 0.854691
bs(log(ppgdp), df = 6)3 21.769 14.884 1.463 0.145226
bs(log(ppgdp), df = 6)4 44.026 14.446 3.048 0.002631 **
bs(log(ppgdp), df = 6)5 46.601 16.149 2.886 0.004354 **
bs(log(ppgdp), df = 6)6 59.317 16.645 3.564 0.000462 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 15.65 on 192 degrees of freedom
(14 observations deleted due to missingness)
Multiple R-squared: 0.5674, Adjusted R-squared: 0.5539
F-statistic: 41.98 on 6 and 192 DF, p-value: < 2.2e-16Why splines?
Consider the problem of interpolation through \(k\) points
Obvious approach: Fit a polynomial
f <- function(x) 1 / (1 + x^2)
degree <- 4
x <- seq(-3, 3, length = degree + 1)
xyplot(f(x) ~ x, col = 1, pch = 16, ylim = c(-0.5, 1.1)) +
layer_(panel.curve(f, type = "l", col = "grey50")) +
layer(panel.smoother(x, y, method = "lm", form = y ~ poly(x, degree), se = FALSE))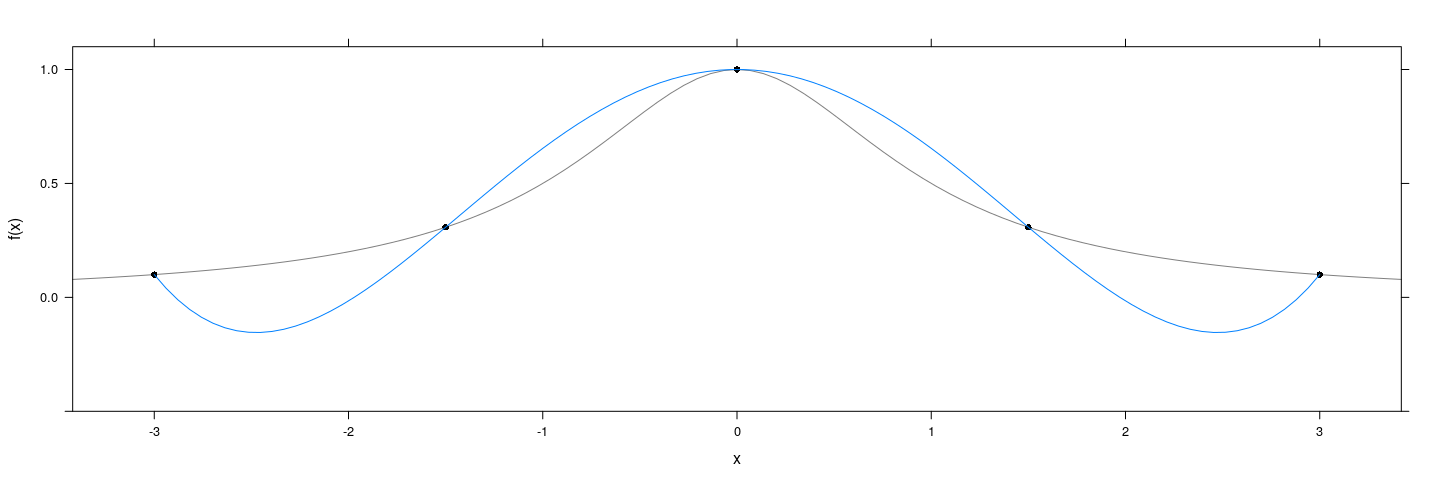
Why splines?
Consider the problem of interpolation through \(k\) points
Obvious approach: Fit a polynomial
f <- function(x) 1 / (1 + x^2)
degree <- 8
x <- seq(-3, 3, length = degree + 1)
xyplot(f(x) ~ x, col = 1, pch = 16, ylim = c(-0.5, 1.1)) +
layer_(panel.curve(f, type = "l", col = "grey50")) +
layer(panel.smoother(x, y, method = "lm", form = y ~ poly(x, degree), se = FALSE))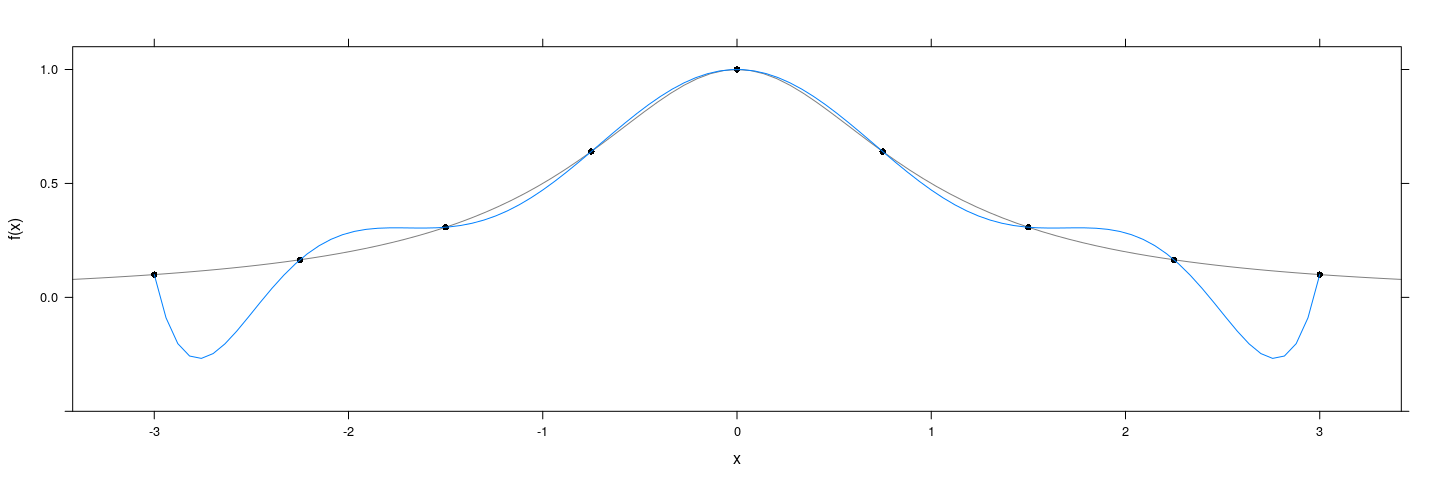
Why splines?
Consider the problem of interpolation through \(k\) points
Obvious approach: Fit a polynomial — Runge’s phenomenon
f <- function(x) 1 / (1 + x^2)
degree <- 12
x <- seq(-3, 3, length = degree + 1)
xyplot(f(x) ~ x, col = 1, pch = 16, ylim = c(-0.5, 1.1)) +
layer_(panel.curve(f, type = "l", col = "grey50")) +
layer(panel.smoother(x, y, method = "lm", form = y ~ poly(x, degree), se = FALSE))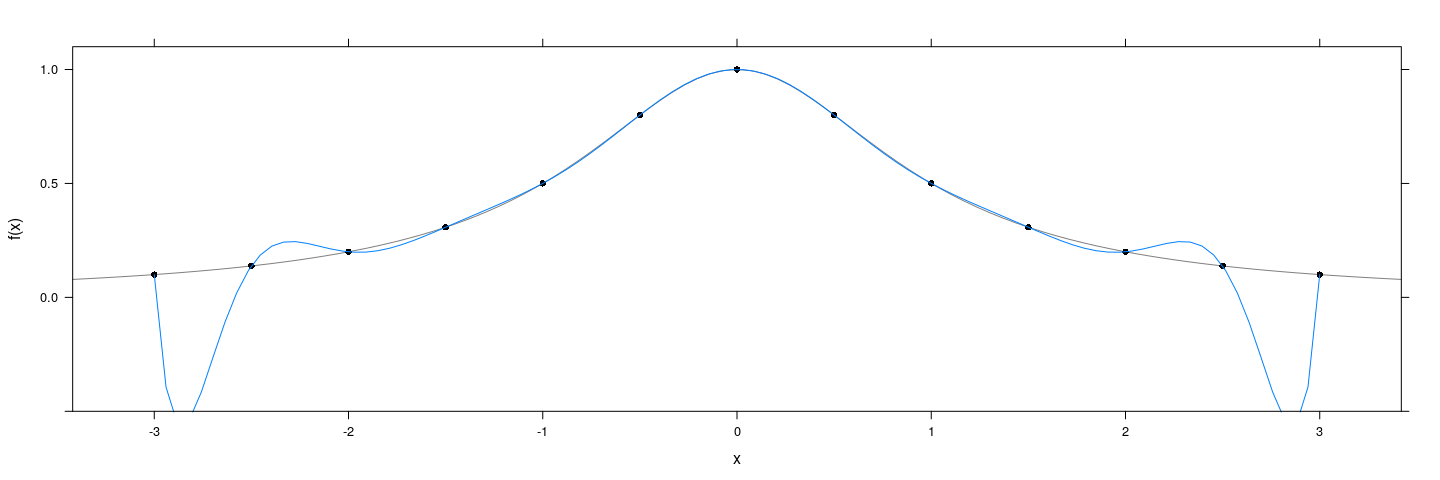
Why splines?
Consider the problem of interpolation through \(k\) points
Alternative: Fit a cubic spline
f <- function(x) 1 / (1 + x^2)
degree <- 12
x <- seq(-3, 3, length = degree + 1)
xyplot(f(x) ~ x, col = 1, pch = 16, ylim = c(-0.5, 1.1)) +
layer_(panel.curve(f, type = "l", col = "grey50")) +
layer(panel.lines(predict(interpSpline(x, y))))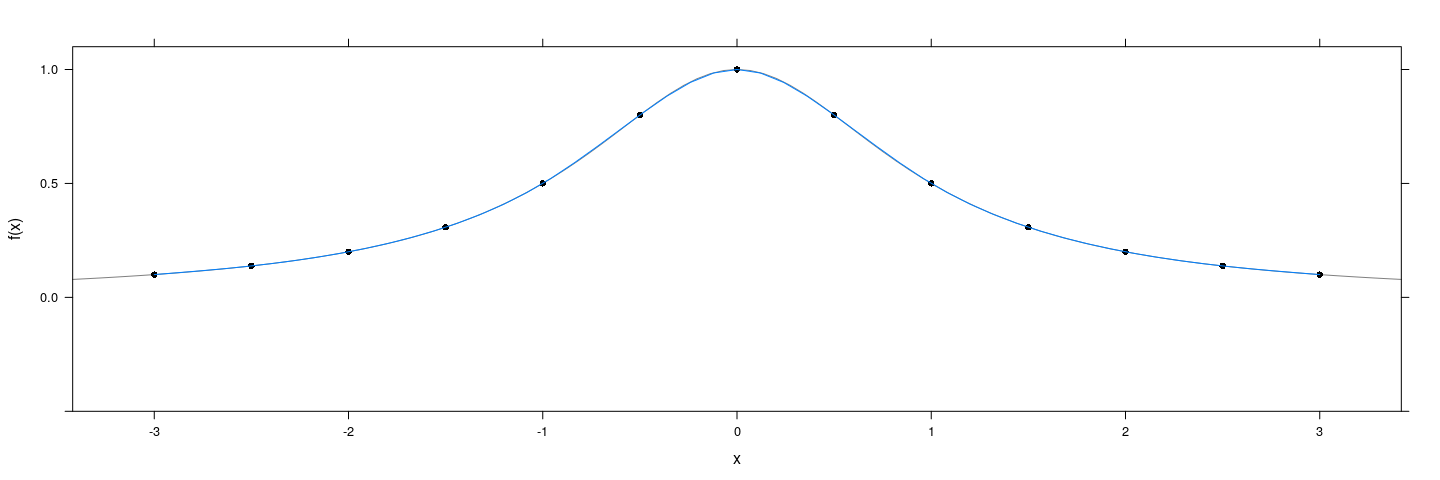
An interesting property of interpolating splines
Consider finding \(f: [a,b] \to \mathbb{R}\) interpolating the points \(\{ (x_i, y_i ) : x_i \in [a, b] \}\) that minimizes
\[ \int_{a}^{b} (f^{\prime\prime}(t))^2 dt \quad\quad \text{(roughness penalty)} \]
in the class of functions with continuous second derivative
- The solution is a “natural” cubic spline
- “Natural” because the solution is linear outside the range of the knots
Smoothing splines
A non-parametric regression approach motivated by this:
Find \(f\) to minimize (given \(\lambda > 0\))
\[ \sum_i (y_i - f(x_i))^2 + \lambda \int_{a}^{b} (f^{\prime\prime}(t))^2 dt \]
- The solution is a “natural” cubic spline
- \(\lambda\) represents a tuning parameter (smoothness vs flexibility)
- \(\lambda\) is usually chosen by a form of cross-validation
- The mathematical analysis of smoothing splines is relatively complicated (will not discuss)
Smoothing splines in R
UN.sub <- subset(UN, !is.na(ppgdp) & !is.na(pctUrban)) # cannot handle NA
fm.ss <- with(UN.sub, smooth.spline(log(ppgdp), pctUrban, df = 6)) # lambda controlled by df
fm.ssCall:
smooth.spline(x = log(ppgdp), y = pctUrban, df = 6)
Smoothing Parameter spar= 1.034826 lambda= 0.004116211 (12 iterations)
Equivalent Degrees of Freedom (Df): 6.000823
Penalized Criterion (RSS): 46566.24
GCV: 1031.185Call:
smooth.spline(x = log(ppgdp), y = pctUrban)
Smoothing Parameter spar= 1.499952 lambda= 9.443731 (25 iterations)
Equivalent Degrees of Freedom (Df): 2.030403
Penalized Criterion (RSS): 47818.1
GCV: 986.3203
Smoothing splines in R
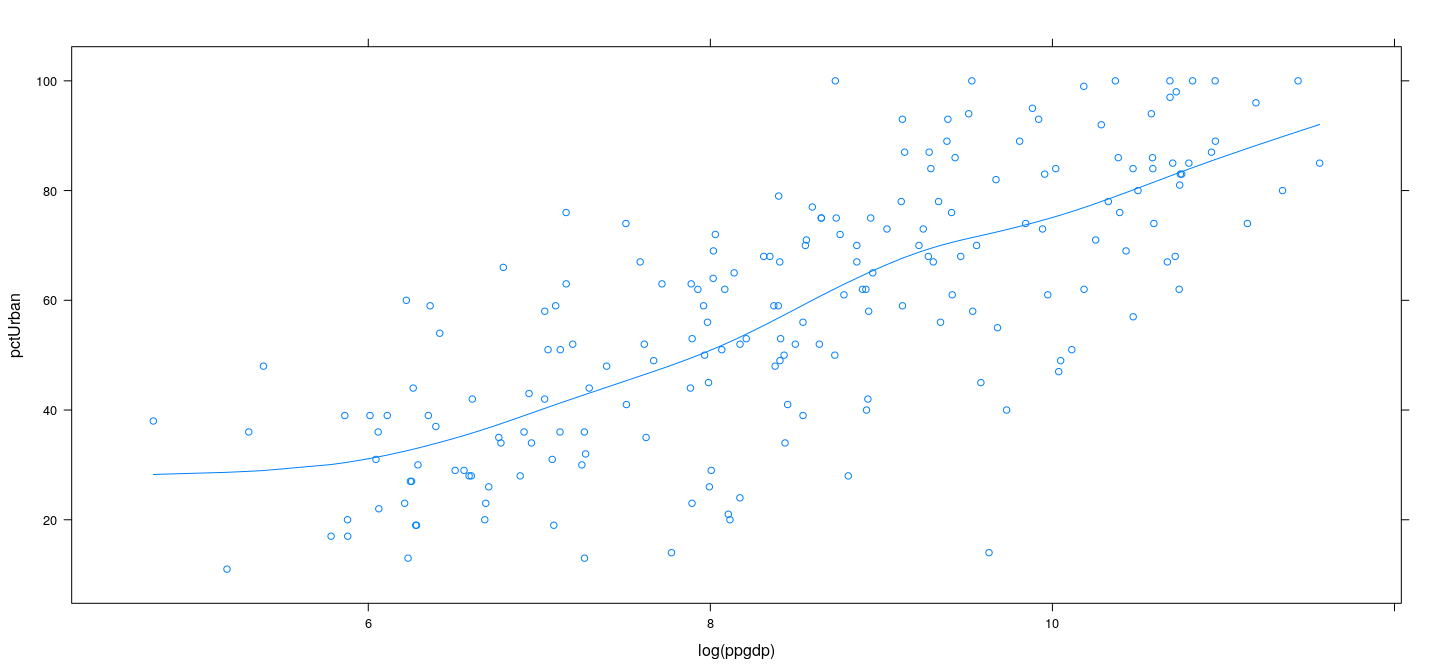
Smoothing splines in R
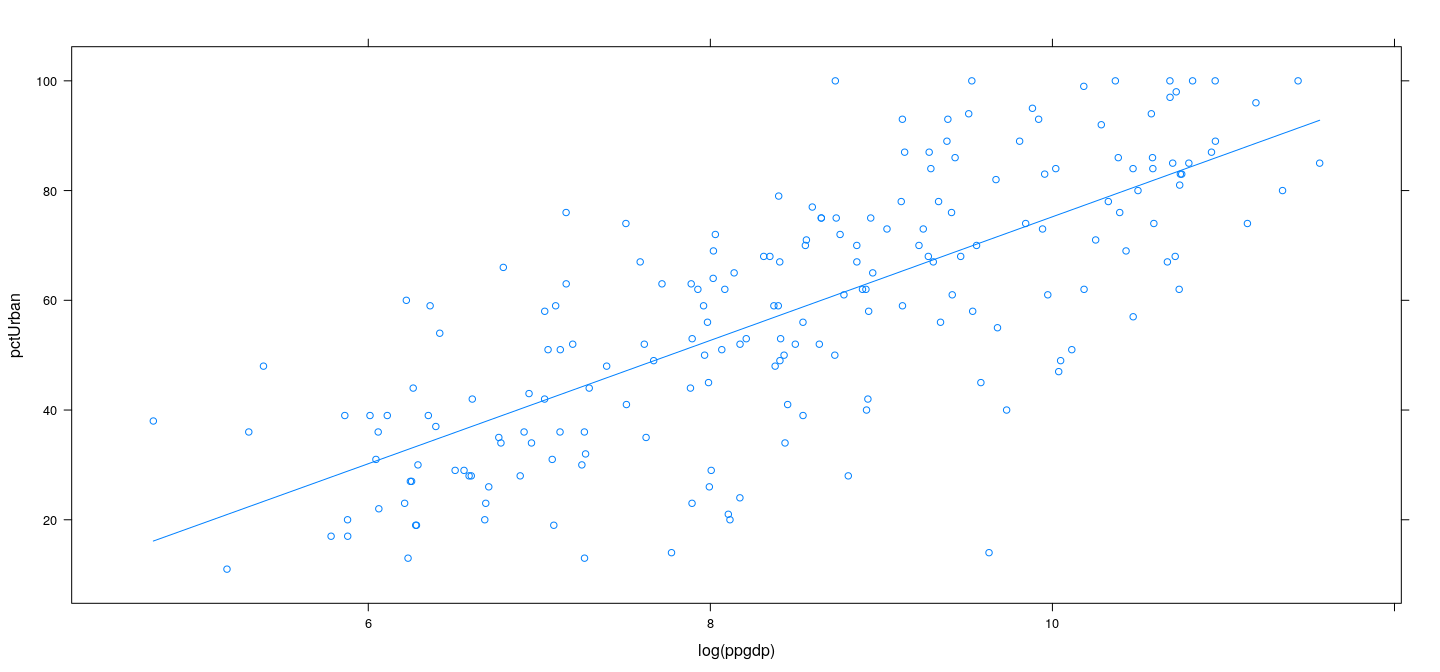
Summary: smooth regression for non-linear expectation function
Focuses on estimating \(f(x) = E(Y | X=x)\)
Several methods available, both non-parametric and parametric
Usually involves tuning parameter that needs to be chosen
Can be used to visually diagnose non-linearity of \(f(x)\)
What about non-constant variance?
Assume constant variance
Define \(\hat{\varepsilon}_i = y_i - \hat{f}(x_i)\)
Expect \(E( \lvert \hat{\varepsilon}_i \rvert) \propto \sigma\)
fm <- lm(pctUrban ~ log(ppgdp), data = UN)
xyplot(abs(residuals(fm)) ~ fitted(fm)) + layer(panel.smoother(x, y, method = "loess"))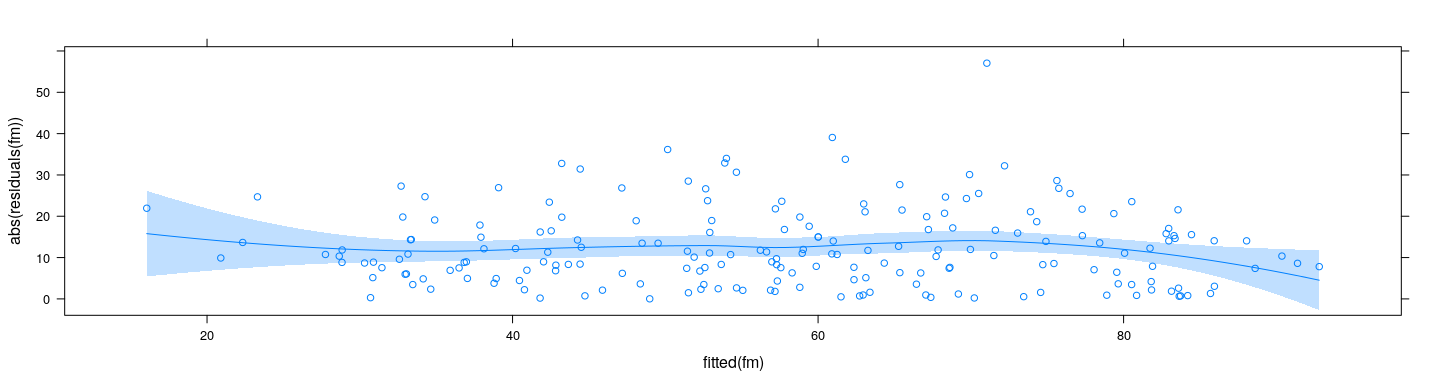
Summary: smooth regression for non-linear expectation function
Focuses on estimating \(f(x) = E(Y | X=x)\)
Several methods available, both non-parametric and parametric
Usually involves tuning parameter that needs to be chosen
Can be used to visually diagnose non-linearity of \(f(x)\)
Can also be used to diagnose heteroscedasticity