Robust Regression
Deepayan Sarkar
Motivation
Least squares regression is sensitive to violation of assumptions
Individual high-leverage points can substantially influence inference
Specifically, least squares is vulnerable when error distribution is heavy-tailed
We have considered one possible remedy: detect influential observations
This has several drawbacks:
- We cannot realistically expect users to always screen the data
- The binary decision to keep/reject suspicious observations seems extreme; we may instead prefer to downweight such observations
- Finding outliers may be difficult in multivariate or structured data
- Rejecting outliers changes the sampling distribution of estimates; we should but usually do not make adjustments.
- Another alternative is to consider procedures that systematically guard against outliers
Motivation: Location and scale
- A more familiar example before considering the regression problem:
\[ X_1, \dotsc, X_n \sim N(\mu, \sigma^2) \]
[1] 4.2967261 0.8741864 7.7031483 -0.0853126 2.5003953 5.6141429 8.6149780 11.0482167 -1.9215526 -0.3005308Want to estimate location \(\mu\) (as well as scale \(\sigma\))
Common estimators of location \(\mu\):
| Mean | mean(x) |
3.8344398 |
| Median | median(x) |
3.3985607 |
| Trimmed mean | mean(x, trim = 0.25) |
3.4838811 |
Robust estimation of location
How do these behave when data is “contaminated”?
We know that
- Mean can be changed by an arbitrary amount by changing a single observation
- Median can be changed arbitrarily only by changing more than 50% observations
- But there is a cost: median is less “efficient”!
Let us try to make these ideas formal
Relative efficiency
Consider two estimators \(T_1\) and \(T_2\)
Define the relative efficiency of \(T_1\) w.r.t. \(T_2\) (for a given underlying distribution) as
\[ RE(T_1; T_2) = \frac{V(T_2)}{V(T_1)} \]
For biased estimators, variance could be replaced by MSE
\(T_2\) is usually taken to be the optimal estimator, if one is available
What are relative efficiencies of median and trimmed mean?
Instead of trying to obtain variances theoretically (which is often difficult), we could use simulation to get a rough idea
Relative efficiency
sampling.variance <- function(estimator, rfun, n, NREP = 10000)
{
var(replicate(NREP, estimator(rfun(n))))
}
trim.mean <- function(x) mean(x, trim = 0.25)
rdist <- function(n) rnorm(n, mean = 5, sd = 3)
var.mean <- sampling.variance(mean, rdist, n = 10)
var.median <- sampling.variance(median, rdist, n = 10)
var.tmean <- sampling.variance(trim.mean, rdist, n = 10)
round(100 * var.mean / var.median)[1] 74[1] 91Asymptotic relative efficiency
\(ARE(T_1; T_2)\) is the limiting value of relative efficiency as \(n \to \infty\)
rdist <- function(n) rnorm(n, mean = 5, sd = 3)
var.mean <- sampling.variance(mean, rdist, n = 5000)
var.median <- sampling.variance(median, rdist, n = 5000)
var.tmean <- sampling.variance(trim.mean, rdist, n = 5000)
round(100 * var.mean / var.median)[1] 63[1] 84For comparison, the exact \(ARE\) of the median is \(\frac{2}{\pi} = 63.6\%\)
This is when the data comes from a normal distribution
Relative efficiency for heavier tails
- Suppose errors are instead from \(t\) with 5 degrees of freedom
rdist <- function(n) 5 + 3 * rt(n, df = 5)
var.mean <- sampling.variance(mean, rdist, n = 5000)
var.median <- sampling.variance(median, rdist, n = 5000)
var.tmean <- sampling.variance(trim.mean, rdist, n = 5000)
round(100 * var.mean / var.median)[1] 96[1] 121Winsorized trimmed mean
- Similar to trimmed mean, but replaces trimmed observations by nearest untrimmed observation
win.mean <- function(x, trim = 0.25)
{
q <- quantile(x, c(trim, 1-trim))
x[x < q[1]] <- q[1]
x[x > q[2]] <- q[2]
mean(x)
}
rdist <- function(n) rnorm(n, mean = 5, sd = 3) # normal
var.mean <- sampling.variance(mean, rdist, n = 5000)
var.win.mean <- sampling.variance(win.mean, rdist, n = 5000)
round(100 * var.mean / var.win.mean)[1] 91rdist <- function(n) 5 + 3 * rt(n, df = 5) # t_5
var.mean <- sampling.variance(mean, rdist, n = 5000)
var.win.mean <- sampling.variance(win.mean, rdist, n = 5000)
round(100 * var.mean / var.win.mean)[1] 117Relative efficiency for contamination
Another “departure” model: contamination
Suppose data is a mixture of \(N(\mu, \sigma^2)\) with probability \(1-\epsilon\) and \(N(\mu, 9\sigma^2)\) with probability \(\epsilon\)
rdist <- function(n) rnorm(n, mean = 5, sd = ifelse(runif(n) < 0.01, 3, 1)) # 1% contamination
var.mean <- sampling.variance(mean, rdist, n = 5000)
var.median <- sampling.variance(median, rdist, n = 5000)
var.tmean <- sampling.variance(trim.mean, rdist, n = 5000)
round(100 * var.mean / c(median = var.median, trim.mean = var.tmean)) median trim.mean
69 92 rdist <- function(n) rnorm(n, mean = 5, sd = ifelse(runif(n) < 0.05, 3, 1)) # 5% contamination
var.mean <- sampling.variance(mean, rdist, n = 5000)
var.median <- sampling.variance(median, rdist, n = 5000)
var.tmean <- sampling.variance(trim.mean, rdist, n = 5000)
round(100 * var.mean / c(median = var.median, trim.mean = var.tmean)) median trim.mean
82 108 Sensitivity / influence function
How much does changing one observation change the estimate \(T\)?
This is measured by the empirical influence function or sensitivity curve
\[ SC(x; x_1, \dotsc, x_{n-1}, T) = \frac{ T(x_1, \dotsc, x_{n-1}, x) - T(x_1, \dotsc, x_{n-1}) }{ 1/n } \]
We are usually interested in limiting behaviour as \(n \to \infty\)
The population version, independent of the sample \(x_1, \dotsc, x_{n-1}\), is known as the influence function
\[ IF(x; F, T) = \lim_{\epsilon \to 0} \frac{ T( (1-\epsilon) F + \epsilon \delta_x) - T(F) }{\epsilon} \]
- Here \(\delta_x\) is a point mass at \(x\)
Sensitivity / influence function
How does
mean(c(x, xnew))change as function ofxnew?How do other estimates change?
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.28099 -0.61800 -0.06070 -0.06727 0.51522 2.01596 xx <- seq(-5, 5, 0.01)
sensitivity <-
data.frame(xx = xx,
mean = n * (sapply(xx, function(xnew) mean(c(x, xnew))) - mean(x)),
median = n * (sapply(xx, function(xnew) median(c(x, xnew))) - median(x)),
tmean = n * (sapply(xx, function(xnew) trim.mean(c(x, xnew))) - trim.mean(x)),
wmean = n * (sapply(xx, function(xnew) win.mean(c(x, xnew))) - win.mean(x)))Sensitivity / influence function
xyplot(mean + median + tmean + wmean ~ xx, sensitivity, type = "l", outer = TRUE,
xlab = "Additional observation", ylab = "Sensitivity", grid = TRUE) +
layer(panel.rug(x = .GlobalEnv$x))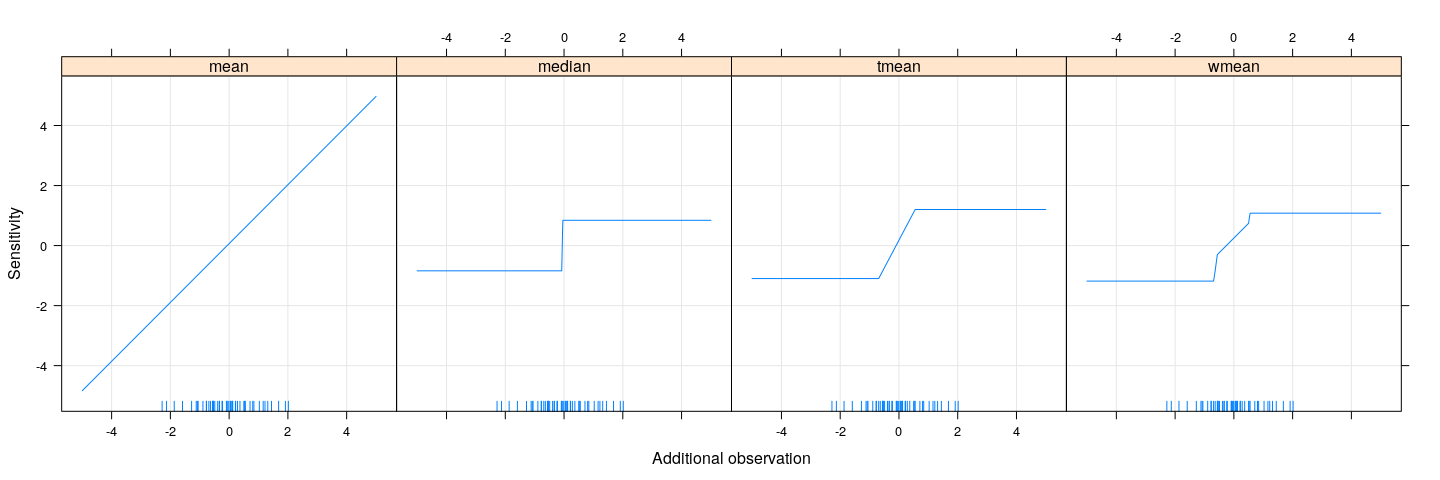
Breakdown point
Defined as the proportion of the sample size that must be perturbed to make the estimate unbounded
50% is the best we can hope for
For location, mean has 0% breakdown point (one out of \(n\)), median has 50%.
Estimators of scale
We can similarly consider estimators of scale \(\sigma\)
Common estimators:
- Sample standard deviation (
sdin R) - Mean absolute deviation from mean
- Median absolute deviation (MAD) from median (
madin R) - Inter-quartile range (
IQRin R)
- Sample standard deviation (
May need scaling for normal distribution:
Relative efficiency for estimators of scale
rdist <- function(n) rnorm(n, mean = 5) # Normal
var.T1 <- sampling.variance(T1, rdist, n = 5000)
var.T2 <- sampling.variance(T2, rdist, n = 5000)
var.T3 <- sampling.variance(T3, rdist, n = 5000)
var.T4 <- sampling.variance(T4, rdist, n = 5000)
round(100 * var.T1 / c(mean.abs.dev = var.T2, median.abs.dev = var.T3, iqr = var.T4)) mean.abs.dev median.abs.dev iqr
89 38 38 rdist <- function(n) rnorm(n, mean = 5, sd = ifelse(runif(n) < 0.01, 3, 1)) # 1% Contamination
var.T1 <- sampling.variance(T1, rdist, n = 5000)
var.T2 <- sampling.variance(T2, rdist, n = 5000)
var.T3 <- sampling.variance(T3, rdist, n = 5000)
var.T4 <- sampling.variance(T4, rdist, n = 5000)
round(100 * var.T1 / c(mean.abs.dev = var.T2, median.abs.dev = var.T3, iqr = var.T4)) mean.abs.dev median.abs.dev iqr
152 70 70 M-estimators
- Most common location estimators can be expressed as M-estimators (MLE-like)
\[ T(x_1, \dotsc, x_n) = \arg \min_{\theta} \sum_{i=1}^n \rho(x_i, \theta) \]
For MLE, \(\rho(x_i, \theta)\) is the negative log-density, but \(\rho\) need not correspond to a likelihood
If \(\psi(x_i, \theta) = \frac{d}{d\theta} \rho(x_i, \theta)\) exists, then \(T\) is the solution to the score equation
\[ \sum_{i=1}^n \psi(x_i, \theta) = 0 \]
We usually consider loss functions of the form \(\rho(x - \theta)\)
Corresponding \(\psi\) function is \(\psi(x - \theta) = \rho^{\prime}(x - \theta)\) (disregarding change in sign)
This easily generalizes to vector parameters
M-estimators
- Mean
\[ \rho(x - \theta) = (x-\theta)^2, \quad \psi(x - \theta) = 2 (x-\theta) \]
- Median (ignoring non-differentiability of \(\lvert x \rvert\) at 0)
\[ \rho(x - \theta) = \lvert x-\theta \rvert, \quad \psi(x - \theta) = \text{sign}(x-\theta) \]
- Trimmed mean (for some \(c\), ignoring dependence of \(c\) on the data)
\[ \rho(x - \theta) = \begin{cases} (x-\theta)^2 & \lvert x - \theta \rvert \leq c \\ c^2 & \text{otherwise} \end{cases} \]
\[ \psi(x - \theta) = \begin{cases} 2 (x-\theta) & \lvert x - \theta \rvert \leq c \\ 0 & \text{otherwise} \end{cases} \]
M-estimators
- Huber loss (similar to Winsorized trimmed mean)
\[ \rho(x - \theta) = \begin{cases} (x-\theta)^2 & \lvert x - \theta \rvert \leq c \\ c (2 \lvert x-\theta \rvert - c) & \text{otherwise} \end{cases} \]
\[ \psi(x - \theta) = \begin{cases} -2c & x - \theta < -c \\ 2 (x-\theta) & \lvert x - \theta \rvert \leq c \\ 2c & x - \theta > c \end{cases} \]
Can be thought of compromise between mean (squared error) and median (absolute error)
Estimator reduces to mean as \(c \to \infty\), median as \(c \to 0\)
\(\rho\) is differentiable everywhere
- Exercise: What do plots of \(\rho\) and \(\psi\) look like?
Influence function revisited
xx <- seq(-3, 3, 0.01)
sensitivity <-
data.frame(xx = xx,
mean = 2 * xx,
median = sign(xx),
tmean = ifelse(abs(xx) < 1, 2 * xx, 0),
huber = ifelse(abs(xx) < 1, 2 * xx, 2 * sign(xx)))
xyplot(mean + median + tmean + huber ~ xx, sensitivity, type = "l", outer = TRUE,
xlab = "x", ylab = expression(psi(x)), grid = TRUE)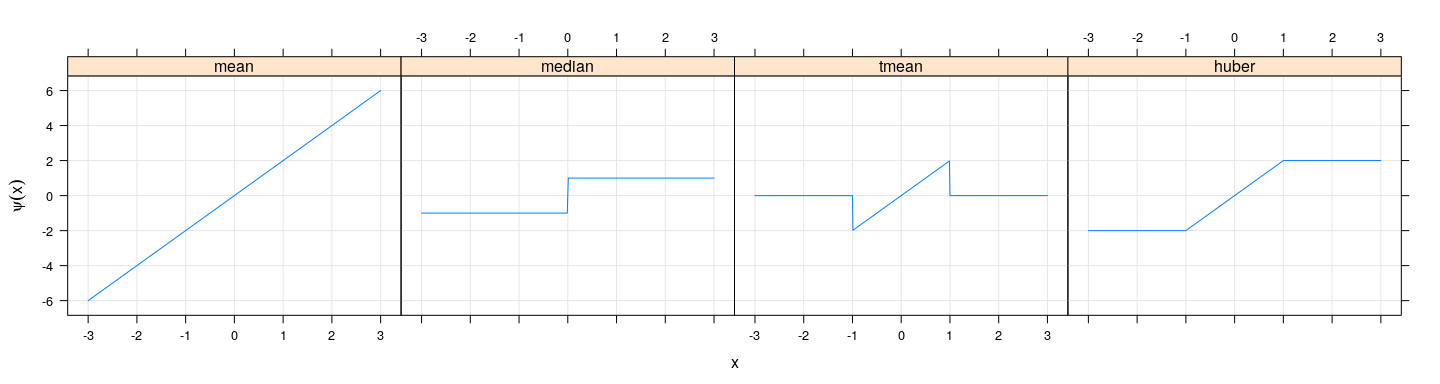
- Turns out that the corresponding influence functions have the same shape (but will not discuss why)
M-estimation: general approach for location
Choose function \(\psi(x - \theta)\)
Find \(T\) by solving (for \(\theta\))
\[ \sum_{i=1}^n \psi(x_i - \theta) = 0 \]
- We can rewrite this as
\[ \sum_{i=1}^n \frac{\psi(x_i - \theta)}{(x_i - \theta)} (x_i - \theta) = 0 \]
M-estimation: general approach for location
This suggests an iterative approach using weighted least squares in each step:
- Start with initial estimate \(\hat\theta\)
- Obtain current weights \(w_i = \frac{\psi(x_i - \hat\theta)}{(x_i - \hat\theta)}\)
- Obtain new estimate of \(\theta\) by solving \(\sum_i w_i (x_i - \theta) = 0 \implies \hat\theta = \sum_i w_i x_i / \sum_i w_i\)
Of course, a black-box numerical optimizer (e.g.,
optim()) can also be used instead
Common robust loss function derivatives
Absolute deviation \(\psi(x) = \text{sign}(x)\)
Huber (same as Winsorized trimmed mean)
\[ \psi(x) = \begin{cases} -c & x < c \\ x & \lvert x \rvert \leq c \\ c & x > c \end{cases} \]
- Trimmed mean
\[ \psi(x) = \begin{cases} x & \lvert x \rvert \leq c \\ 0 & \text{otherwise} \end{cases} \]
- Tukey bisquare
\[ \psi(x) = x \left[ 1 - (x/R)^2 \right]_{+}^2 \quad \text{ for } \rho(x) = \begin{cases} R^2 \left[ 1 - (1 - (x/R)^2) \right]^3 & \lvert x \rvert \leq R \\ R^2 & \text{otherwise} \end{cases} \]
- For the last three, choice of scale (\(c\), \(R\)) is a tuning parameter
Common robust loss function derivatives
xx <- seq(-2, 2, 0.01)
c <- 1; R <- 1
psi <-
data.frame(xx = xx,
median = sign(xx),
huber = ifelse(abs(xx) <= c, xx, c * sign(xx)),
tmean = ifelse(abs(xx) <= c, xx, 0),
bisquare = xx * pmax(0, (1 - (xx/R)^2))^2)
xyplot(median + huber + tmean + bisquare ~ xx, psi, type = "l", outer = TRUE,
ylab = expression(psi(x)), xlab = "x", grid = TRUE)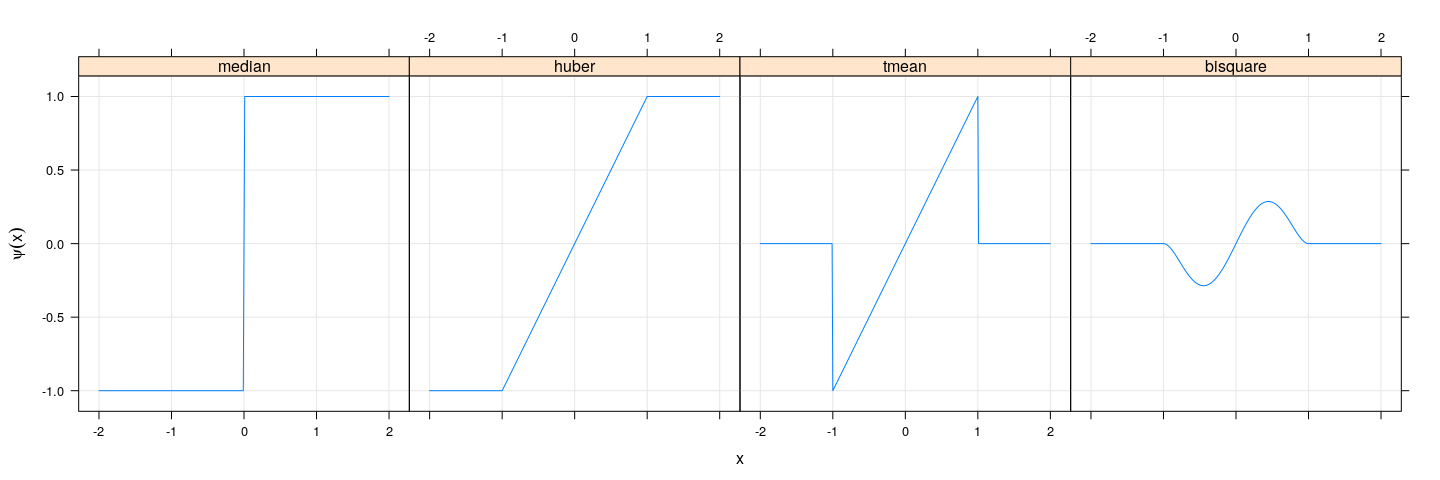
Common robust loss function derivatives
The last two functions are examples of “redescending” influence functions
Corresponding loss function \(\rho\) becomes flat beyond a threshold
In effect, beyond this threshold, extreme observations are completely discounted
In other words, they have zero/constant contribution to the total loss
However, this does make the objective function (to be minimized) non-convex
- Let us see what the objective function looks like for various loss functions
huber.loss <- function(x, c = 1) ifelse(abs(x) < c, x^2, c * (2 * abs(x) - c))
bisquare.loss <- function(x, R = 1) ifelse(abs(x) < R, R^2 * (1 - (1 - (x/R)^2))^3, R^2)
x <- rnorm(10)
y <- c(x, 10.1, 10.2, 10.3) # add three extreme observations to x
t <- seq(-5, 15, 0.01)
Example: loss functions
SSE <- sapply(t, function(theta) sum((x - theta)^2))
SAD <- sapply(t, function(theta) sum(abs(x - theta)))
SH <- sapply(t, function(theta) sum(huber.loss(x - theta, c = 1)))
SBS <- sapply(t, function(theta) sum(bisquare.loss(x - theta, R = 1)))
xyplot(SSE + SAD + SH + SBS ~ t, type = "l", outer = TRUE,
ylab = "Loss", xlab = "theta", grid = TRUE, scales = list(y = "free")) +
layer(panel.rug(x = .GlobalEnv$x))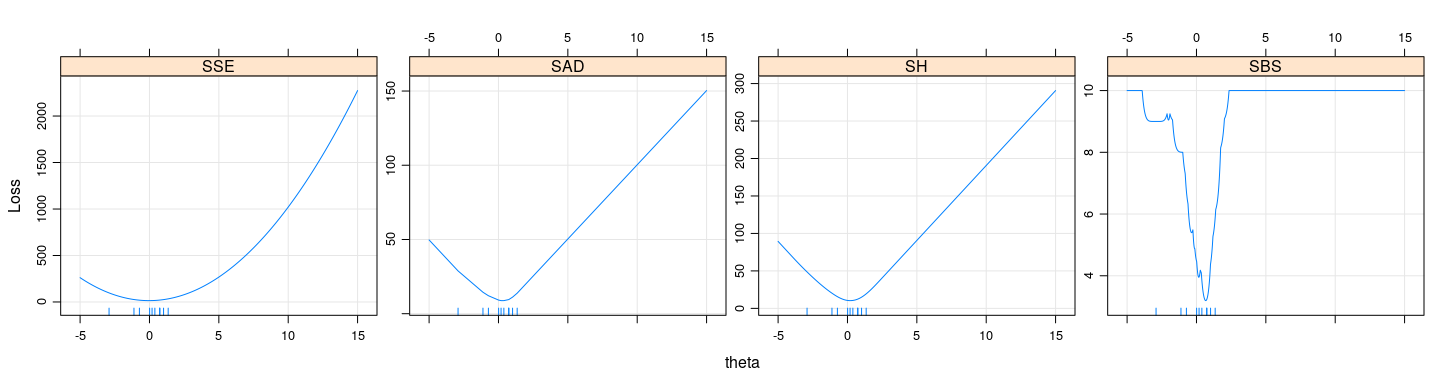
Example: loss functions
SSE <- sapply(t, function(theta) sum((y - theta)^2))
SAD <- sapply(t, function(theta) sum(abs(y - theta)))
SH <- sapply(t, function(theta) sum(huber.loss(y - theta, c = 1)))
SBS <- sapply(t, function(theta) sum(bisquare.loss(y - theta, R = 1)))
xyplot(SSE + SAD + SH + SBS ~ t, type = "l", outer = TRUE,
ylab = "Loss", xlab = "theta", grid = TRUE, scales = list(y = "free")) +
layer(panel.rug(x = .GlobalEnv$y))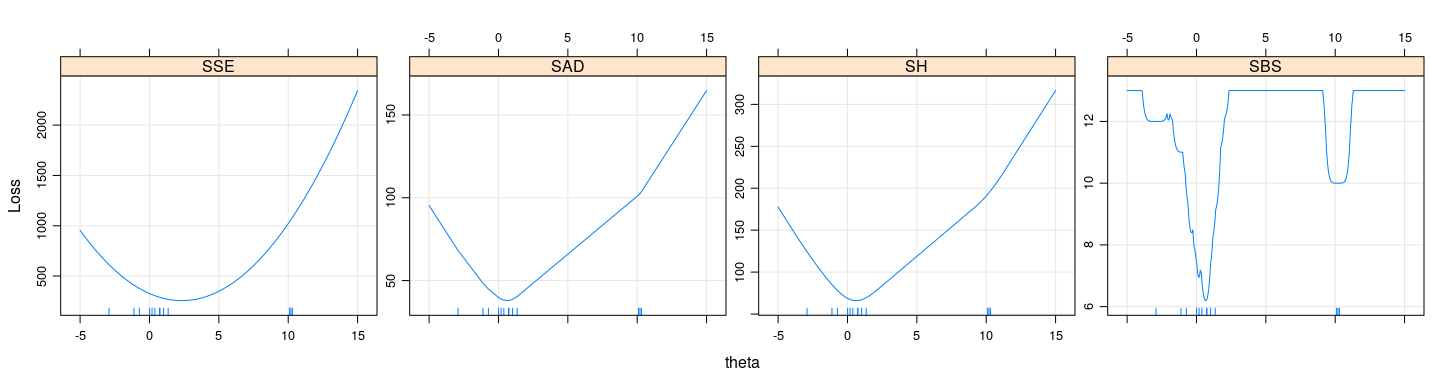
- For non-convex loss functions, important to have good starting estimates
Other practical considerations
Tuning parameters are arbitrary
Natural to express tuning parameter in terms of scale \(\sigma\) (unknown) — scale invariance
Common to take \(\hat\sigma\) to be a multiple of the median absolute deviation (MAD) from the median
Tuning parameter can then be chosen to achieve some target asymptotic relative efficiency under normality
For example, Huber loss function with \(c = 1.345 \sigma\) would give 95% \(ARE\) if \(\sigma\) was known
Standard errors
- M-estimators are consistent and asymptotically normal with variance \(\tau \sigma^2 / n\), where
\[ \tau = \frac{E(\psi^2(X))}{ [ E(\psi^{\prime}(X)) ]^2 } \]
- Could be estimated by replacing \(X\) by fitted (standardized) residuals
\[ \hat\tau = \frac{\frac{1}{n} \sum_i \psi^2(e_i / \hat\sigma)}{ [ \frac{1}{n} \sum_i \psi^{\prime}(e_i / \hat\sigma) ]^2 } \]
- Not necessarily reliable in small samples
M-estimation for regression
The ideas described above translate directly to linear regression
Instead of minimizing least squared errors, minimize
\[ \sum_{i=1}^n \rho(y_i - \mathbf{x}_i^T \beta) \]
- Simple estimation approach: Iteratively (Re)Weighted Least Squares (IWLS / IRLS) with weights
\[ w_i^{(t+1)} = \frac{\psi\left(y_i - \mathbf{x}_i^T \hat{\beta}^{(t)}\right)} {y_i - \mathbf{x}_i^T \hat{\beta}^{(t)}} = \frac{\psi(e_i^{(t)})}{e_i^{(t)}} > 0 \]
Implemented in the
rlm()function (in theMASSpackage) among othersBy default, scale is estimated using MAD of residuals (updated for each iteration)
M-estimation example: Bisquare
library(MASS)
fm <- rlm(weight ~ height, data = Davis, psi = psi.bisquare)
xyplot(weight ~ height, Davis, type = c("p", "r"), grid = TRUE) + layer(panel.abline(fm, col = "red"))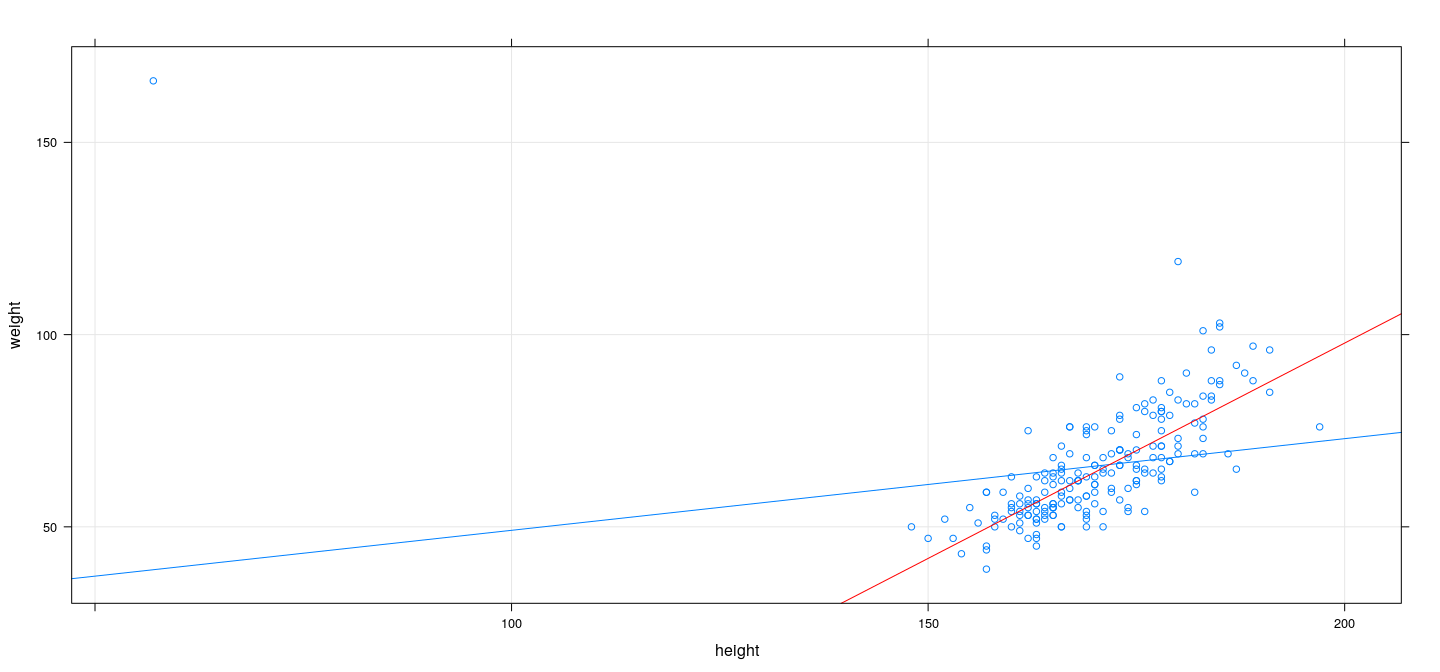
M-estimation example: Huber
library(MASS)
fm <- rlm(weight ~ height, data = Davis, psi = psi.huber)
xyplot(weight ~ height, Davis, type = c("p", "r"), grid = TRUE) + layer(panel.abline(fm, col = "red"))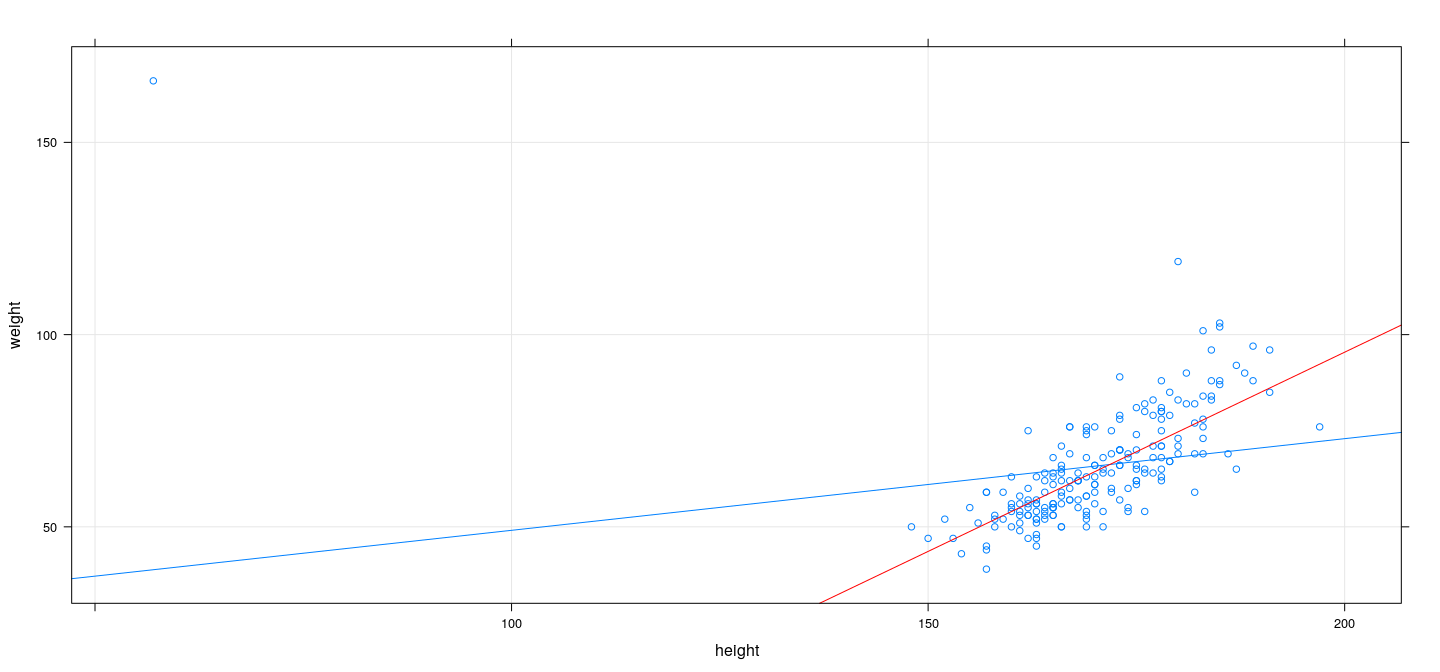
M-estimation example: Least absolute deviation (using optim())
L <- function(p) with(Davis, sum(abs(weight - p[1] - p[2] * height)))
bhat <- optim(coef(fm), L)$par
xyplot(weight ~ height, Davis, type = c("p", "r"), grid = TRUE) + layer(panel.abline(bhat, col = "red"))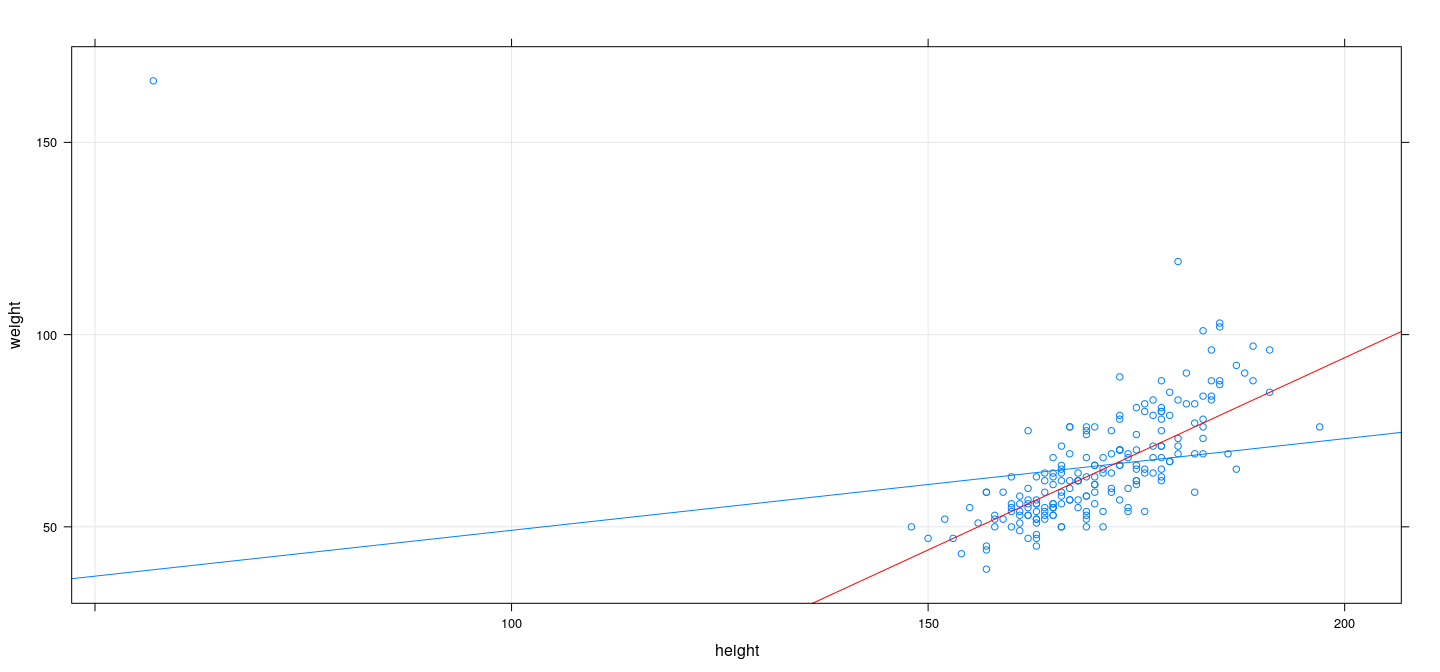
M-estimation example: multiple regression
fm1 <- lm(prestige ~ income + education, data = Duncan, na.action = na.exclude)
fm2 <- rlm(prestige ~ income + education, data = Duncan, psi = psi.bisquare, na.action = na.exclude)
fm3 <- rlm(prestige ~ income + education, data = Duncan, psi = psi.huber, na.action = na.exclude)
coefficients(summary(fm1)) Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.0646629 4.27194117 -1.419650 1.630896e-01
income 0.5987328 0.11966735 5.003310 1.053184e-05
education 0.5458339 0.09825264 5.555412 1.727192e-06 Value Std. Error t value
(Intercept) -7.4121192 3.87702087 -1.911808
income 0.7902166 0.10860468 7.276082
education 0.4185775 0.08916966 4.694169 Value Std. Error t value
(Intercept) -7.1107028 3.88131509 -1.832034
income 0.7014493 0.10872497 6.451593
education 0.4854390 0.08926842 5.437970M-estimation example: weights as diagnostics
- IWLS weights give an alternative measure of influence
wts <- fm2$w # bisquare
id <- which(wts < 0.6)
xyplot(wts ~ seq_along(wts)) +
layer(panel.text(x[id], y[id], labels = rownames(Duncan)[id], pos = 4, col = "grey50"))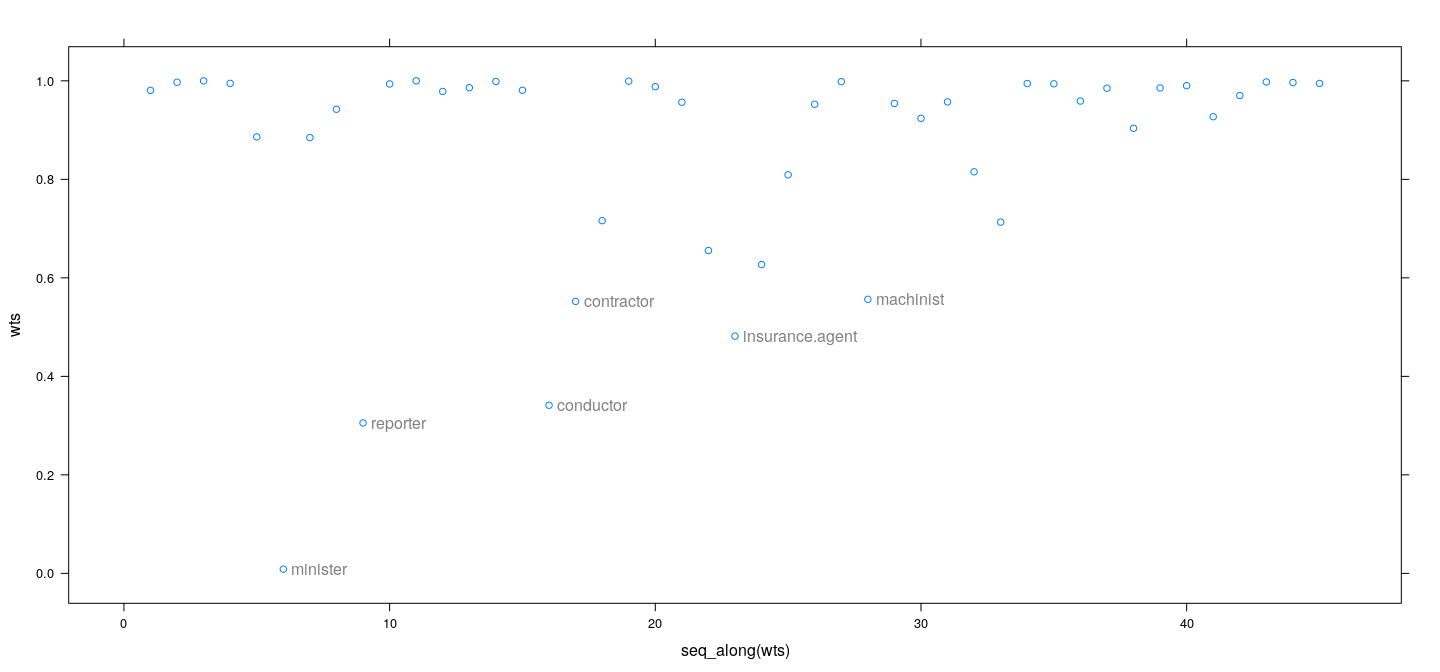
M-estimation example: weights as diagnostics
- IWLS weights give an alternative measure of influence
wts <- fm3$w # Huber
id <- which(wts < 0.6)
xyplot(wts ~ seq_along(wts)) +
layer(panel.text(x[id], y[id], labels = rownames(Duncan)[id], pos = 4, col = "grey50"))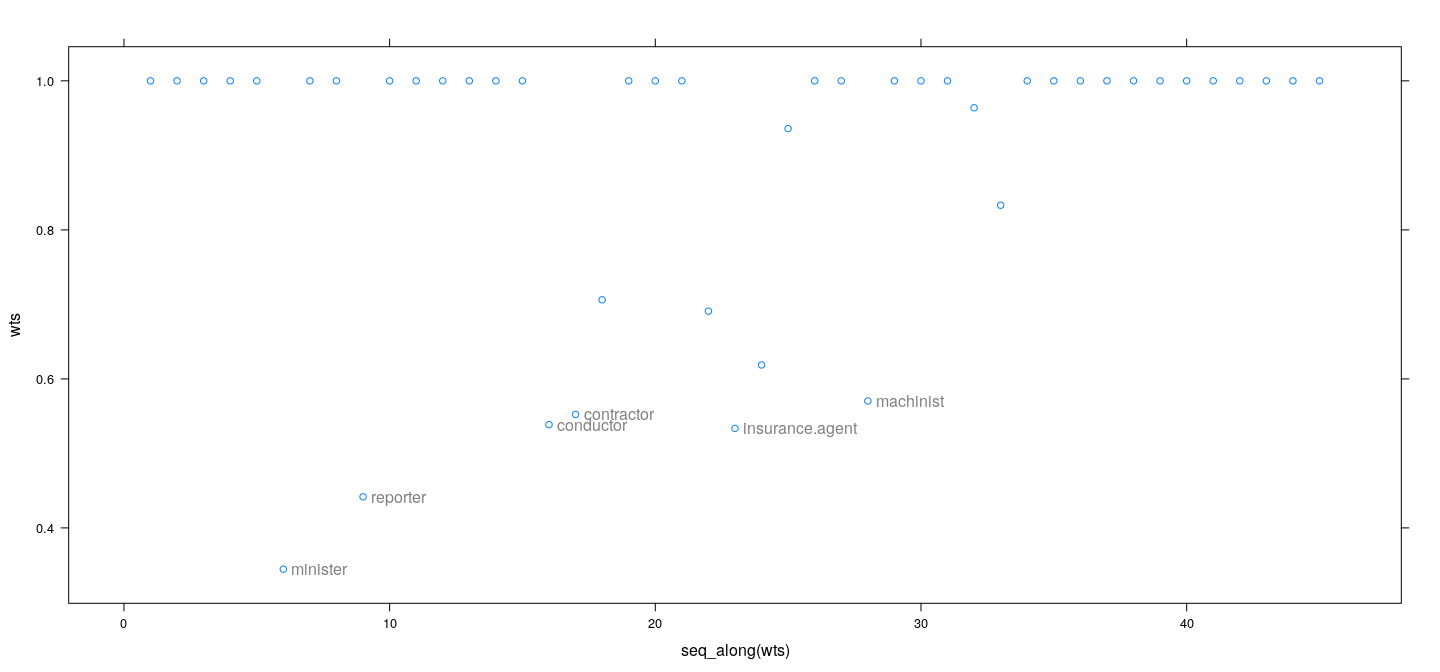
Does M-estimation ensure high breakdown point?
Example: Number of phone calls (in millions) in Belgium
Data available in the
MASSpackageFor 1964–1969, length of calls (in minutes) had been recorded instead of number
Does M-estimation ensure high breakdown point?
data(phones, package = "MASS")
fm2 <- rlm(calls ~ year, data = phones, psi = psi.huber, maxit = 100)
fm3 <- rlm(calls ~ year, data = phones, psi = psi.bisquare)
xyplot(calls ~ year, data = phones, grid = TRUE, type = c("p", "r"), pch = 16) +
layer(panel.abline(fm2, col = "red")) + layer(panel.abline(fm3, col = "black"))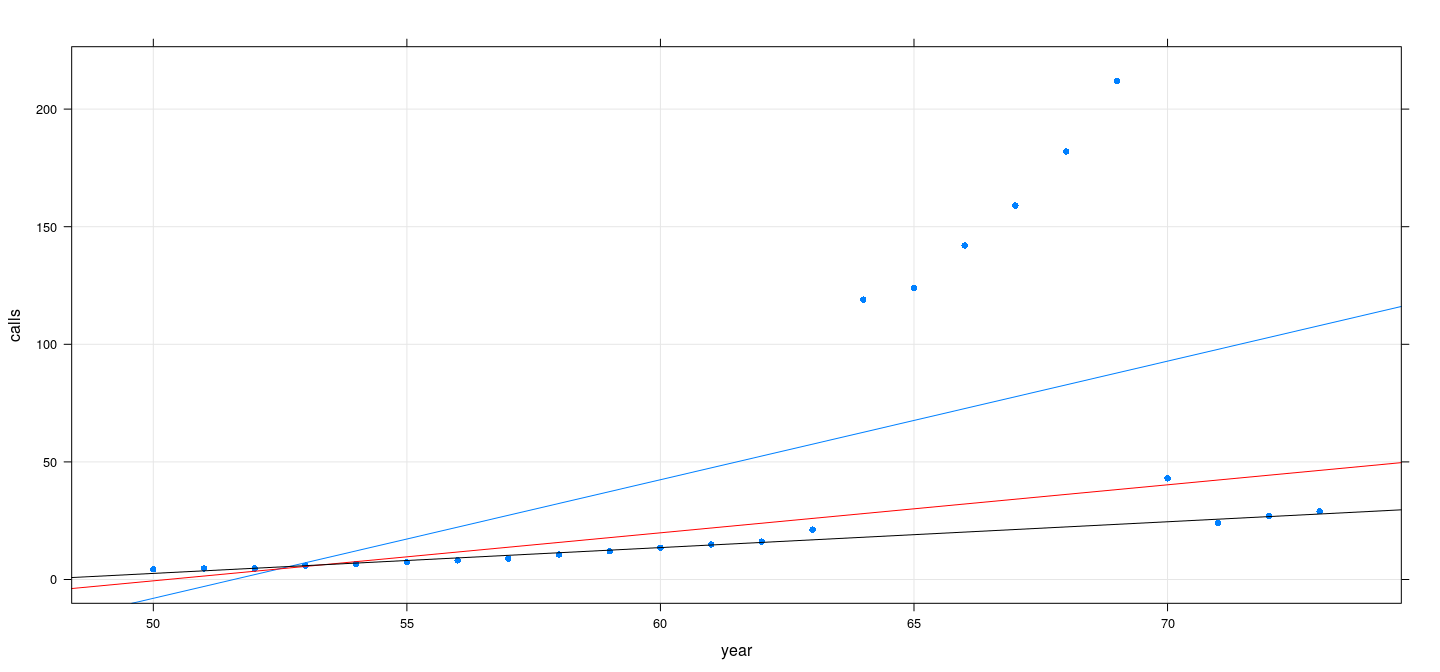
An artificial example
x <- c(1:10, 18)
y <- c(1:10, 18 + 10)
fm.h <- rlm(y ~ x, psi = psi.huber, maxit = 100)
fm.bs <- rlm(y ~ x, psi = psi.bisquare)
xyplot(y ~ x, pch = 16) + layer(panel.abline(fm.h, col = "red")) + layer(panel.abline(fm.bs, col = "black"))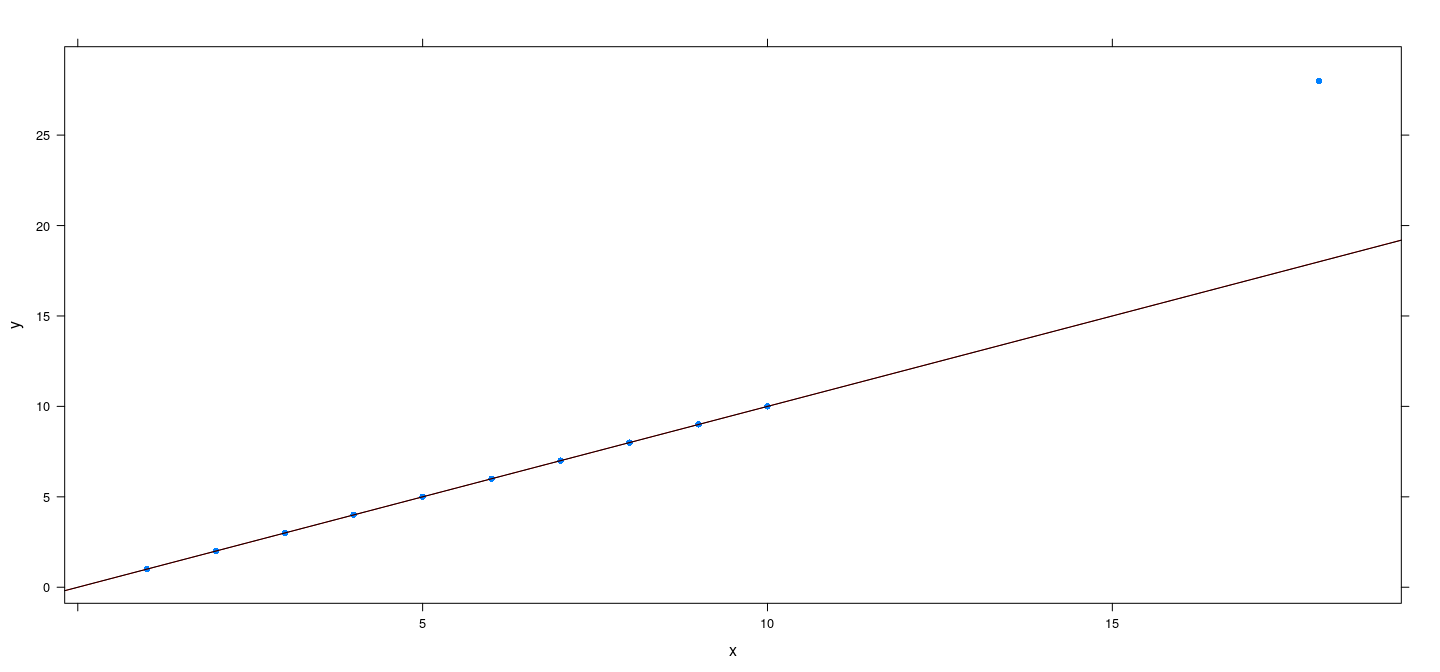
An artificial example
x <- c(1:10, 19)
y <- c(1:10, 19 + 10)
fm.h <- rlm(y ~ x, psi = psi.huber, maxit = 200)
fm.bs <- rlm(y ~ x, psi = psi.bisquare, maxit = 200)
xyplot(y ~ x, pch = 16) + layer(panel.abline(fm.h, col = "red")) + layer(panel.abline(fm.bs, col = "black"))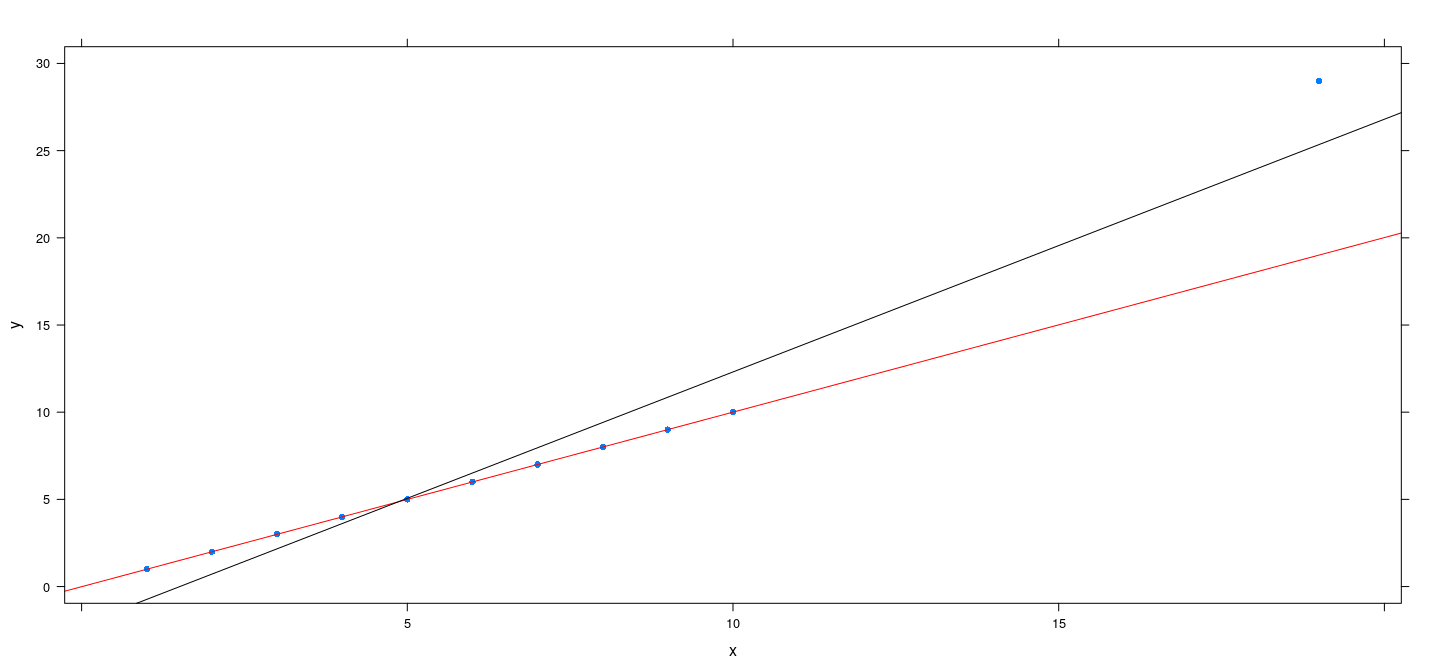
An artificial example
x <- c(1:10, 20)
y <- c(1:10, 20 + 10)
fm.h <- rlm(y ~ x, psi = psi.huber, maxit = 100)
fm.bs <- rlm(y ~ x, psi = psi.bisquare)
xyplot(y ~ x, pch = 16) + layer(panel.abline(fm.h, col = "red")) + layer(panel.abline(fm.bs, col = "black"))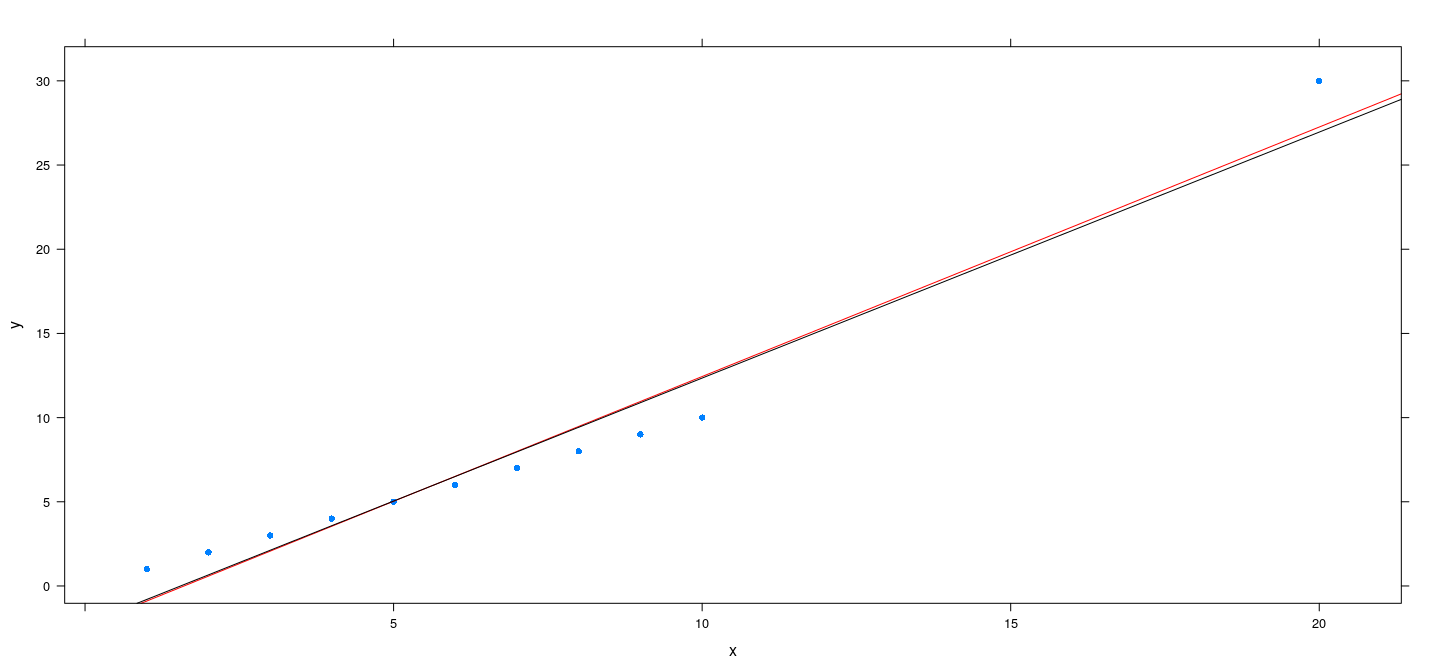
Why does this happen?
M-estimation approach can ensure high breakdown point for univariate location estimation
This is not automatically true for regression
Increasing loss function (LAD, Huber): sufficiently high-leverage outlier can always attract optimum line
Loss functions that flatten out (Bisquare): result depends on choice of \(c\) (which is estimated)
In general, no guarantee that M-estimation approach has bounded influence in regression
Resistant regression
Resistant alternatives exist, but are much more difficult to fit computationally
We will mention two examples: LMS and LTS regression
Least Median of Squares (LMS) regression: Find \(\hat{\beta}\) as
\[ \arg \min_\beta \mathrm{median}\left\lbrace (y_i - \mathbf{x}_i^T \beta)^2 ; i = 1, \dotsc, n\right\rbrace \]
More generally, LQS minimizes some quantile of the squared errors
Least Trimmed Squares (LTS) regression: Find \(\hat{\beta}\) as
\[ \arg \min_\beta \sum_{i=1}^q (y_i - \mathbf{x}_i^T \beta)^2_{(i)} \]
Here the objective is the sum of the \(q\) smallest error terms
The recommended value of \(q\) is \(\lfloor (n + p + 1) / 2 \rfloor\)
Resistant regression: LMS and LTS
Both LMS/LQS and LTS have high resistance (breakdown point) but low efficiency
LMS/LQS has lower efficiency than LTS, and there is no reason to prefer LMS over LTS
Computation of both are difficult
The
MASSpackage provides one implementation inlmsreg()andltsreg()
Example: Number of phone calls (in millions) in Belgium
data(phones, package = "MASS")
fm2 <- lmsreg(calls ~ year, data = phones)
fm3 <- ltsreg(calls ~ year, data = phones)
xyplot(calls ~ year, data = phones, grid = TRUE, type = c("p", "r"), pch = 16) +
layer(panel.abline(fm2, col = "red")) + layer(panel.abline(fm3, col = "black"))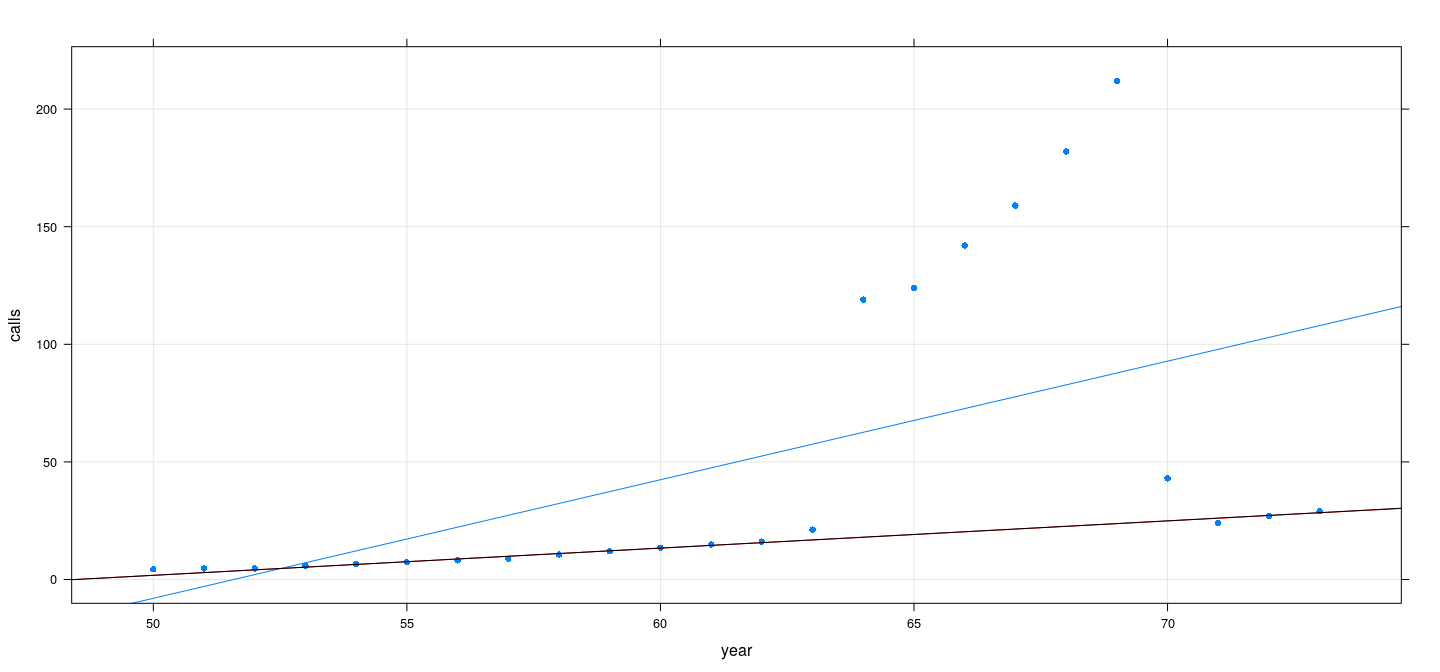
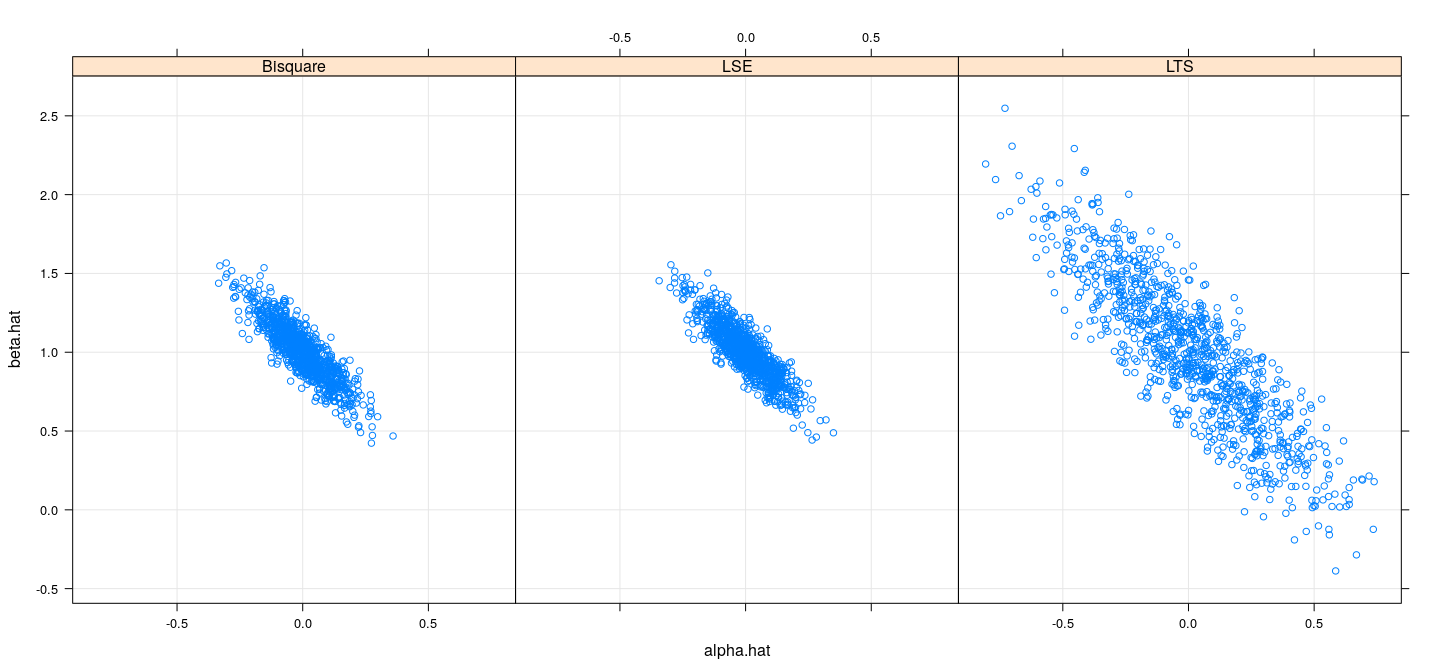
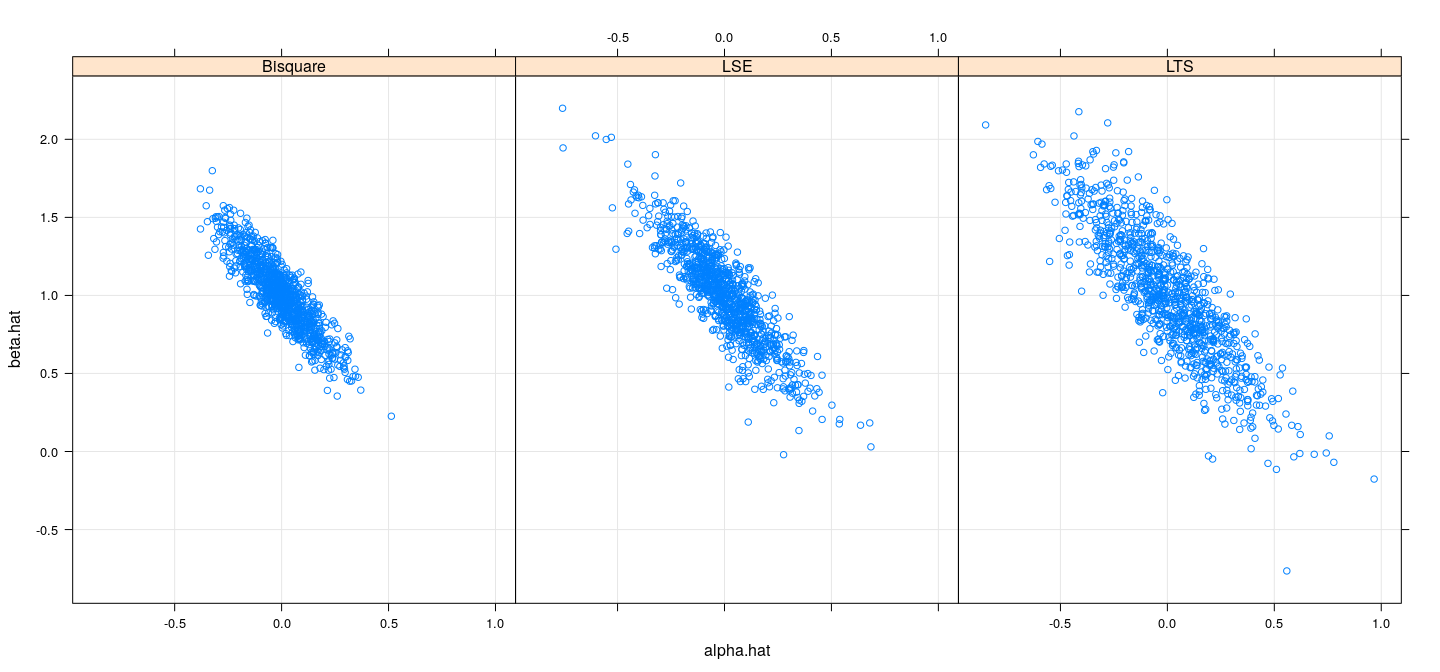
Efficiency comparison: simulation study (normal)
simulateCoefN <- function(n)
{
x <- runif(n, 0, 1)
y <- x + 0.5 * rnorm(n)
fm1 <- lm(y ~ x)
fm2 <- rlm(y ~ x, psi = psi.bisquare)
fm3 <- ltsreg(y ~ x)
data.frame(rbind(coef(fm1), coef(fm2), coef(fm3)),
model = c("LSE", "Bisquare", "LTS"))
}
sim.coefsn <- replicate(1000, simulateCoefN(100), simplify = FALSE)
sim.coefsn.df <- do.call(rbind, sim.coefsn)
names(sim.coefsn.df) <- c("alpha.hat", "beta.hat", "model")Efficiency comparison: simulation study (normal)
Efficiency comparison: simulation study (\(t_3\))
simulateCoefT <- function(n)
{
x <- runif(n, 0, 1)
y <- x + 0.5 * rt(n, df = 3)
fm1 <- lm(y ~ x)
fm2 <- rlm(y ~ x, psi = psi.bisquare)
fm3 <- ltsreg(y ~ x)
data.frame(rbind(coef(fm1), coef(fm2), coef(fm3)),
model = c("LSE", "Bisquare", "LTS"))
}
sim.coefst <- replicate(1000, simulateCoefT(100), simplify = FALSE)
sim.coefst.df <- do.call(rbind, sim.coefst)
names(sim.coefst.df) <- c("alpha.hat", "beta.hat", "model")Efficiency comparison: simulation study (\(t_3\))
MM-estimation
M-estimation with Bisquare error has reasonable efficiency
Should have high breakdown point if scale is “correctly” estimated
High breakdown potentially fails if initial scale estimate is too high
MM-estimation tries to ensure high breakdown point with high efficiency of Bisquare loss
First step is to obtain a better scale estimate using S-estimation (will not discuss)
This is followed by M-estimation with Bisquare loss function calibrated by estimated scale
Implemented in
rlm()withmethod = "MM"
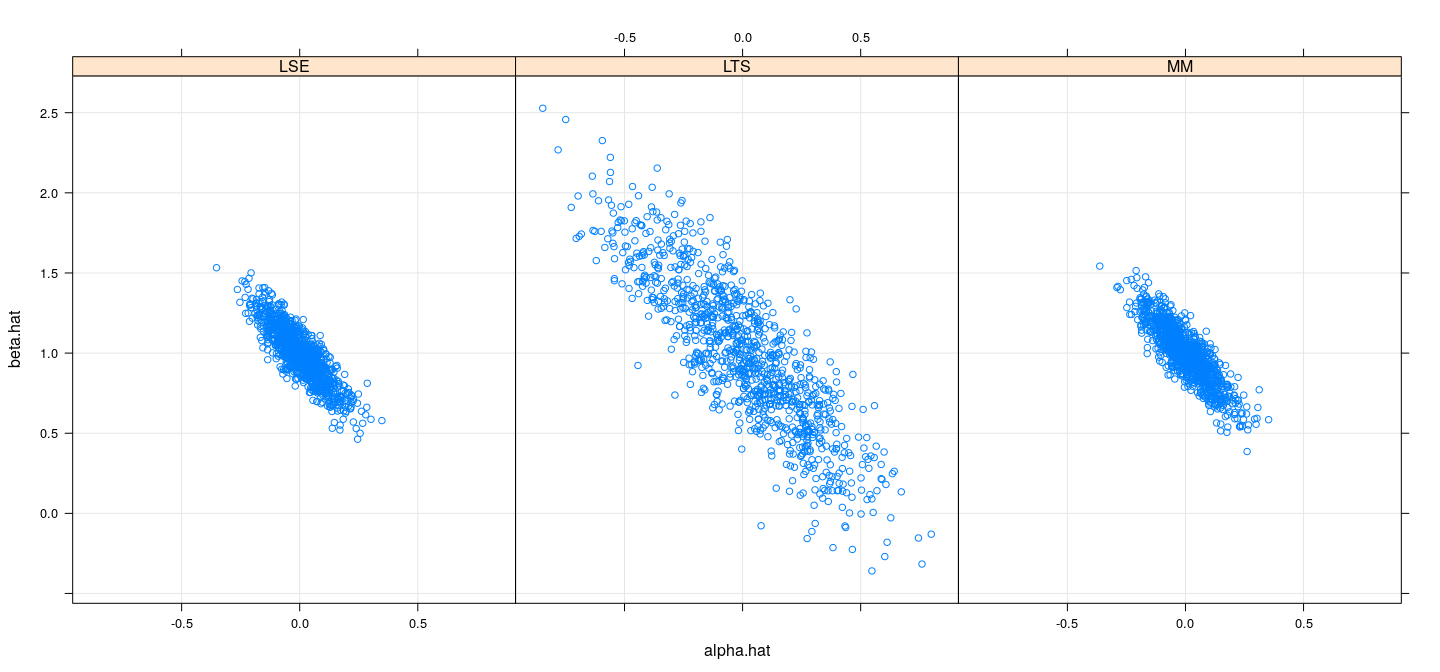
Efficiency comparison: simulation study (normal)
simulateCoefMM <- function(n)
{
x <- runif(n, 0, 1)
y <- x + 0.5 * rnorm(n)
fm1 <- lm(y ~ x)
fm2 <- rlm(y ~ x, method = "MM")
fm3 <- ltsreg(y ~ x)
data.frame(rbind(coef(fm1), coef(fm2), coef(fm3)),
model = c("LSE", "MM", "LTS"))
}
sim.coefsmm <- replicate(1000, simulateCoefMM(100), simplify = FALSE)
sim.coefsmm.df <- do.call(rbind, sim.coefsmm)
names(sim.coefsmm.df) <- c("alpha.hat", "beta.hat", "model")Efficiency comparison: simulation study (normal)
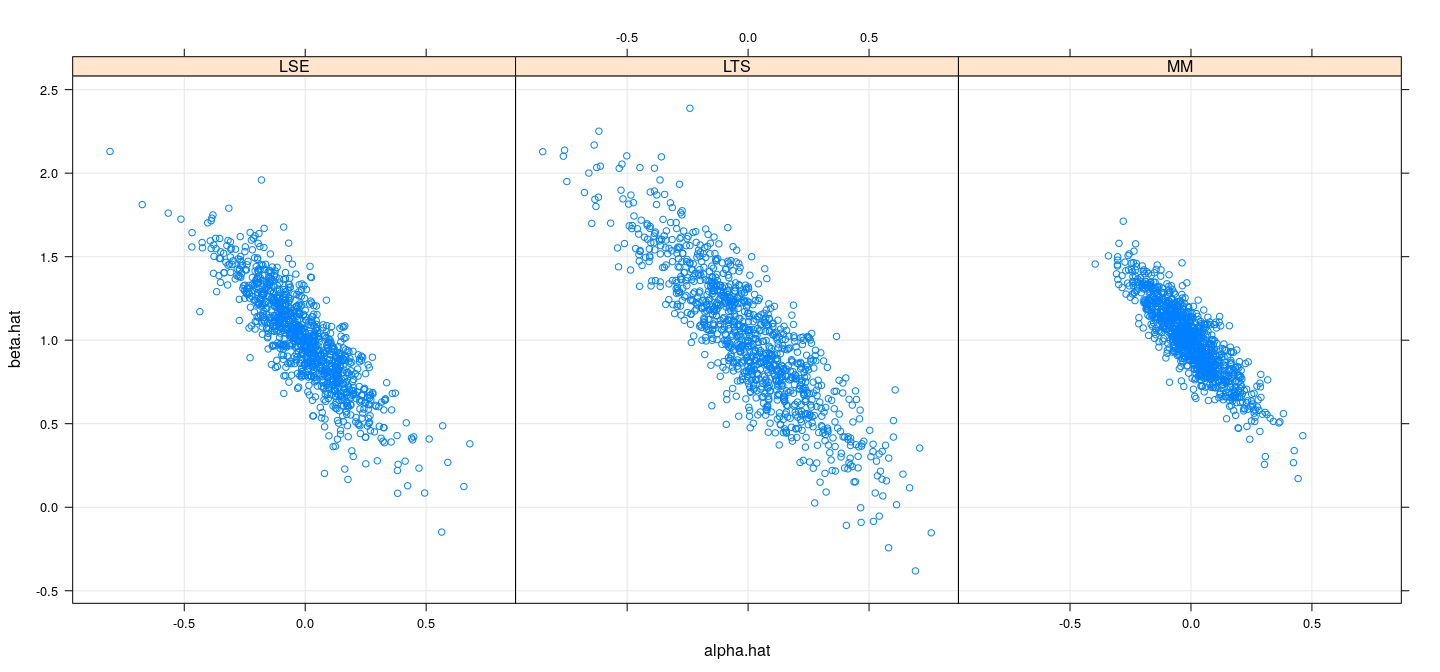
Efficiency comparison: simulation study (\(t_3\))
simulateCoefMMt <- function(n)
{
x <- runif(n, 0, 1)
y <- x + 0.5 * rt(n, df = 3)
fm1 <- lm(y ~ x)
fm2 <- rlm(y ~ x, method = "MM")
fm3 <- ltsreg(y ~ x)
data.frame(rbind(coef(fm1), coef(fm2), coef(fm3)),
model = c("LSE", "MM", "LTS"))
}
sim.coefsmmt <- replicate(1000, simulateCoefMMt(100), simplify = FALSE)
sim.coefsmmt.df <- do.call(rbind, sim.coefsmmt)
names(sim.coefsmmt.df) <- c("alpha.hat", "beta.hat", "model")Efficiency comparison: simulation study (\(t_3\))
Artificial example revisited
x <- c(1:10, 20)
y <- c(1:10 + rnorm(10, sd = 0.00001), 20 + 10)
fm.mm <- rlm(y ~ x, method = "MM")
fm.bs <- rlm(y ~ x, psi = psi.bisquare)
xyplot(y ~ x, pch = 16) + layer(panel.abline(fm.mm, col = "red")) + layer(panel.abline(fm.bs, col = "black"))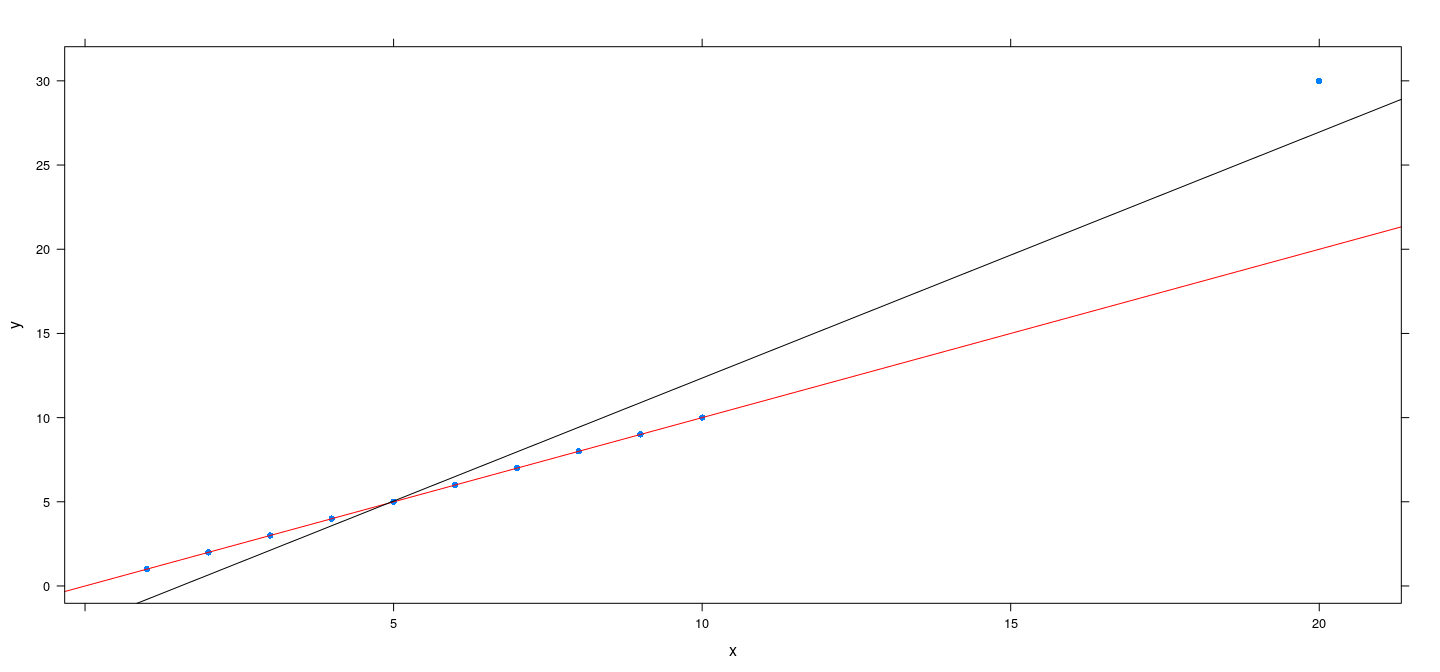
Software implementations in R
The
MASSpackage implements basic robust regression approachesFor more comprehensive implementations, see the Robust Statistical Methods Task View on CRAN