Early Prediction of COVID Surge

# Early Prediction of COVID Surge

## An Exercise in Exploratory Data Analysis

### Deepayan Sarkar

### _Indian Statistical Institute_

---

# Disclaimer

- This talk has very little "statistics" (in the conventional sense)

- The data analysis is based mostly on very simple ideas and models

- The emphasis of this talk is more on the _process_ than the outcome
--

- Also, it's important to remember that

]

---

# Outline

- What do we want to predict and why?

- Are we able to predict the past?

- How did we arrive at our method?

- Joint work with Siva Athreya and Rajesh Sundaresan

<div>
$$
\newcommand{\sub}{_}
\newcommand{\confirmed}[1]{x(#1)}
\newcommand{\active}[1]{a(#1)}
\newcommand{\dactive}[1]{a^{\prime}(#1)}
\newcommand{\dconfirmed}[1]{x^{\prime}(#1)}
\newcommand{\ractive}[1]{\lambda(#1)}
\newcommand{\ractivehat}[1]{\hat{\lambda}(#1)}
\newcommand{\rconfirmed}[1]{\gamma(#1)}
\newcommand{\rincrement}[1]{\rho(#1)}
\newcommand{\rincrementhat}[1]{\hat{\rho}(#1)}
\newcommand{\rinactive}[1]{\mu(#1)}
$$
</div>

[ Updated: 2022-02-16 ]

]

---

# What do we want to predict?

---

![plot of chunk dmb1](figures/predict-active-dmb1-1.png)

---

![plot of chunk dmb2](figures/predict-active-dmb2-1.png)

<!--

2021-04-09 26631
2021-04-15 54309

linc = diff(log(c(26631, 54309)))

91859 - max active - lower by same log

exp(log(91859) - linc) # potential gain in max active if lockdown had begun 1 week earlier

-->

---

# Question

- Could we have predicted (on March 15, say) that things are going to get this bad?
--

- We now know that INSACOG warned about variants of concern in early March

- But underlying data is not publicly available

---

# Question (rephrased)

- Could we have predicted (on March 15, say) that things are going to get this bad?

- ... using only publicly available data (daily new cases, active cases, recoveries, deaths)

---

# What should we predict exactly?

- How do we quantify prediction? For example:

- Is it useful to know the predicted number of cases two weeks from now?

- How do we act on such a number?
--

- We ended up with the following quantification:

__How long do we have till we hit limits of medical capacitity?__

]

- Here medical capacitity is represented by a critical number of _active_ cases

---

# Fast-forward: Would we have predicted the current surge?

---

![plot of chunk critical1](figures/predict-active-critical1-1.png)

---

![plot of chunk critical2](figures/predict-active-critical2-1.png)

---

# More results

- [Selected Indian Cities](#appendix)

- [Selected Indian States](active-prediction-state.html)

- [Selected Countries](active-prediction-bycountry.html)

- [Kerala](active-prediction-kerala.html)

- [Karnataka](active-prediction-karnataka.html)

- [West Bengal](active-prediction-wb.html)

- [Maharashtra](active-prediction-maharashtra.html)

---

# How did we arrive at these predictions?

---

# Goal

* Simple scheme to predict number of active cases
	
* Warning system based on zonewise ability to handle active cases

* Input requirements:

- Daily number of confirmed / active cases (available from state bulletins)
	
	- Critical number of active cases (to be determined policymakers)

* Output:

- Days to critical __at current rate of growth__

---

# Intuition

- If new cases exceed recoveries, active count will grow

- Key insight: Need to estimate _growth rate_

- Any "positive" growth rate will eventually lead to exponential growth

- Even more alarming if growth rate is increasing

---

# A crude estimate

- $t$ unit of time (in days)

- $\confirmed{t}$ is the total number of confirmed cases upto time $t$

- Estimate rate as ratio of new cases today and new cases yesterday:
  $$
  \rincrementhat{t} = \frac{x(t) - x(t-1)}{x(t-1) - x(t-2)}
  $$
--

- This is actually too noisy to be useful, so use one-week lag instead
  $$
  \rincrementhat{t} = \frac{x(t) - x(t-7)}{x(t-7) - x(t-14)}
  $$

---

![plot of chunk unnamed-chunk-4](figures/predict-active-unnamed-chunk-4-1.png)

---

![plot of chunk unnamed-chunk-5](figures/predict-active-unnamed-chunk-5-1.png)

---

# Smoothing

- $\rincrementhat{t}$ clearly changes with time

- Smoothing can be useful, but _ad hoc_ as no clear criterion
--

- We smooth the daily new confirmed case counts $\confirmed{t} - \confirmed{t-1}$

- Take square root first (counts are more like Poisson than Gaussian)

- Method: Smoothing spline with effective degrees of freedom set to $n^{1/2}$
	
	- The standard method to select tuning parameter (GCV) _does not_ work well

- The results shown are not meant for prediction

- For prediction: smoothing should be done only using data available up to prediction date

- We also need a more concrete model for reasonable predictions

---

# A more formal model

---

- $t$ unit of time (in days)

- $\confirmed{t}$ is the total number of confirmed cases upto time $t$

- $\active{t}$ is the total number of active cases at time $t$

- $\ractive{t}$ is the _number of new infections per active infection per unit time_ at time $t$

- __Can change with time__ .emph[ (this is a very important point) ]
	
	- Depends on many factors: .emph[ virus strain, social behaviour, vaccination ]

- Can be influenced by policy: .emph[ restriction on gatherings, lockdown ]

- $\rinactive{t}$ is the _number of deaths / recoveries
  per active infection per unit time_ at time $t$
  
    - Assumed constant: $\rinactive{t} \equiv 1/10$

- A simple evolution model: 
$$
\active{t + h} - \active{t} \approx h \cdot \active{t} \cdot [ \ractive{t} - \rinactive{t} ]
$$

---

- This gives an instantaneous definition of $\ractive{t}$ as
  $$
  \ractive{t} = \rinactive{t} + \frac{\dactive{t}}{\active{t}}
  $$
  
- For discrete-time data, we can estimate $\ractive{t}$ by
  $$
  \ractivehat{t} = \rinactive{t} + \frac{ \active{t + h} - \active{t} }{ h \cdot \active{t} }
  $$

- Smallest possible $h = 1$, but we use $h = 7$ to reduce day-of-the-week patterns — or smooth $\active{t}$
--

- Simpler than standard SIR models:

- Ignores changes in subpopulation fractions (infected, recovered, susceptible)

- These variations are subsumed in time-varying $\ractive{t}$

- The goal is to _warn_ when cases are _low_ (not to model full course)

<!--

- Alternative model 1: 
$$
\confirmed{t + h} - \confirmed{t} \approx h \cdot \active{t} \cdot \rconfirmed{t}
$$

- Estimate:
$$
\rconfirmed{t} = \frac{ \confirmed{t + h} - \confirmed{t} }{ h \cdot \active{t} }
$$

- Alternative model 2 (direct estimate from definition):
$$
\frac{\confirmed{t + h} - \confirmed{t}}{\confirmed{t} - \confirmed{t-h}} 
\approx h \cdot \active{t} \cdot \rincrement{t}
$$

- It turns out that $\ractive{t}$ and $\rincrement{t}$ behave
  similarly, $\rconfirmed{t}$ is a bit different

-->

---

![plot of chunk unnamed-chunk-6](figures/predict-active-unnamed-chunk-6-1.png)

---

![plot of chunk unnamed-chunk-7](figures/predict-active-unnamed-chunk-7-1.png)

---

# Key observations

- $\ractive{t}$ is __not__ constant

- Shows periodic stretches of growth and decline
	
- No systematic pattern
	
- Likely combination of biological (variants / vaccination) and social (behaviour) factors

- Difficult to predict

---

# Making predictions

---

- Prediction equations:

<div>
\begin{eqnarray*}
\active{s} &=& \active{s-h} + h \cdot \active{s-h} \, [ \ractivehat{s-h} - \rinactive{s-h} ] \\
&=& \active{s-h} \left( 1 + h \cdot [ \ractivehat{s-h} - \rinactive{s-h} ] \right)
\end{eqnarray*}
</div>

- Can take $h = 1$ for prediction

$$
\active{s+1} = \active{s} \left( 1 + \ractivehat{s} - \rinactive{s}  \right)
$$

- Question: How to estimate $\ractive{s}$ for future time $s$?

---

# Predicting $\ractive{s}$ for future time $s$

- Prediction can be meaningful only for short ranges

- We estimate $\ractive{s-h}$ as a linear function of $h$:

- Start from the last calculated value on date of prediction

- Linear slope estimated from the last two changes
	
- For robustness, we take average over last few values

- Start from average of last 4 calculated values of $\ractive{t}$ on date of prediction

- Linear slope estimated using linear regression of last 5 estimates

- Note that

- $\ractive{s} > 0.1$ implies active cases will _increase_ over time

- $\ractive{s} < 0.1$ implies active cases will _decrease_ over time

<!--

- Other models can similarly predict $\active{t}$

- But this seems most stable (TODO: re-check implementations), so only one reported here

-->

---

# Example: How soon would this have predicted the Delhi wave?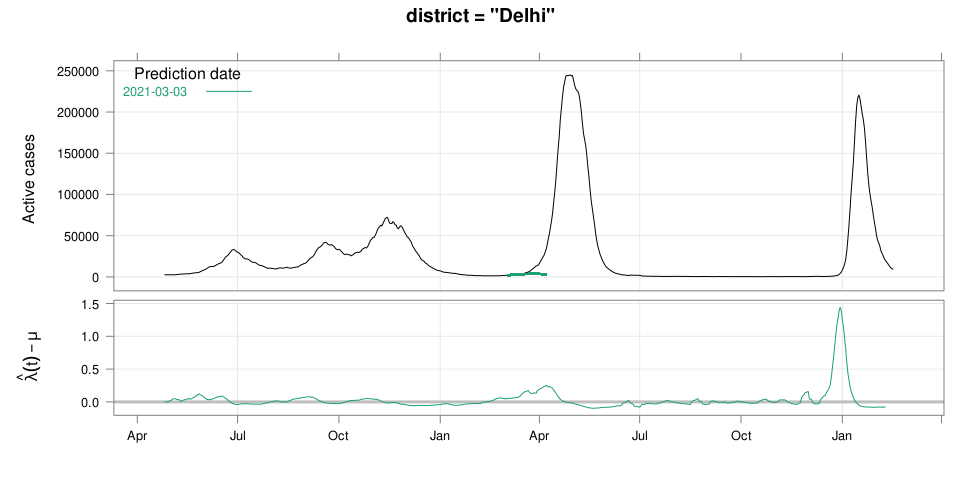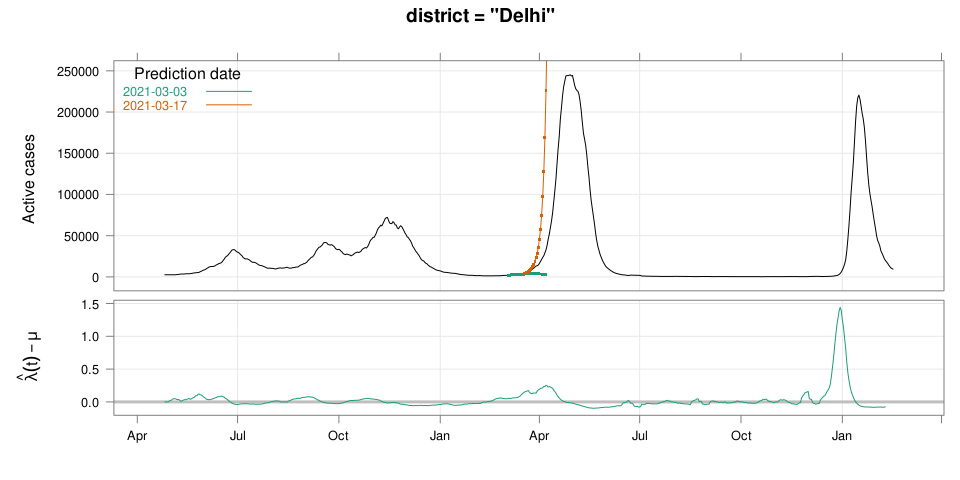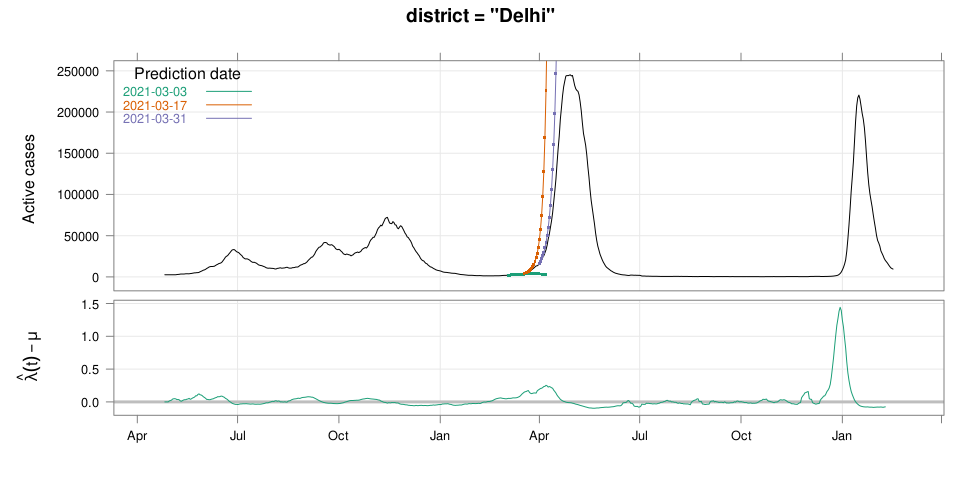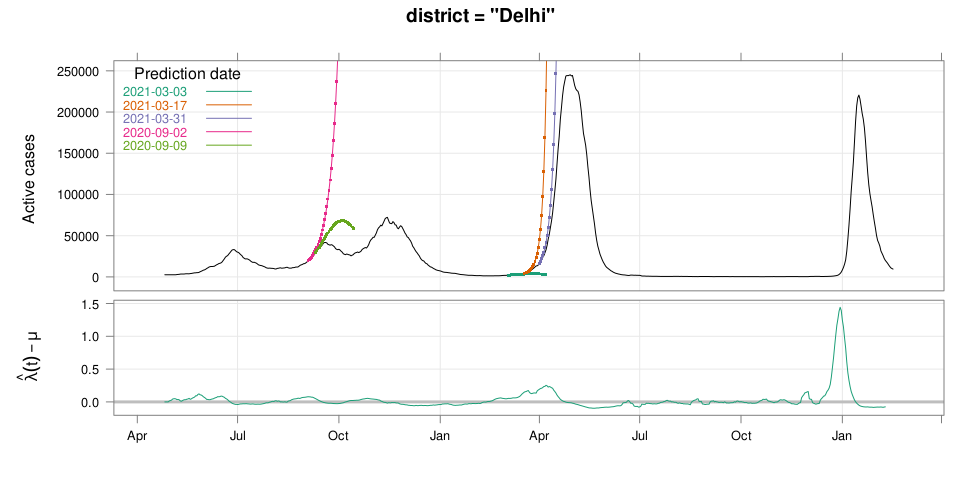

---

![plot of chunk delhipred1](figures/predict-active-delhipred1-1.png)

---

![plot of chunk delhipred2](figures/predict-active-delhipred2-1.png)

---

![plot of chunk delhipred3](figures/predict-active-delhipred3-1.png)

---

![plot of chunk delhipred4](figures/predict-active-delhipred4-1.png)

---

- Predictions can change dramatically over the course of a few days
	
- Long-range predictions should _not_ be taken too seriously (linear growth unrealistic)
	
- More important to track $\ractive{t}$
	
- However, local trends in $\ractive{t}$ __can__ give early warning
	
	- Can indicate upcoming surge
	
	- Can detect upcoming peaks (inflection points)
	
	- Trends easier to spot than from plot of raw active counts

---

# Early warning: days till _critical load_

---

- A more useful daily summary: number of days to reach critical target

- Needs more information: zonewise medical capacity

- We will just use target = 100000

- Number of days is capped at 150 (larger values are plotted as 150)

---

![plot of chunk delhipredcritical](figures/predict-active-delhipredcritical-1.png)

---

- Gives early warning, but also .emph[ lots of false positives ]

- Alternative: Assume that $\ractive{s}$ remains .emph[ constant ] in the short run

- More conservative predictions, less false alarms

---

# Conservative prediction using constant $\ractive{t}$

---

![plot of chunk delhipredcriticalconst](figures/predict-active-delhipredcriticalconst-1.png)

---

# Does smoothing help? (without looking ahead)

---

![plot of chunk unnamed-chunk-8](figures/predict-active-unnamed-chunk-8-1.png)

---

![plot of chunk unnamed-chunk-9](figures/predict-active-unnamed-chunk-9-1.png)

---

# Summary: Prepare for the next surge

* Current data can predict time to resource scarcity

* Estimates are only approximate, but good enough for early warning

* Can be used to guide poilcy:

- Graded response can strike balance between normal life and adverse health outcomes
	
	- Prevent unnecessary economic slowdown (due to restrictions)
	
	- Prevent avoidable deaths (due to lack of basic medical facilities)

* Obvious strategies: vaccinate, ramp up healthcare facilities
	
* But need to be prepared for surge (new mutations, loss of immunity, unknown factors)
	
* Late reaction leaves lockdown as only solution, cannot prevent deaths
--

* .emph[ Recommendation: ] Automatic restrictions based on current growth rate

---

# Other possible uses

- Short-term predictions (e.g., [Delhi](Delhi.pdf), [Karnataka](Karnataka.pdf))

- Retrospective study of growth timeline (e.g., [compare urban / rural spread](https://deepayan.github.io/covid-19/increment-ratio.html#11))

- Extend more sophisticated models (e.g. SUTRA)

- Key insight: parameters must be estimated _adaptively_
	
	- Smoothing may help

---

# Appendix: Predictions in selected Indian cities

("critical" load based on past history)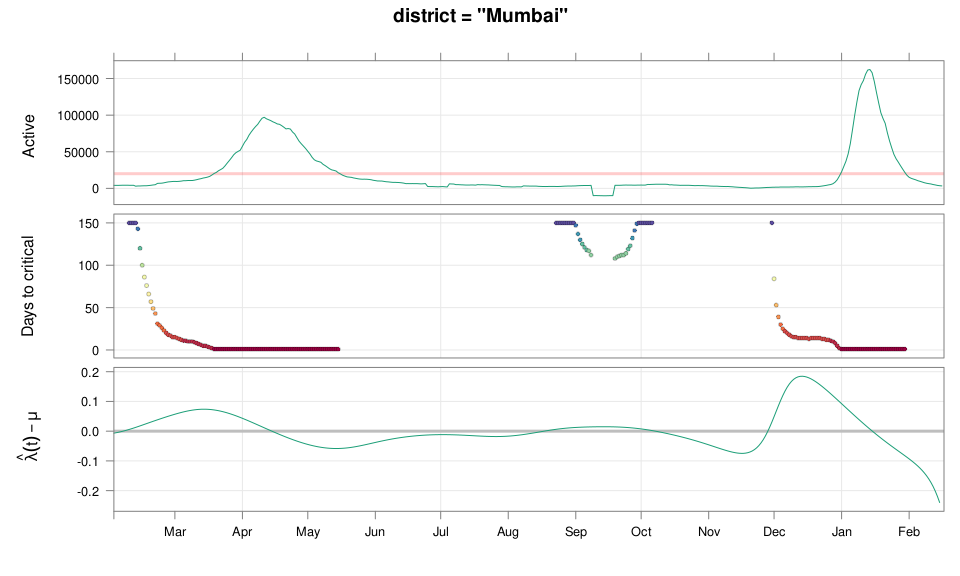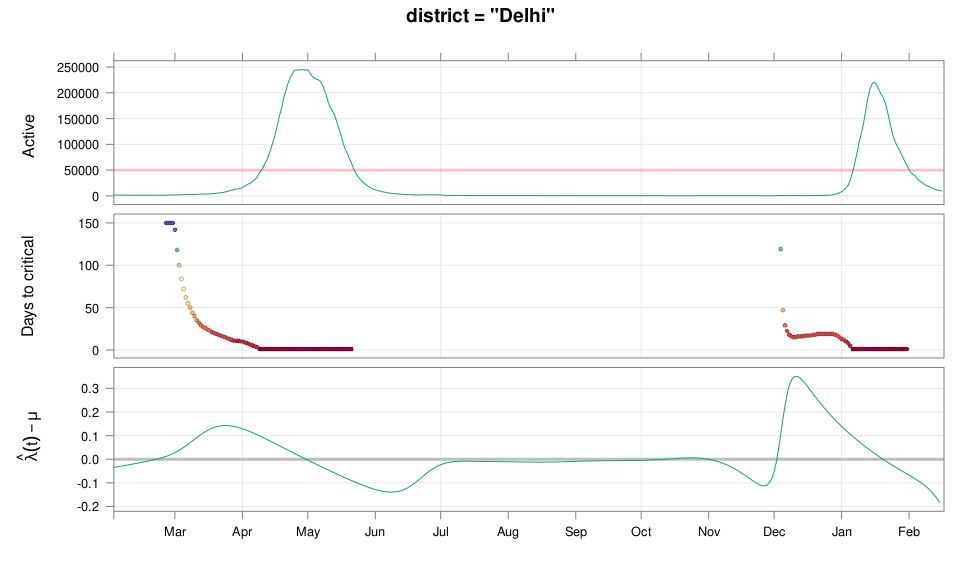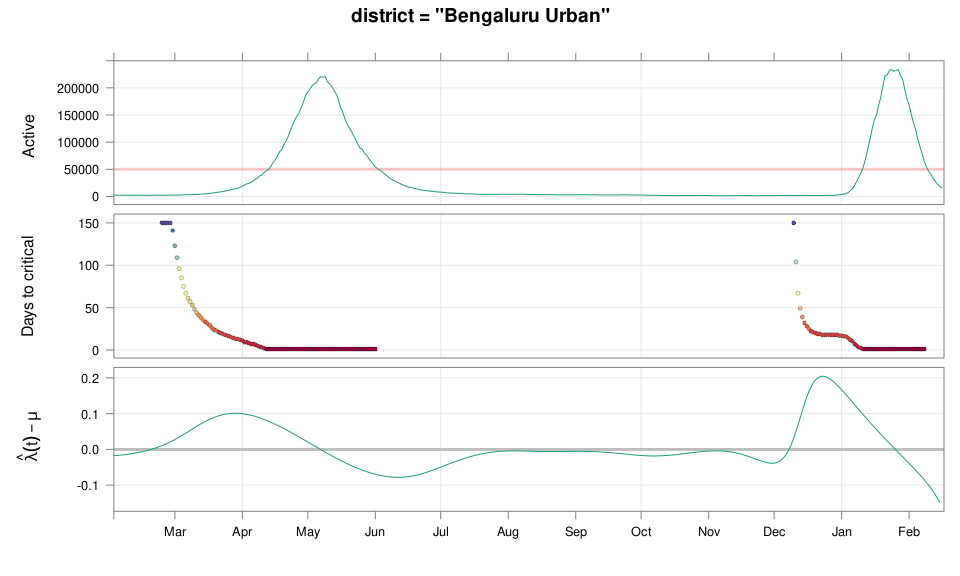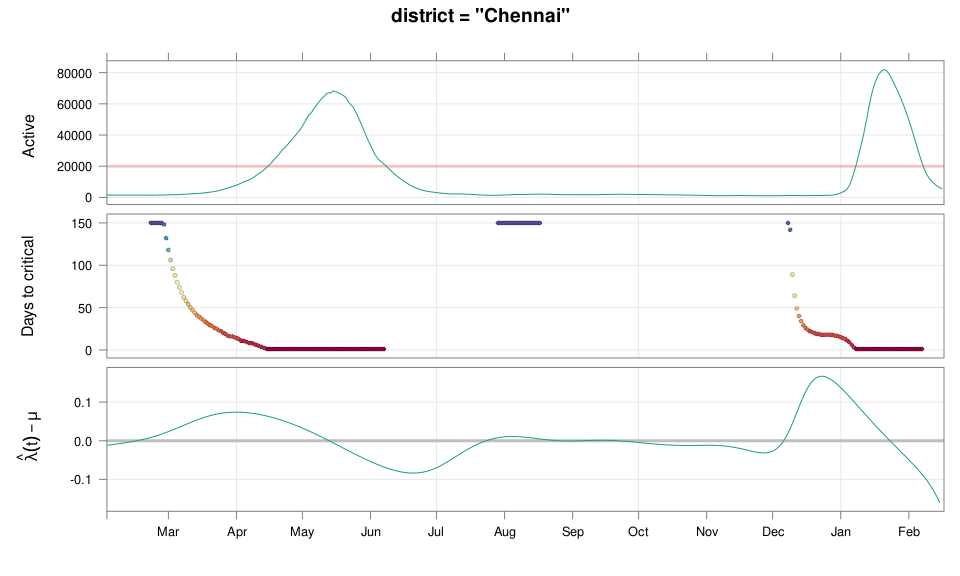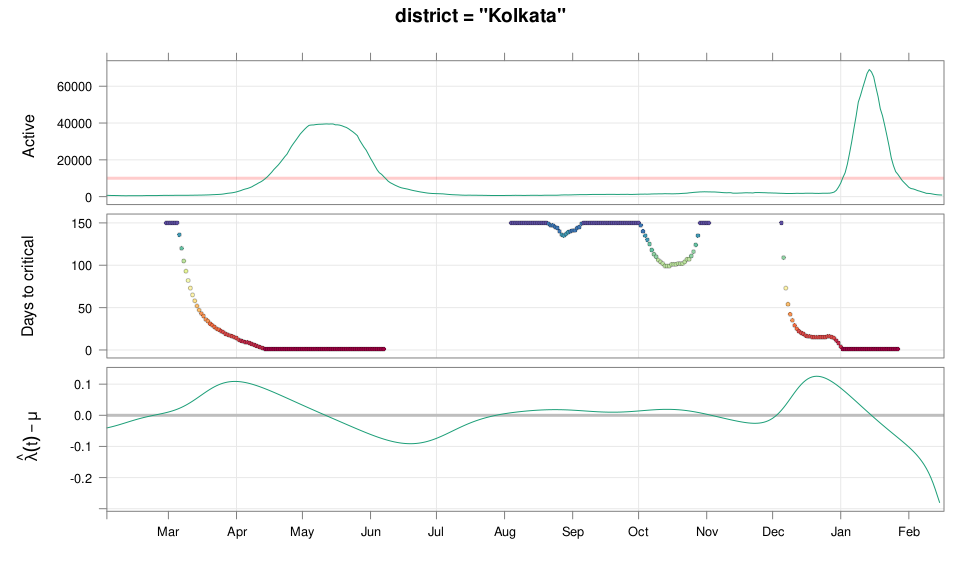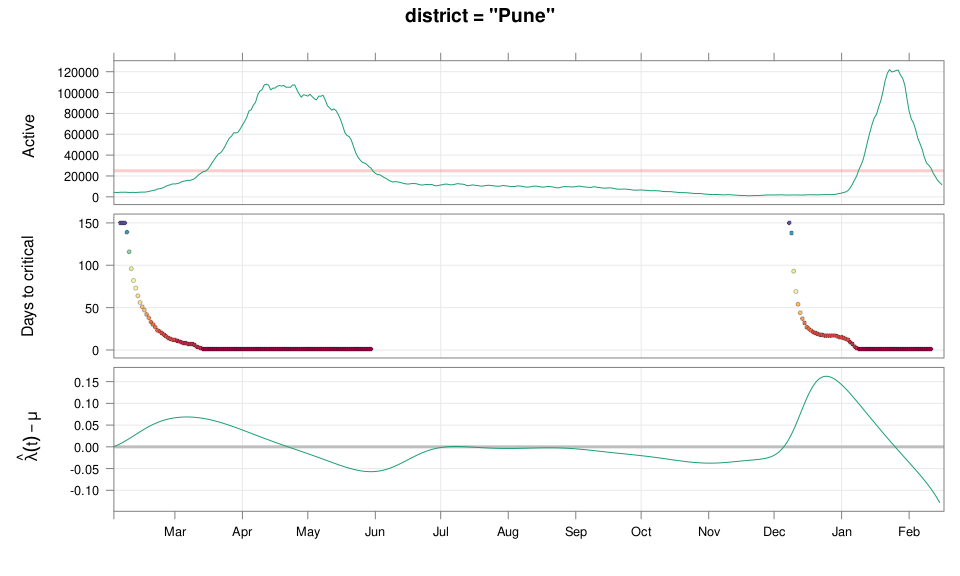

---

![plot of chunk mumbaicritical](figures/predict-active-mumbaicritical-1.png)

---

![plot of chunk delhicritical](figures/predict-active-delhicritical-1.png)

---

![plot of chunk bengalurucritical](figures/predict-active-bengalurucritical-1.png)

---

![plot of chunk chennaicritical](figures/predict-active-chennaicritical-1.png)

---

![plot of chunk kolkatacritical](figures/predict-active-kolkatacritical-1.png)

---

![plot of chunk punecritical](figures/predict-active-punecritical-1.png)

---

---