Writing R Functions

Deepayan Sarkar

Functions in R

  • A tutorial on R would be incomplete without a discussion of functions

  • R provides most of its functionality through functions

  • However, it by design does not try to provide functions to satisfy all needs

  • R users are expected to write their own functions to suit their requirements

Functions are “first class” objects in R

  • From a language perspective, functions are like any other type of object

  • They can be bound to variables, and put inside lists

  • They can be passed as arguments to other functions

  • In fact, this is very common, and we will see many such examples

Creating functions

  • Functions are created using the following structure:

  • Here args is a comma-separated list of variables (arguments) that are available to the function

  • The instructions are R code that is executed whenever the function is run

  • Every function must return a value

  • The return value can be explicit using return(), otherwise it is the last evaluated expression

  • See help("function") (note that the quotes are required)

  • Without going into technical detail, we will learn through examples

  • Functions can be very simple. For example:

    • We are interested in the p-value for many of the tests we do

    • However, R doesn’t have a function that provides just the p-value

    • To extract the p-value from a test, we need to know its internal structure

  • We can define a function to extract p-values as follows:

  • Let’s read in the demog data again:
'data.frame':   60 obs. of  5 variables:
 $ subjid: int  101 102 103 104 105 106 201 202 203 204 ...
 $ trt   : Factor w/ 2 levels "Active","Placebo": 2 1 1 2 1 2 1 2 1 2 ...
 $ gender: Factor w/ 2 levels "Male","Female": 1 2 1 2 1 2 1 2 1 2 ...
 $ race  : Factor w/ 3 levels "White","Black",..: 3 1 2 1 3 1 3 1 2 1 ...
 $ age   : int  37 65 32 23 44 49 35 50 49 60 ...
  • And extract the p-values for various tests
[1] 0.7155171
[1] 0.7155208
[1] 0.2910557
[1] 0.4035804
NULL

p-value for linear models

  • Our function doesn’t work for lm() fits

  • This is because "lm" objects do not store a p-value as the $p.value component

  • In fact, a linear model can lead to many tests, and it is not clear which p-value should be reported

  • It is conventional to report the p-value of the test comparing full model with intercept-only model

  • This is shown as the last result in summary()


Call:
lm(formula = age ~ race, data = demog)

Residuals:
    Min      1Q  Median      3Q     Max 
-29.722  -7.722  -2.389  10.528  28.611 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   52.722      2.185  24.133   <2e-16 ***
raceBlack     -4.333      3.784  -1.145    0.257    
raceOther     -6.722      5.780  -1.163    0.250    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 13.11 on 57 degrees of freedom
Multiple R-squared:  0.03695,   Adjusted R-squared:  0.003158 
F-statistic: 1.093 on 2 and 57 DF,  p-value: 0.342
  • However, it can be quite frustrating to figure out where this p-value is calculated
List of 11
 $ call         : language lm(formula = age ~ race, data = demog)
 $ terms        :Classes 'terms', 'formula'  language age ~ race
  .. ..- attr(*, "variables")= language list(age, race)
  .. ..- attr(*, "factors")= int [1:2, 1] 0 1
  .. .. ..- attr(*, "dimnames")=List of 2
  .. .. .. ..$ : chr [1:2] "age" "race"
  .. .. .. ..$ : chr "race"
  .. ..- attr(*, "term.labels")= chr "race"
  .. ..- attr(*, "order")= int 1
  .. ..- attr(*, "intercept")= int 1
  .. ..- attr(*, "response")= int 1
  .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
  .. ..- attr(*, "predvars")= language list(age, race)
  .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "factor"
  .. .. ..- attr(*, "names")= chr [1:2] "age" "race"
 $ residuals    : Named num [1:60] -9 12.3 -16.4 -29.7 -2 ...
  ..- attr(*, "names")= chr [1:60] "1" "2" "3" "4" ...
 $ coefficients : num [1:3, 1:4] 52.72 -4.33 -6.72 2.18 3.78 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:3] "(Intercept)" "raceBlack" "raceOther"
  .. ..$ : chr [1:4] "Estimate" "Std. Error" "t value" "Pr(>|t|)"
 $ aliased      : Named logi [1:3] FALSE FALSE FALSE
  ..- attr(*, "names")= chr [1:3] "(Intercept)" "raceBlack" "raceOther"
 $ sigma        : num 13.1
 $ df           : int [1:3] 3 57 3
 $ r.squared    : num 0.0369
 $ adj.r.squared: num 0.00316
 $ fstatistic   : Named num [1:3] 1.09 2 57
  ..- attr(*, "names")= chr [1:3] "value" "numdf" "dendf"
 $ cov.unscaled : num [1:3, 1:3] 0.0278 -0.0278 -0.0278 -0.0278 0.0833 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:3] "(Intercept)" "raceBlack" "raceOther"
  .. ..$ : chr [1:3] "(Intercept)" "raceBlack" "raceOther"
 - attr(*, "class")= chr "summary.lm"

  • It turns out that the calculation is done in the print() method for "summary.lm" objects

  • The following shows the relevant part of the method

    ...
    if (!is.null(x$fstatistic)) {
        cat("Multiple R-squared: ", formatC(x$r.squared, digits = digits))
        cat(",\tAdjusted R-squared: ", formatC(x$adj.r.squared, 
            digits = digits), "\nF-statistic:", formatC(x$fstatistic[1L], 
            digits = digits), "on", x$fstatistic[2L], "and", 
            x$fstatistic[3L], "DF,  p-value:", format.pval(pf(x$fstatistic[1L], 
                x$fstatistic[2L], x$fstatistic[3L], lower.tail = FALSE), 
                digits = digits))
        cat("\n")
    }
   ...

How does this help us?

  • A more flexible design for our pvalue() function:

    • Make the function generic

    • Write specific methods for "htest" and "lm" objects

    • Other types of objects can be supported in future by adding suitable methods

Generic function with methods

[1] 0.7155171
[1] 0.7155208
[1] 0.2910557
[1] 0.4035804
    value 
0.3419768

Inspecting functions

  • All R functions are defined in essentially the same manner

  • Just like other variables, functions can also be printed

  • Typing the name of a funtion will usually display its definition

  • Some functions call C / Fortran code, which will show up as .Primitive(), .Internal(), .Call(), etc.

function (x, ...)  .Primitive("rep")
function (x, decreasing = FALSE, ...) 
{
    if (!is.logical(decreasing) || length(decreasing) != 1L) 
        stop("'decreasing' must be a length-1 logical vector.\nDid you intend to set 'partial'?")
    UseMethod("sort")
}
<bytecode: 0x55ffede5fce0>
<environment: namespace:base>
function (x, decreasing = FALSE, na.last = NA, ...) 
{
    if (is.object(x)) 
        x[order(x, na.last = na.last, decreasing = decreasing)]
    else sort.int(x, na.last = na.last, decreasing = decreasing, 
        ...)
}
<bytecode: 0x55ffee708208>
<environment: namespace:base>
function (..., na.last = TRUE, decreasing = FALSE, method = c("auto", 
    "shell", "radix")) 
{
    z <- list(...)
    decreasing <- as.logical(decreasing)
    if (length(z) == 1L && is.numeric(x <- z[[1L]]) && !is.object(x) && 
        length(x) > 0) {
        if (.Internal(sorted_fpass(x, decreasing, na.last))) 
            return(seq_along(x))
    }
    method <- match.arg(method)
    if (any(vapply(z, is.object, logical(1L)))) {
        z <- lapply(z, function(x) if (is.object(x)) 
            as.vector(xtfrm(x))
        else x)
        return(do.call("order", c(z, list(na.last = na.last, 
            decreasing = decreasing, method = method))))
    }
    if (method == "auto") {
        useRadix <- all(vapply(z, function(x) {
            (is.numeric(x) || is.factor(x) || is.logical(x)) && 
                is.integer(length(x))
        }, logical(1L)))
        method <- if (useRadix) 
            "radix"
        else "shell"
    }
    if (method != "radix" && !is.na(na.last)) {
        return(.Internal(order(na.last, decreasing, ...)))
    }
    if (method == "radix") {
        decreasing <- rep_len(as.logical(decreasing), length(z))
        return(.Internal(radixsort(na.last, decreasing, FALSE, 
            TRUE, ...)))
    }
    if (any(diff((l.z <- lengths(z)) != 0L))) 
        stop("argument lengths differ")
    na <- vapply(z, is.na, rep.int(NA, l.z[1L]))
    ok <- if (is.matrix(na)) 
        rowSums(na) == 0L
    else !any(na)
    if (all(!ok)) 
        return(integer())
    z[[1L]][!ok] <- NA
    ans <- do.call("order", c(z, list(decreasing = decreasing)))
    ans[ok[ans]]
}
<bytecode: 0x55ffed412388>
<environment: namespace:base>

Another example: linear regression

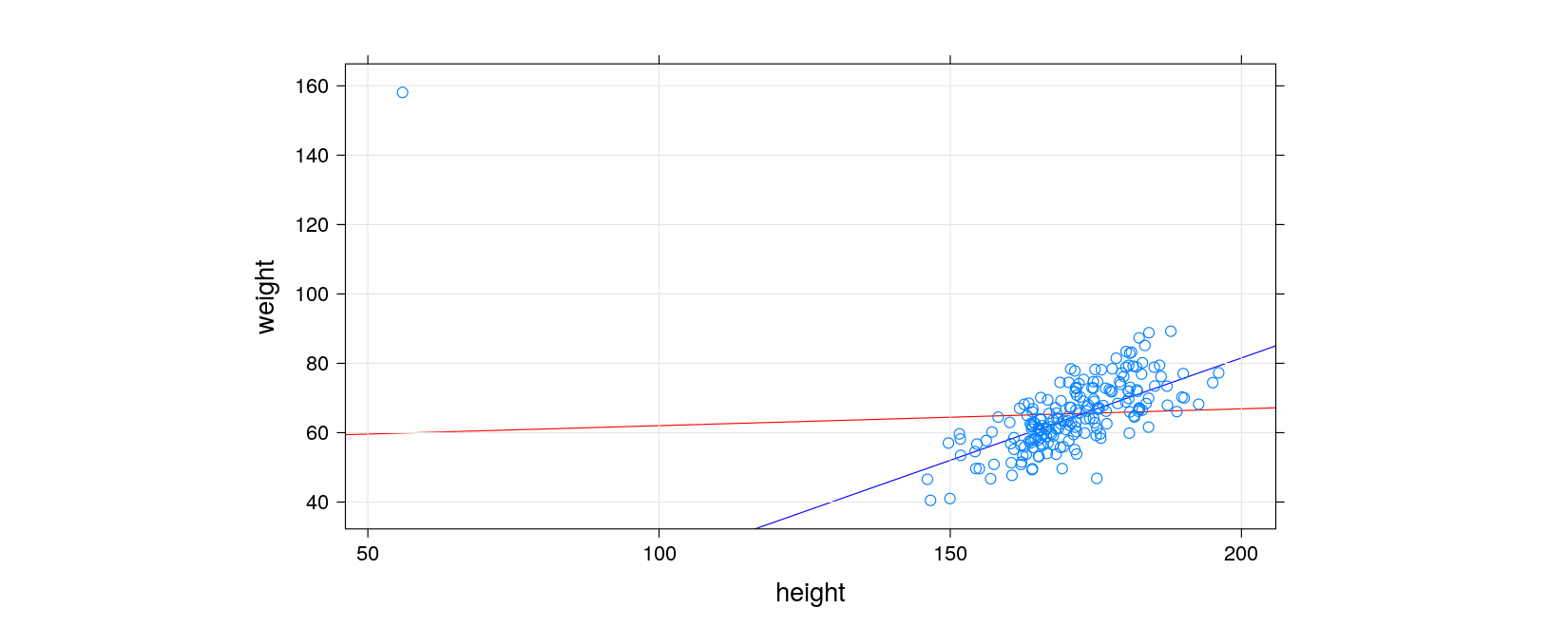
  • Recall our simulated height-weight example
  • Suppose we further switch the height and weight of the first observation
'data.frame':   200 obs. of  3 variables:
 $ height: num  56 166 167 160 172 ...
 $ bmi   : num  22.4 20.5 21.3 22.1 18.3 ...
 $ weight: num  158.1 56.3 59.7 56.8 53.8 ...

Call:
lm(formula = weight ~ height, data = htwt)

Coefficients:
(Intercept)       height  
   57.21366      0.04832
  • Recall that we can also obtain the coefficients by explicitly solving the regression equations
           [,1]
Int 57.21366290
HT   0.04832182

  • Yet another conceptually equivalent method is to minimize the sum of squared errors

  • R has several general-purpose optimizers, typically used through optim()

  • At a minimum, optim() requires a function to be optimized and a starting estimate

  • Here, our “sum-of-squares” function takes a parameter of length-2

$par
[1] 57.17301085  0.04852863

$value
[1] 25122.54

$counts
function gradient 
     121       NA 

$convergence
[1] 0

$message
NULL
  • The benefit of this approach is that we can easily change the objective function
$par
[1] -36.4945566   0.5902061

$value
[1] 1193.13

$counts
function gradient 
     149       NA 

$convergence
[1] 0

$message
NULL

This is an example of robust regression

plot of chunk unnamed-chunk-16

The *apply() family of functions

  • Notice that the second argument of optim() above is a function

  • Another useful class of functions taking other functions as argument: various apply() type functions

  • The most general-purpose among these is lapply(), which applies a function on all elements of a list

$height
[1] 171.0055

$bmi
[1] 21.98674

$weight
[1] 64.49612
  • We can also provide a user-defined function here:
$height
    mean   median 
170.8390 171.0055 

$bmi
    mean   median 
22.07640 21.98674 

$weight
    mean   median 
65.46891 64.49612

  • In fact, the function doesn’t need to have a name

  • Such functions defined in-place are known as anonymous functions

$height
      SD      IQR 
12.45180 13.43753 

$bmi
      SD      IQR 
2.164412 3.100270 

$weight
      SD      IQR 
11.25193 12.98609
  • This is useful in conjunction with split() to compute per-group summaries
List of 2
 $ Active : int [1:31] 65 32 44 35 49 39 67 65 36 44 ...
 $ Placebo: int [1:29] 37 23 49 50 60 70 55 45 46 77 ...
$Active
[1] 51.35484

$Placebo
[1] 50.10345
  Active  Placebo 
51.35484 50.10345
  • In fact, this is so common that there is a function called tapply() to make this easier
  Active  Placebo 
51.35484 50.10345


  • A related function called apply() is used to apply a function on rows or columns of a matrix

  • We will use these concepts frequently in the remainder of the workshop