- ... otherwise1
- Bernal [1991] gives a detailed account of this fabrication of Eurocentrism.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2
- For a comprehensive discussion of the mathematics found in the Babylonian tablets see Ifrah [2000].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... system3
- Notation:-
 denotes
the number
denotes
the number
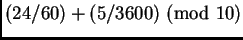 , while
, while
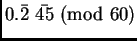 denotes
denotes
 . In the next section we discuss how the Babylonians used
. In the next section we discuss how the Babylonians used  as a place marker.
as a place marker.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... steps4
- The Babylonians were not afraid of taking squares as has been attested by the fact that many tablets have been discovered of squares. In fact their multiplication was based on the formula
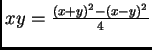 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... square5
- Note that Ifrah [2000] makes a mistake in obtaining these relations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... number6
- Note that if someone says that she spent sarhe teen (Hindi)
to buy a car, then we'd immediately realise that she spent Rs. 3.5 lakhs for the car, on the other hand, if she spent sarhe teen for buying samosas then she bought only
Rs 3.50 worth of samosas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... influence''7
- This argument being rather technical we do not reproduce it here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... allowed8
- Many suggest that this could be because of the rejection by Indian mathematicians of this period of the Greek method of proof, which nowadays every school child knows as reductio ad absurdum. Indeed, assuming
Bhaskara's use of division by zero to be correct we obtain
that
 ; hence
; hence
 and so
and so 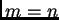 - a contradiction.
- a contradiction.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integer9
- In a sense, when L'Hôpital looks at
 with
with 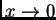 he is visiting this old conundrum
he is visiting this old conundrum
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
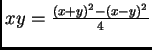 .
.