Penalized Regression

Deepayan Sarkar

Penalized regression

  • Another potential remedy for collinearity

  • Decreases variability of estimated coefficients at the cost of introducing bias

  • Also known as regularization

  • Important beyond the collinearity context

    • Certain types of penalties can be used for variable selection in a natural way

    • Penalized regression provides solutions in ill-posed (rank-deficient) problems

    • Familiar examples of such models are ANOVA models with all dummy variables

    • A more realistic situation is models with \(p > n\) (more covariates than observations)

Penalized likelihood and Bayesian interpretation

  • We have already seen an example of penalized regression: smoothing splines

  • Given data \(\{ (x_i, y_i ) : x_i \in [a, b] \}\), goal is to find \(f\) that minimizes (given \(\lambda > 0\))

\[ \sum_i (y_i - f(x_i))^2 + \lambda \int_{a}^{b} (f^{\prime\prime}(t))^2 dt \]

  • The solution is a natural cubic spline

  • Here \(f\) is the parameter of interest

  • The (ill-posed) least squares problem is regularized by adding a penalty for “undesirable” (wiggly) solutions

  • The same idea can be applied for usual (finite-dimensional) parameters as well

Penalized likelihood and Bayesian interpretation

  • Penalized regression is a special case of the more general penalized likelihood approach

  • This is easiest to motivate using a Bayesian argument

  • Consider unknown parameter \(\theta\) and observed data \(y\) with

\[\begin{eqnarray*} \theta &\sim& p(\theta) \quad\quad \text{ (prior) } \\ y | \theta &\sim& p(y | \theta) \end{eqnarray*}\]


  • Bayesian inference is based on the posterior distribution of \(\theta\), given by

\[ p(\theta | y) = \frac{p(\theta, y)}{p(y)} = \frac{p(\theta) \, p(y | \theta)}{p(y)} \]

  • Here \(p(y)\) is the marginal density of \(y\) given by

\[ p(y) = \int p(\theta) \, p(y | \theta) \, d\theta \]

Penalized likelihood and Bayesian interpretation

  • How does posterior \(p(\theta | y)\) lead to inference on \(\theta\)?

  • We could look at \(E(\theta | y)\), \(V(\theta | y)\), etc.

  • We could also look at the maximum-a-posteriori (MAP) estimator

\[ \hat\theta = \arg \max_{\theta} p(\theta | y) \]

  • This is analagous to MLE in the classical frequentist setup

  • Unfortunately, \(p(y)\) is in general difficult to compute

  • This has led to methods to simulate from \(p(\theta | y)\) without knowing \(p(y)\) (MCMC)

Penalized likelihood and Bayesian interpretation

  • Fortunately, MAP estimation does not require \(p(y)\), which does not depend on \(\theta\)

  • \(\hat\theta\) is given by

\[\begin{eqnarray*} \hat\theta &=& \arg \max_{\theta}\, p(\theta | y) \\ &=& \arg \max_{\theta}\, \frac{ p(\theta) \, p(y | \theta) }{ p(y) } \\ &=& \arg \max_{\theta}\, p(y | \theta) \, p(\theta) \\ &=& \arg \max_{\theta}\, [ \log p(y | \theta) + \log p(\theta) ] \end{eqnarray*}\]

  • The first term is precisely the usual log-likelihood

  • The second term can be viewed as a “regularization penalty” for “undesirable” \(\theta\)

Penalized regression: normal linear model with normal prior

  • Assume the usual normal linear model

\[ \mathbf{y} | \mathbf{X}, \beta \sim N( \mathbf{X} \beta, \sigma^2 \mathbf{I}) \]

  • Addidionally, assume an i.i.d. mean-zero normal prior for each \(\beta_j\)

\[ \beta \sim N( \mathbf{0}, \tau^2 \mathbf{I}) \]

  • Then it is easy to see that if \(L\) is the penalized log-likelihood, then

\[ -2 L(\beta) = C(\sigma^2, \tau^2) + \frac{1}{\sigma^2} \sum_{i=1}^n (y_i - \mathbf{x}_i^T \beta)^2 + \frac{1}{\tau^2} \sum_{j=1}^p \beta_j^2 \]

  • Thus, the MAP estimate of \(\beta\) is (as a function of the unknown \(\sigma^2\) and “prior parameter” \(\tau^2\))

\[ \hat\beta = \arg \min_{\beta}\, \sum_{i=1}^n (y_i - \mathbf{x}_i^T \beta)^2 + \frac{\sigma^2}{\tau^2} \sum_{j=1}^p \beta_j^2 \]

Ridge regression

  • This is known as Ridge regression, with the problem defined in terms of the “tuning parameter” \(\lambda\)

\[ \hat\beta = \arg \min_{\beta}\, \sum_{i=1}^n (y_i - \mathbf{x}_i^T \beta)^2 + \lambda \sum_{j=1}^p \beta_j^2 \]

  • As discussed earlier, this approach does not really make sense unless columns of \(\mathbf{X}\) are standardized

  • It is also not meaningful to penalize the intercept

  • For these reasons, in what follows, we assume without loss of generality that

    • Columns of \(\mathbf{X}\) have been centered and scaled to have mean \(0\) and variance \(1\)

    • \(\mathbf{y}\) has been centered to have mean 0

    • The model is fit without an intercept (which is separately estimated as \(\bar{y}\))

  • In practice, these issues are usually handled by model fitting software in the background

Ridge regression: solution

  • It is easy to see that the objective function to be minimized is

\[ \mathbf{y}^T \mathbf{y} + \beta^T \mathbf{X}^T \mathbf{X} \beta - 2 \mathbf{y}^T \mathbf{X} \beta + \lambda \beta^T \beta = \mathbf{y}^T \mathbf{y} + \beta^T (\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I}) \beta - 2 \mathbf{y}^T \mathbf{X} \beta \]

  • The corresponding normal equations are

\[ (\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I}) \beta = \mathbf{X}^T \mathbf{y} \]

  • This gives the Ridge estimator

\[ \hat{\beta} = (\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I})^{-1} \mathbf{X}^T \mathbf{y} \]

  • Note that \(\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I}\) is always invertible

  • To prove this, use the singular value decomposition of \(\mathbf{X}^T \mathbf{X} = \mathbf{A} \mathbf{\Lambda} \mathbf{A}^T\)

\[ \mathbf{X}^T \mathbf{X} + \lambda \mathbf{I} = \mathbf{A} (\mathbf{\Lambda} + \lambda \mathbf{I}) \mathbf{A}^T \]

  • Even if \(\mathbf{\Lambda}\) has some zero diagonal entries, all diagonal entries of \(\mathbf{\Lambda} + \lambda \mathbf{I}\) are at least \(\lambda\)

Ridge regression: solution

  • As \(\lambda \to 0\), \(\hat{\beta}_{ridge} \to \hat{\beta}_{OLS}\)

  • As \(\lambda \to \infty\), \(\hat{\beta}_{ridge} \to \mathbf{0}\)

  • In the special case where columns of \(\mathbf{X}\) are orthogonal (\(\mathbf{A} = \mathbf{I}\))

\[ \hat{\beta}_{ridge} = \frac{1}{1+\lambda} \hat{\beta}_{OLS} \]

  • This illustates the essential feature of ridge regression: shrinkage towards \(0\) (the prior mean of \(\beta\))

  • The ridge penalty introduces bias by shrinkage but reduces variance

Ridge regression in the presence of collinearity

  • Recall our experiment with simulated collinearity

Call:
lm(formula = y ~ ., data = d3)

Coefficients:
(Intercept)           x1           x2           x3  
    -0.3256       0.7419       1.8612       0.1909

Ridge regression in the presence of collinearity

                   x1         x2         x3 
-0.3339996  0.1511181  1.2421567  0.7907122 
                     x1          x2          x3 
-0.34263086  0.01199235  1.03851408  0.89352016


Ridge regression in the presence of collinearity

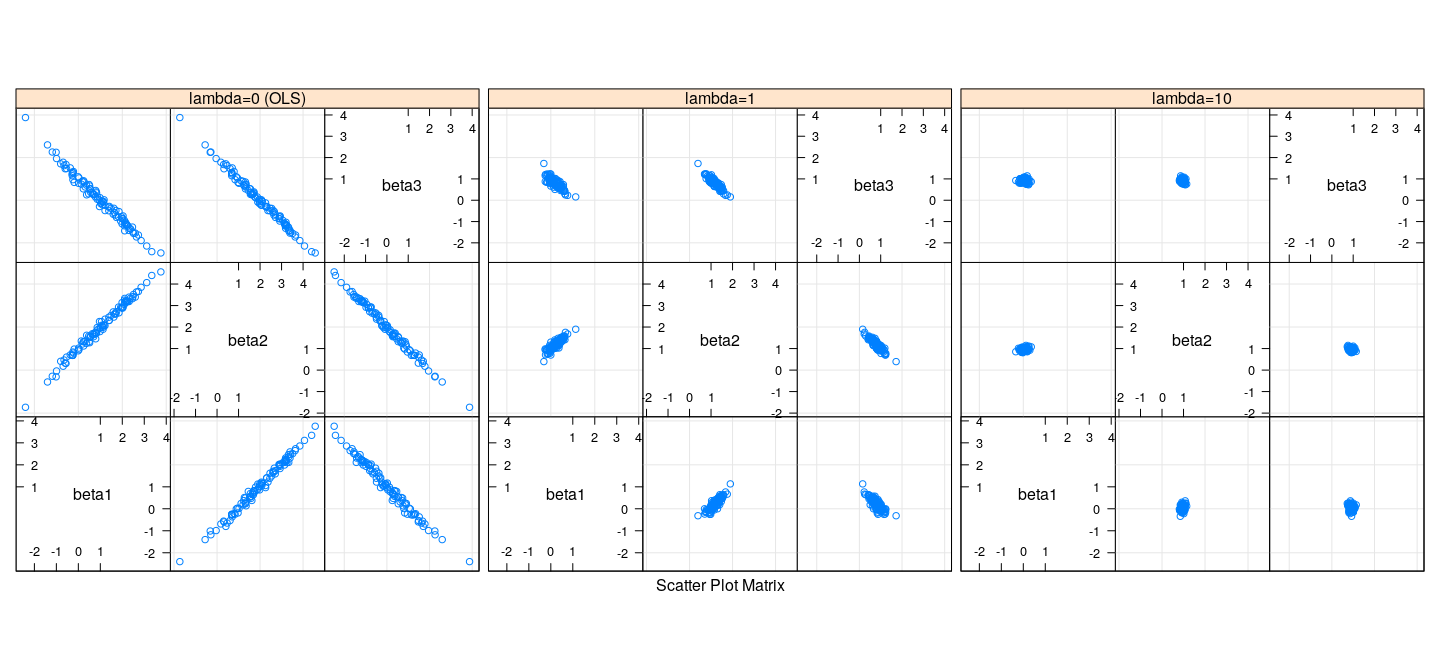
plot of chunk unnamed-chunk-4

Bias and variance of Ridge regression

  • Recall that true \(\beta = (1, 2, 0)\)
     lambda=0 (OLS)  lambda=1  lambda=10
[1,]    1.024926051 0.2217080 0.04698428
[2,]    1.997629453 1.1864466 0.96557666
[3,]   -0.005341892 0.7949516 0.92124664
     lambda=0 (OLS)  lambda=1  lambda=10
[1,]       1.163054 0.2630750 0.11957701
[2,]       1.174441 0.2519598 0.07013490
[3,]       1.171263 0.2512505 0.08062144

Bias and variance of Ridge regression

  • The variance of the ridge estimator is

\[ V(\hat\beta) = \sigma^2 \mathbf{W} \mathbf{X}^T \mathbf{X} \mathbf{W} \quad \text{where} \quad \mathbf{W} = (\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I})^{-1} \]

  • The expectation of the ridge estimator is

\[ E(\hat\beta) = \mathbf{W} \mathbf{X}^T \mathbf{X} \beta \]

  • The bias of the ridge estimator is

\[ \text{bias}(\hat\beta) = (\mathbf{W} \mathbf{X}^T \mathbf{X} - \mathbf{I}) \beta = -\lambda \mathbf{W} \beta \]

  • This follows because

\[ \mathbf{W} (\mathbf{X}^T \mathbf{X} + \lambda \mathbf{I}) = \mathbf{I} \implies \mathbf{W} \mathbf{X}^T \mathbf{X} - \mathbf{I} = \lambda \mathbf{W} \]

Bias and variance of Ridge regression

  • It can be shown that

    • the total variance \(\sum_j V(\hat{\beta}_j)\) is monotone decreasing w.r.t. \(\lambda\)
    • the total squared bias \(\sum_j \text{bias}^2(\hat{\beta}_j)\) is monotone increasing w.r.t. \(\lambda\)

  • It can also be shown that there exists some \(\lambda\) for which the total MSE of \(\hat{\beta}\) is less than the MSE of \(\hat{\beta}_{OLS}\)

  • This is a surprising result that is an instance of a more general phenomenon in decision theory

  • Note however that the total MSE has no useful interpretation for the overall fit

  • We still need to address the problem of choosing \(\lambda\)

  • Before doing so, let us consider a related (but much more interesting) estimator called LASSO

LASSO

  • LASSO stands for “Least Absolute Shrinkage and Selection Operator”

  • The LASSO estimator is given by solving a penalized regression with a \(L_1\) penalty (rather than \(L_2\))

\[ \hat\beta = \arg \min_{\beta} \quad \frac{1}{2} \sum_{i=1}^n (y_i - \mathbf{x}_i^T \beta)^2 + \lambda \sum_{j=1}^p \lvert \beta_j \rvert \]

  • This corresponds to an i.i.d. double exponential prior on each \(\beta_j\)

  • Even though the change seems subtle, the behaviour of the estimator changes dramatically

  • The problem is much more difficult to solve numerically (except when \(\mathbf{X}\) is orthogonal — exercise)

  • It is an area of active research, and implementations have improved considerably over the last few decades

  • We will not go into further theoretical details, but only look at some practical aspects

LASSO in the presence of collinearity

4 x 1 sparse Matrix of class "dgCMatrix"
                    s0
(Intercept) -0.3733872
x1           .        
x2           0.8227224
x3           0.6775433


LASSO in the presence of collinearity

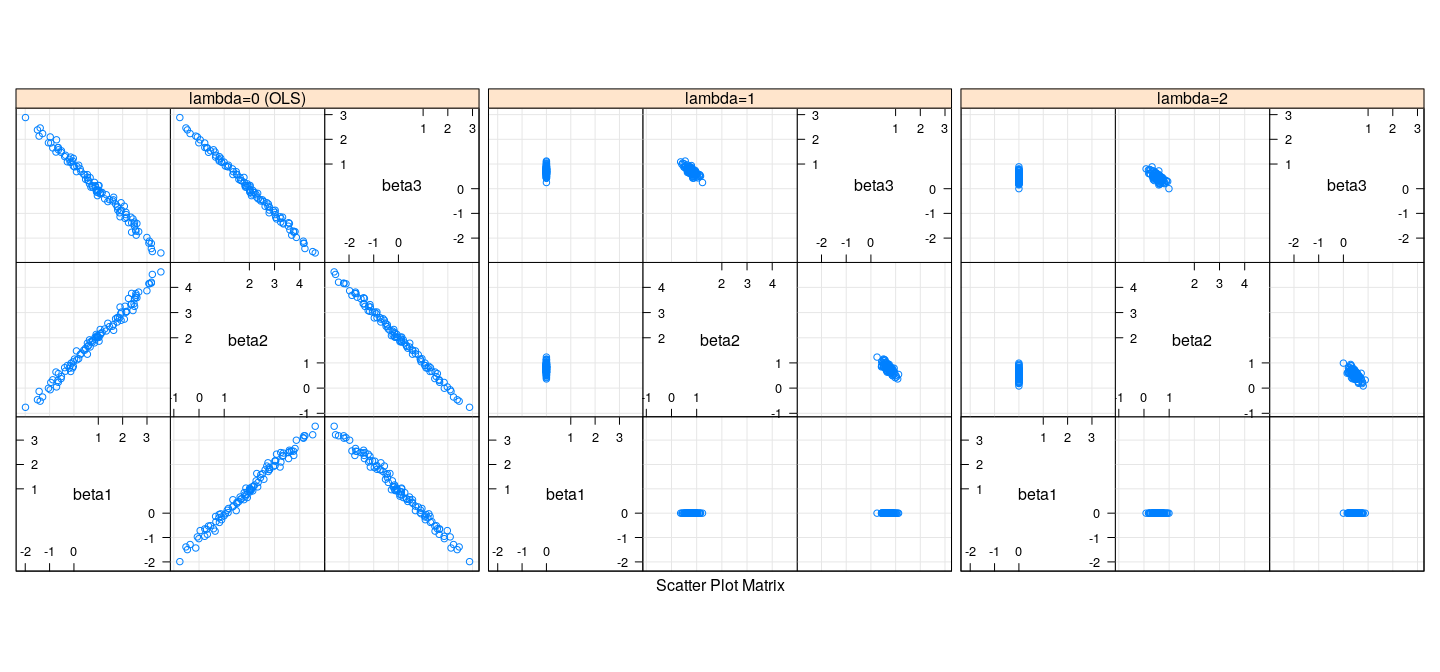
plot of chunk unnamed-chunk-8

LASSO in the presence of collinearity

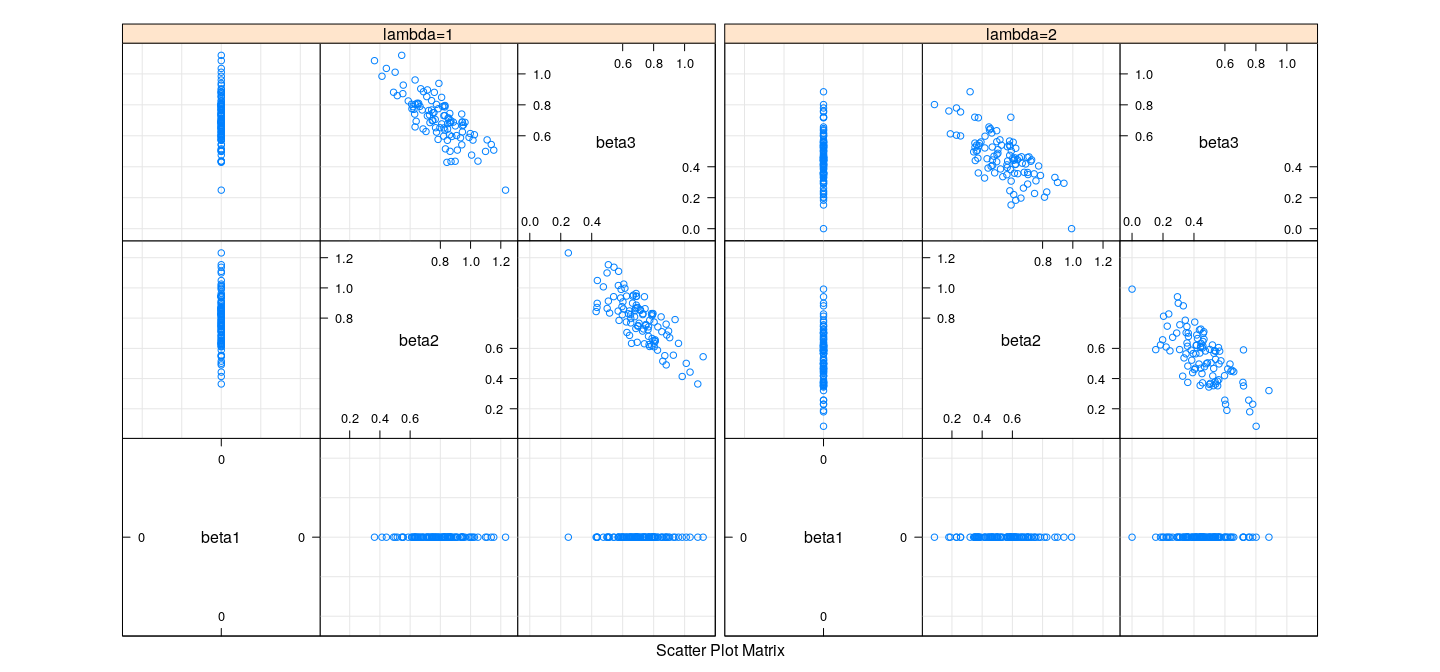
plot of chunk unnamed-chunk-9

Bias and variance of LASSO

  • Recall that true \(\beta = (1, 2, 0)\)
     lambda=0 (OLS)  lambda=1  lambda=2
[1,]    0.972813560 0.0000000 0.0000000
[2,]    2.008541811 0.7920059 0.5423446
[3,]   -0.002656804 0.7109653 0.4587019
     lambda=0 (OLS)  lambda=1  lambda=2
[1,]       1.282199 0.0000000 0.0000000
[2,]       1.274482 0.1630202 0.1698728
[3,]       1.281313 0.1495002 0.1506298

Coefficients as a function of \(\lambda\) : LASSO

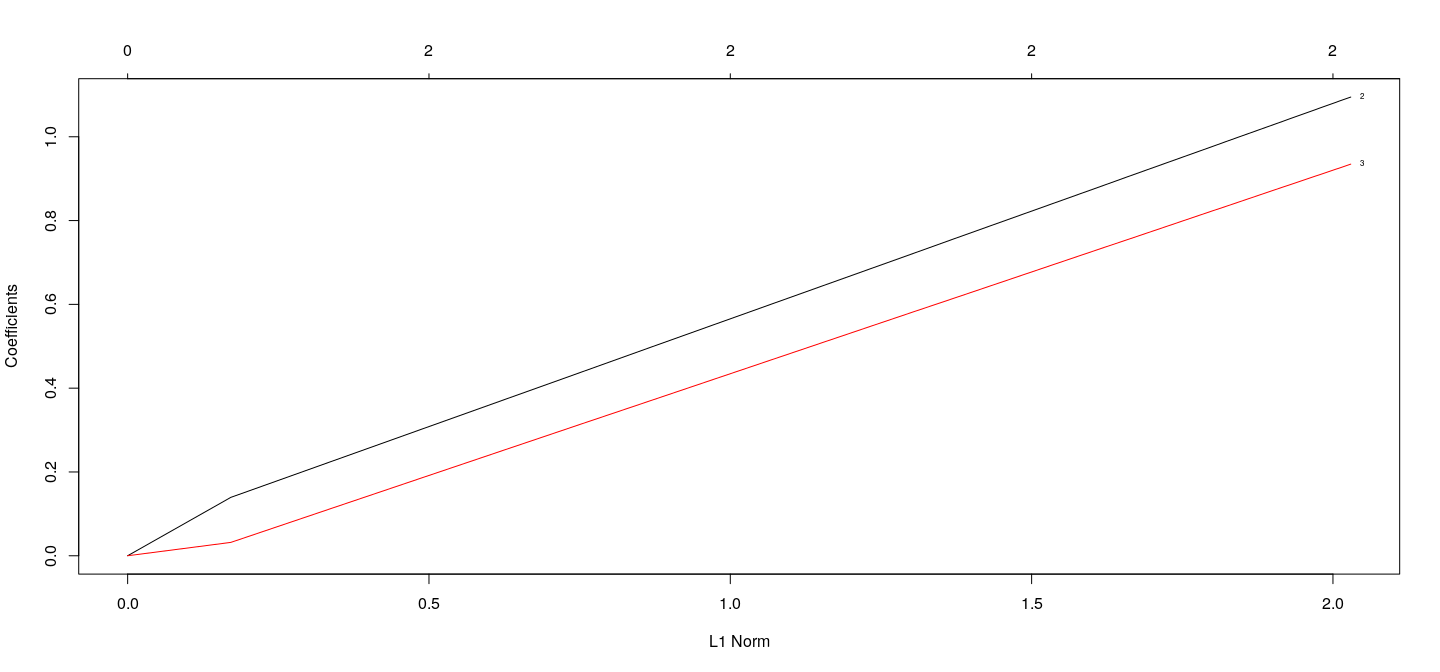
plot of chunk unnamed-chunk-11

Coefficients as a function of \(\lambda\) : LASSO

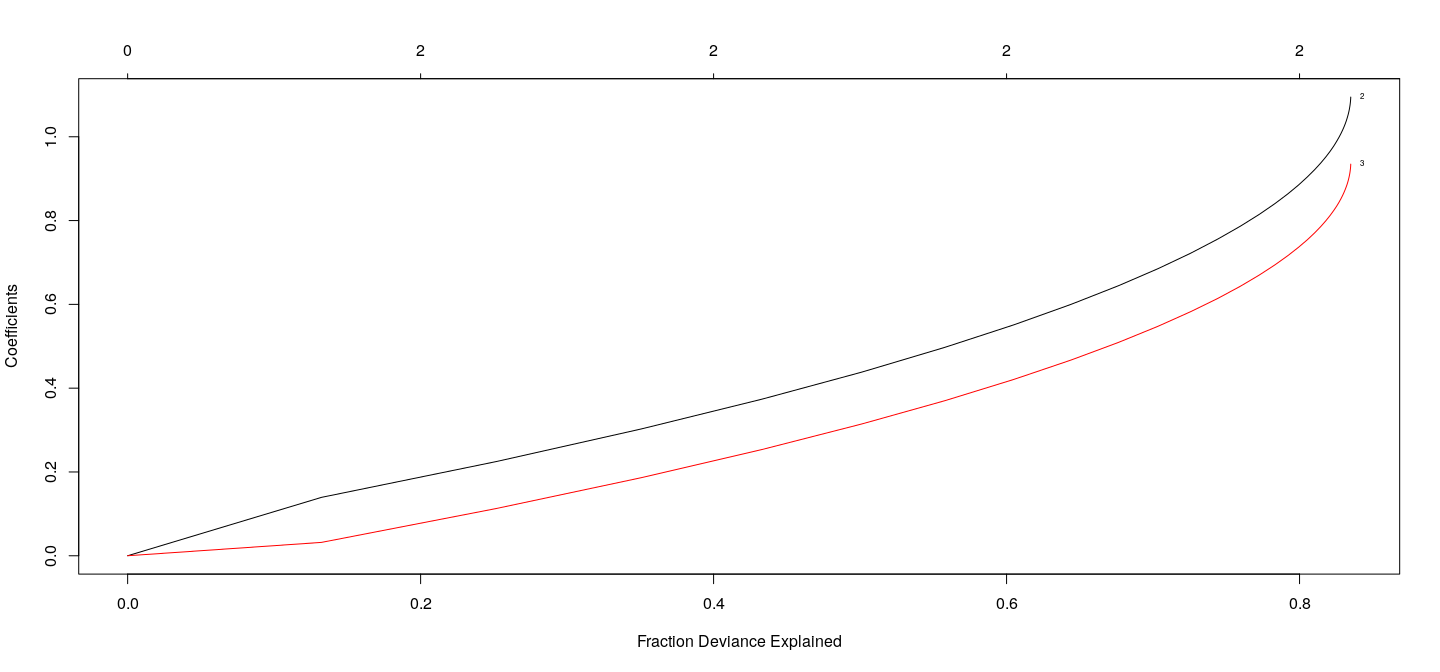
plot of chunk unnamed-chunk-12

Coefficients as a function of \(\lambda\) : Ridge

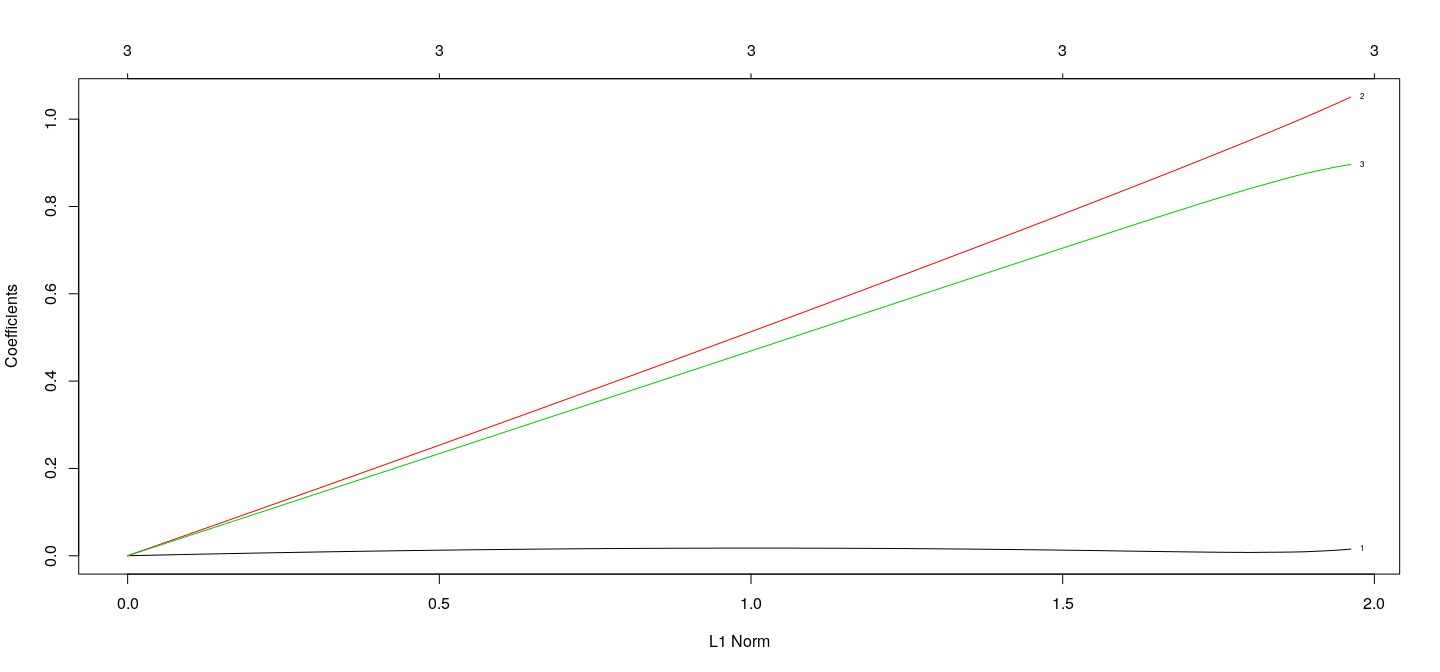
plot of chunk unnamed-chunk-13

Coefficients as a function of \(\lambda\) : Ridge

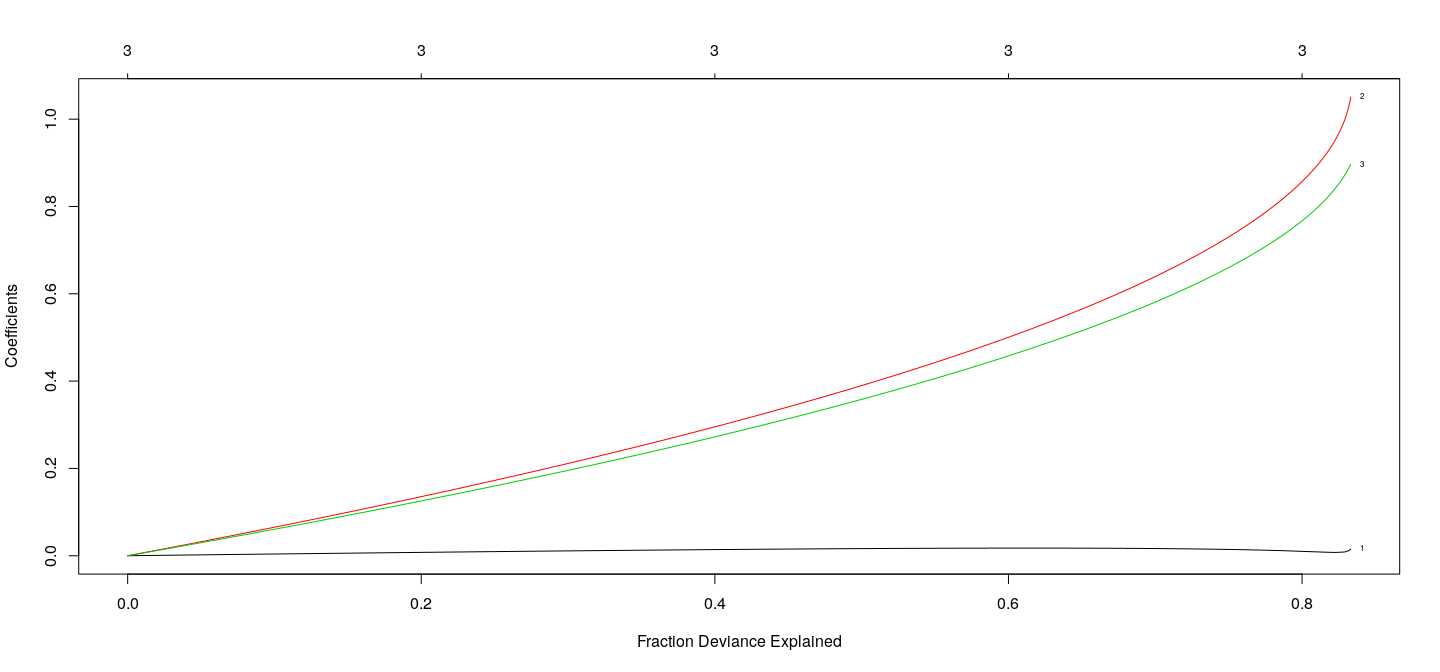
plot of chunk unnamed-chunk-14

Example: Salary of hitters in Major League Baseball (1987)

'data.frame':   322 obs. of  20 variables:
 $ AtBat    : int  293 315 479 496 321 594 185 298 323 401 ...
 $ Hits     : int  66 81 130 141 87 169 37 73 81 92 ...
 $ HmRun    : int  1 7 18 20 10 4 1 0 6 17 ...
 $ Runs     : int  30 24 66 65 39 74 23 24 26 49 ...
 $ RBI      : int  29 38 72 78 42 51 8 24 32 66 ...
 $ Walks    : int  14 39 76 37 30 35 21 7 8 65 ...
 $ Years    : int  1 14 3 11 2 11 2 3 2 13 ...
 $ CAtBat   : int  293 3449 1624 5628 396 4408 214 509 341 5206 ...
 $ CHits    : int  66 835 457 1575 101 1133 42 108 86 1332 ...
 $ CHmRun   : int  1 69 63 225 12 19 1 0 6 253 ...
 $ CRuns    : int  30 321 224 828 48 501 30 41 32 784 ...
 $ CRBI     : int  29 414 266 838 46 336 9 37 34 890 ...
 $ CWalks   : int  14 375 263 354 33 194 24 12 8 866 ...
 $ League   : Factor w/ 2 levels "A","N": 1 2 1 2 2 1 2 1 2 1 ...
 $ Division : Factor w/ 2 levels "E","W": 1 2 2 1 1 2 1 2 2 1 ...
 $ PutOuts  : int  446 632 880 200 805 282 76 121 143 0 ...
 $ Assists  : int  33 43 82 11 40 421 127 283 290 0 ...
 $ Errors   : int  20 10 14 3 4 25 7 9 19 0 ...
 $ Salary   : num  NA 475 480 500 91.5 750 70 100 75 1100 ...
 $ NewLeague: Factor w/ 2 levels "A","N": 1 2 1 2 2 1 1 1 2 1 ...


Example: Salary of hitters in Major League Baseball (1987)

[1] 263  20


Example: Salary of hitters in Major League Baseball (1987)

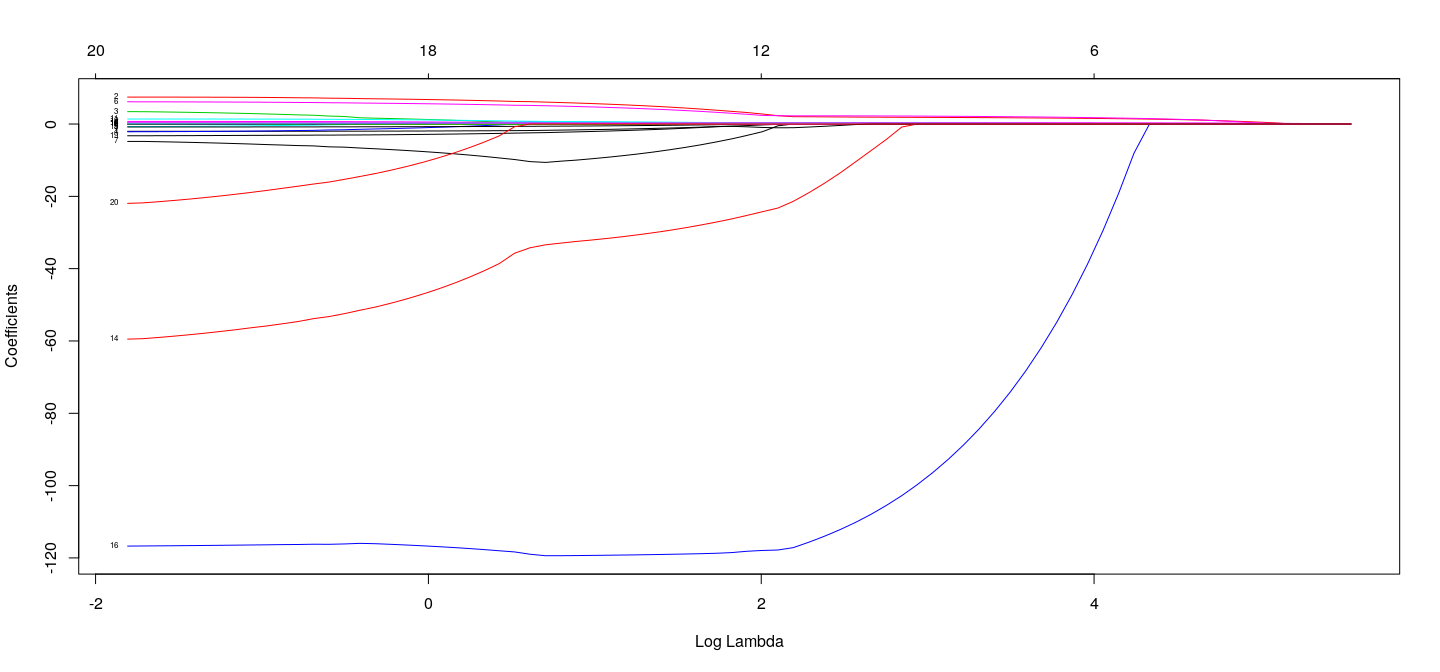
plot of chunk unnamed-chunk-17

Example: Salary of hitters in Major League Baseball (1987)

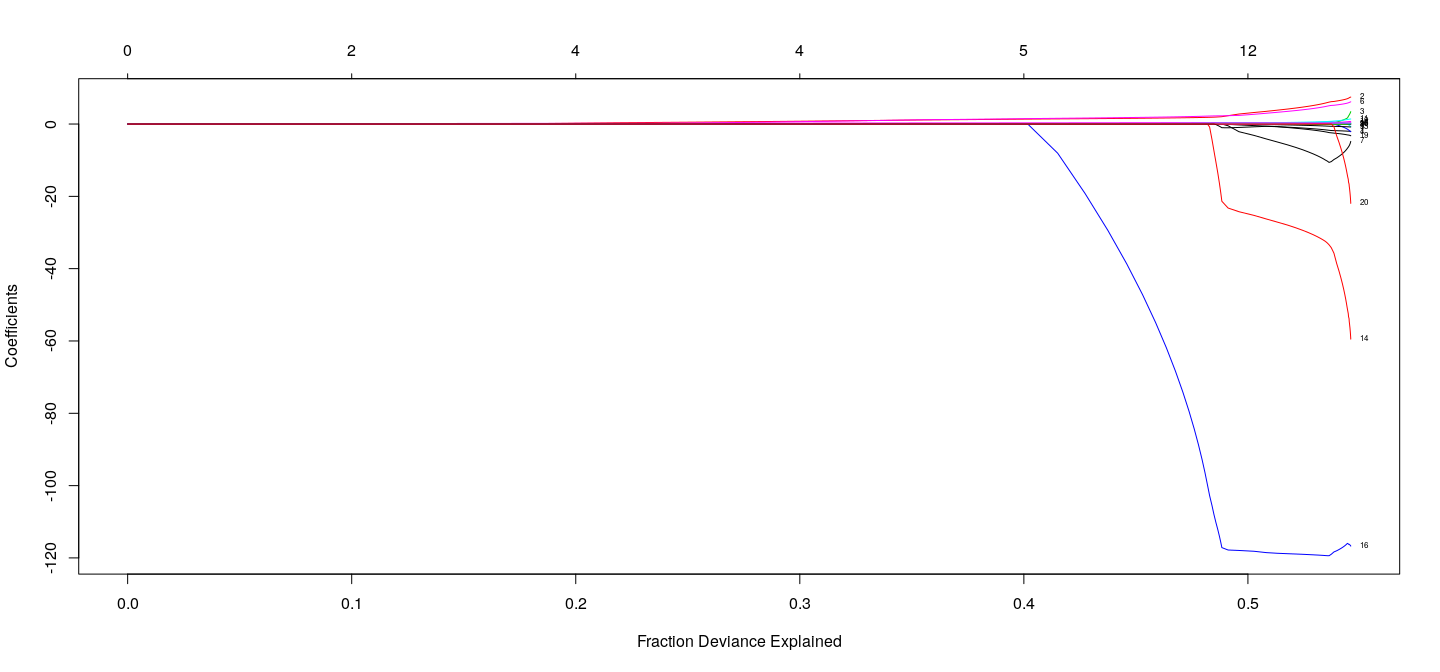
plot of chunk unnamed-chunk-18

Example: Salary of hitters in Major League Baseball (1987)

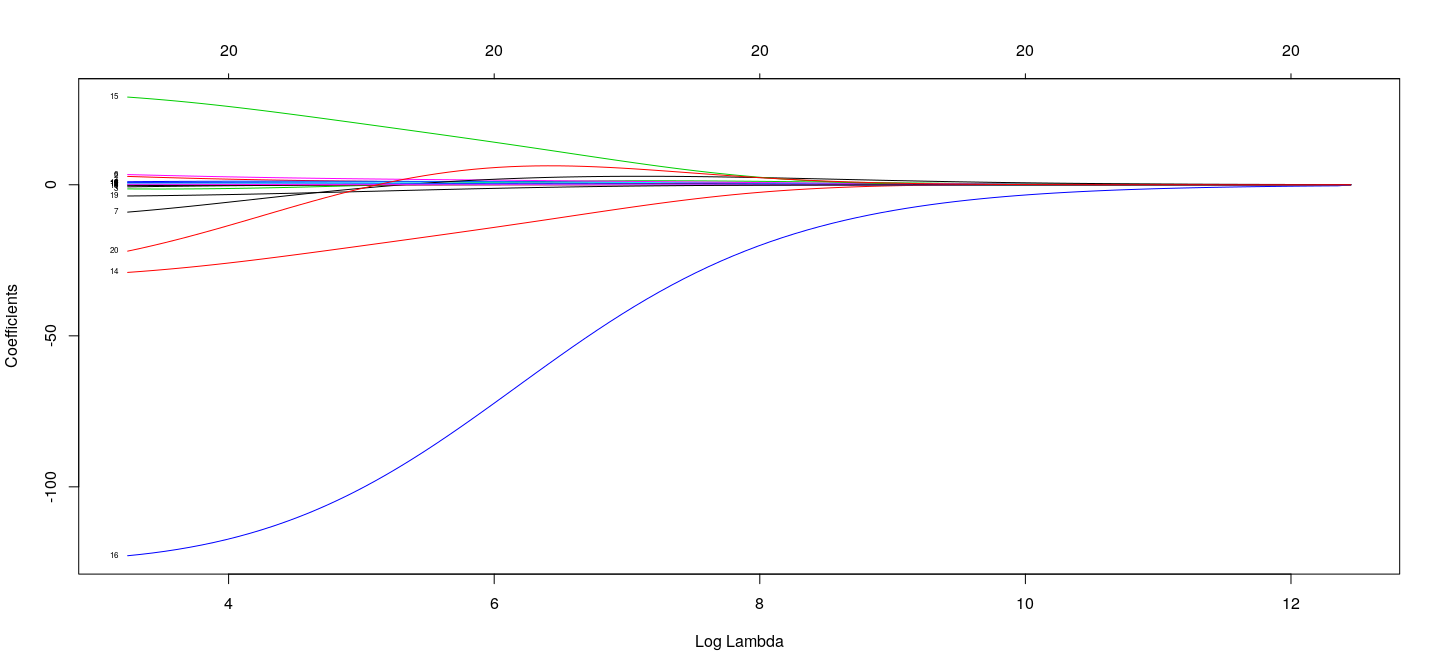
plot of chunk unnamed-chunk-19

Choosing \(\lambda\)

  • Usual model selection criteria can be used (AIC, BIC, etc.)

  • Using cross-validation is more common

  • Note that there is no closed form expression for \(e_{i(-i)}\) in general

  • Leave-one-out (\(n\)-fold) cross-validation is computationally intensive for large data sets

  • The cv.glmnet() function performs \(k\)-fold cross-validation (\(k=10\) by default)

    • Divides dataset randomly into \(k\) (roughly) equal parts

    • Predicts on each part using model fit with remaining \((k-1)\) parts

    • Computes overall prediction error

Choosing \(\lambda\)

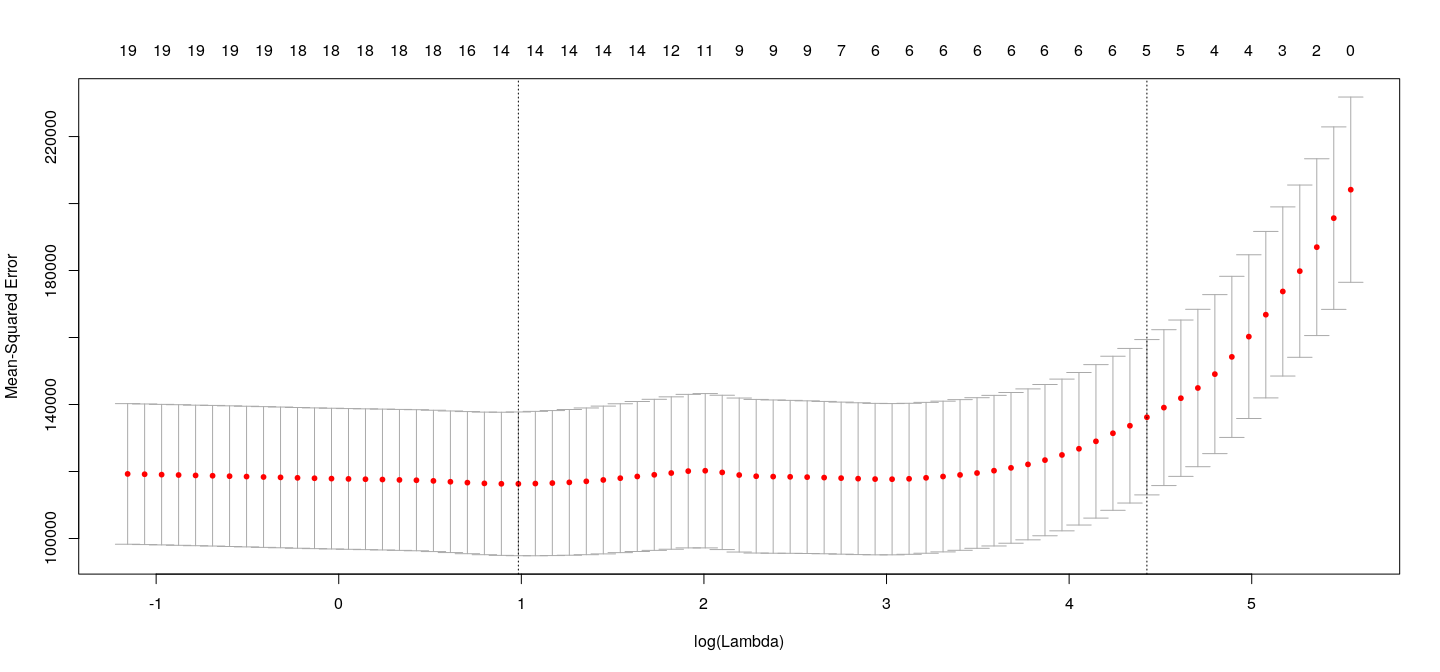
plot of chunk unnamed-chunk-21

Choosing \(\lambda\)

The two lines on the plot correspond to

  • \(\lambda\) that minimizes cross-validation error

  • largest value of \(\lambda\) such that error is within 1 standard error of the minimum

lambda.min lambda.1se 
  2.674375  83.593378

Choosing \(\lambda\)

21 x 2 sparse Matrix of class "dgCMatrix"
                   1       2
(Intercept)  155.817 167.912
AtBat         -1.547   .    
Hits           5.661   1.293
HmRun          .       .    
Runs           .       .    
RBI            .       .    
Walks          4.730   1.398
Years         -9.596   .    
CAtBat         .       .    
CHits          .       .    
CHmRun         0.511   .    
CRuns          0.659   0.142
CRBI           0.393   0.322
CWalks        -0.529   .    
LeagueA      -32.065   .    
LeagueN        0.000   .    
DivisionW   -119.299   .    
PutOuts        0.272   0.047
Assists        0.173   .    
Errors        -2.059   .    
NewLeagueN     .       .

Choosing \(\lambda\)

plot of chunk unnamed-chunk-24

How well does LASSO work for variable selection?

num.nonzero.coefs
 0  2 
99  1


  • So Type-I error probability is much lower for LASSO compared to stepwise regression

How well does LASSO work for variable selection?

  • How about power to detect effects that are present? Choose \(\beta_1, \beta_2 \sim U(-1, 1)\), other \(\beta_j = 0\)

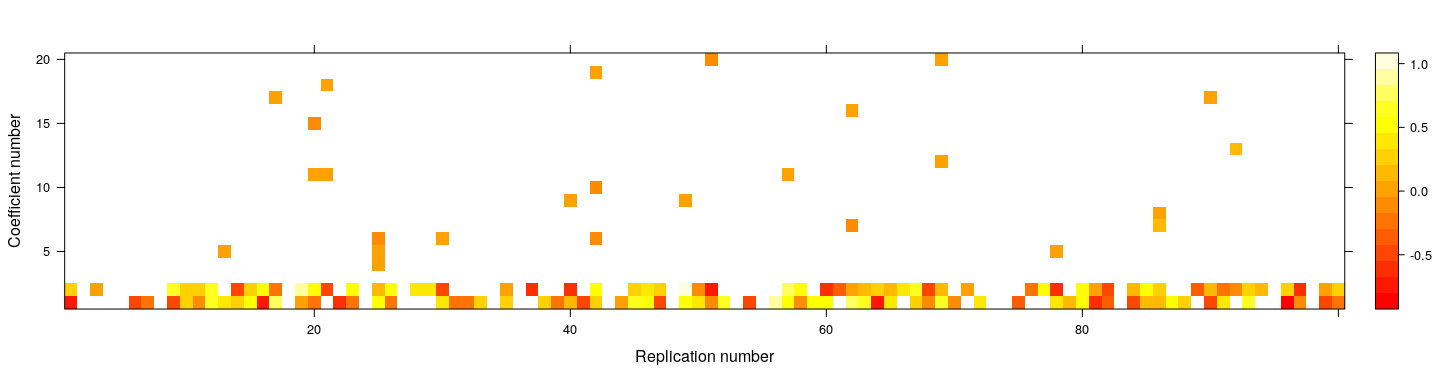
plot of chunk unnamed-chunk-26

Why does LASSO lead to exact 0 coefficients?

  • Alternative formulation of Ridge regression: consider problem of minimizing

\[ \sum_{i=1}^n (y_i - \mathbf{x}_i^T \beta)^2 \quad \text{subject to} \quad \lVert \beta \rVert^2 = \sum \beta_j^2 \leq t \]

  • Claim: The solution \(\hat{\beta}\) is the usual Ridge estimate for some \(\lambda\)

  • Case 1 : \(\lVert \hat{\beta}_{OLS} \rVert^2 \leq t \implies \hat{\beta} = \hat{\beta}_{OLS}, \lambda = 0\)

  • Case 2 : \(\lVert \hat{\beta}_{OLS} \rVert^2 > t\)

    • Then must have \(\lVert \hat{\beta} \rVert^2 = t\) (otherwise can move closer to \(\hat{\beta}_{OLS}\))
    • The Lagrangian is \(\lVert \mathbf{y} - \mathbf{X} \beta \rVert^2 + \lambda \lVert \hat{\beta} \rVert^2 - \lambda t\)
    • This is the same optimization problem as before
    • \(\lambda\) is defined implicitly as a function of \(t\), to ensure \(\lVert \hat{\beta} \rVert^2 = t\)

  • The LASSO problem can be similarly formulated as: minimize \(\lVert \mathbf{y} - \mathbf{X} \beta \rVert^2\) subject to \(\sum \lvert \beta_j \rvert \leq t\)

  • This interpretation gives a useful geometric justification for the variable selection behaviour of LASSO

Comparative geometry of Ridge and LASSO optimization

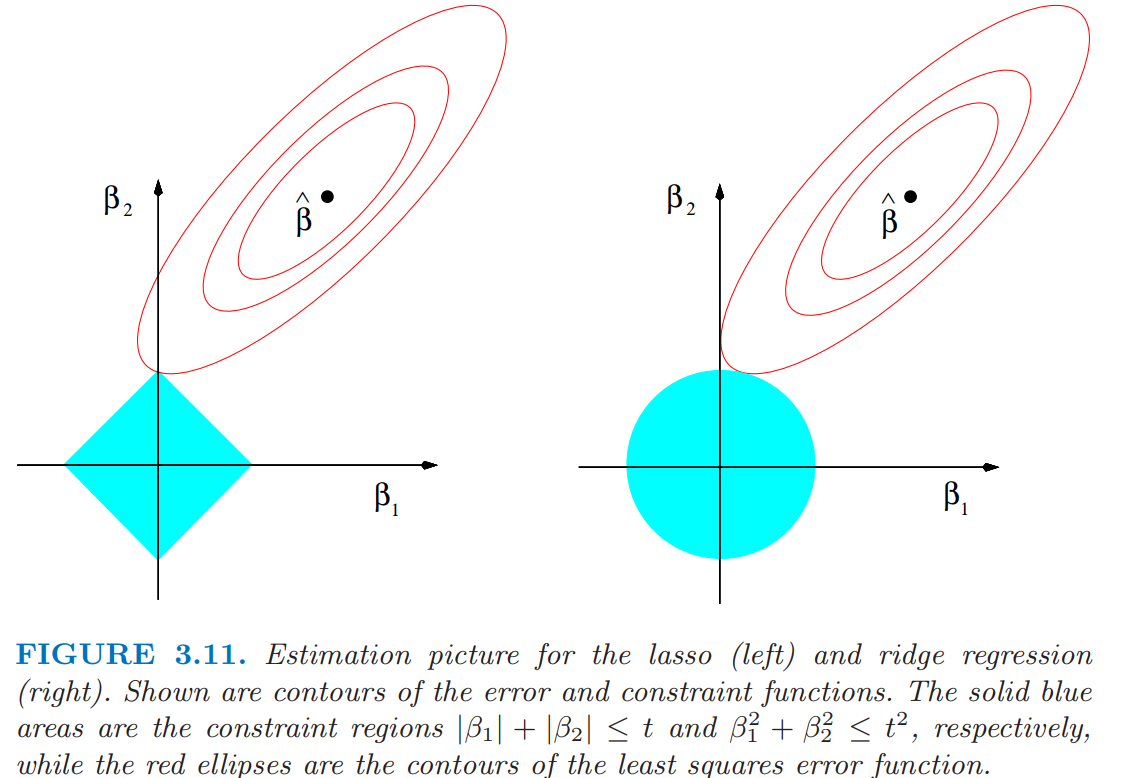
(From Elements of Statistical Learning, page 71)