Diagnosing Systematic Model Violations
Deepayan Sarkar
Violation of assumptions in a linear regression model
Systematic violations
- Non-normality of errors
- Nonconstant error variance
- Lack of fit (nonlinearity)
- (Autocorrelation in errors — later)
Non-normality of errors
- Why do we care? LSE is Best Linear Unbiased Estimator under assumptions of
- linearity
- constant variance
- uncorrelated errors
Even if LSE is valid, it may not be efficient, especially with heavy tailed errors (outliers)
LSE estimates conditional mean \(f(x) = E(Y | X = x)\)
Justified when distribution of \(Y | X = x\) is symmetric
May not be appropriate measure of central tendency if distribution of \(Y | X = x\) is skewed
Multimodal error distribution usually indicates presense of latent covariate
Graphical techniques
Although formal tests exist, we will focus on graphical techniques
More useful in practice because they can pinpoint nature of violation
SLID <- na.omit(SLID[-5])
fm <- lm(wages ~ education + age + sex, data = SLID) # no interaction for now
e <- rstudent(fm) # should have t-distribution (not independent)
plot(density(e, bw = 0.1))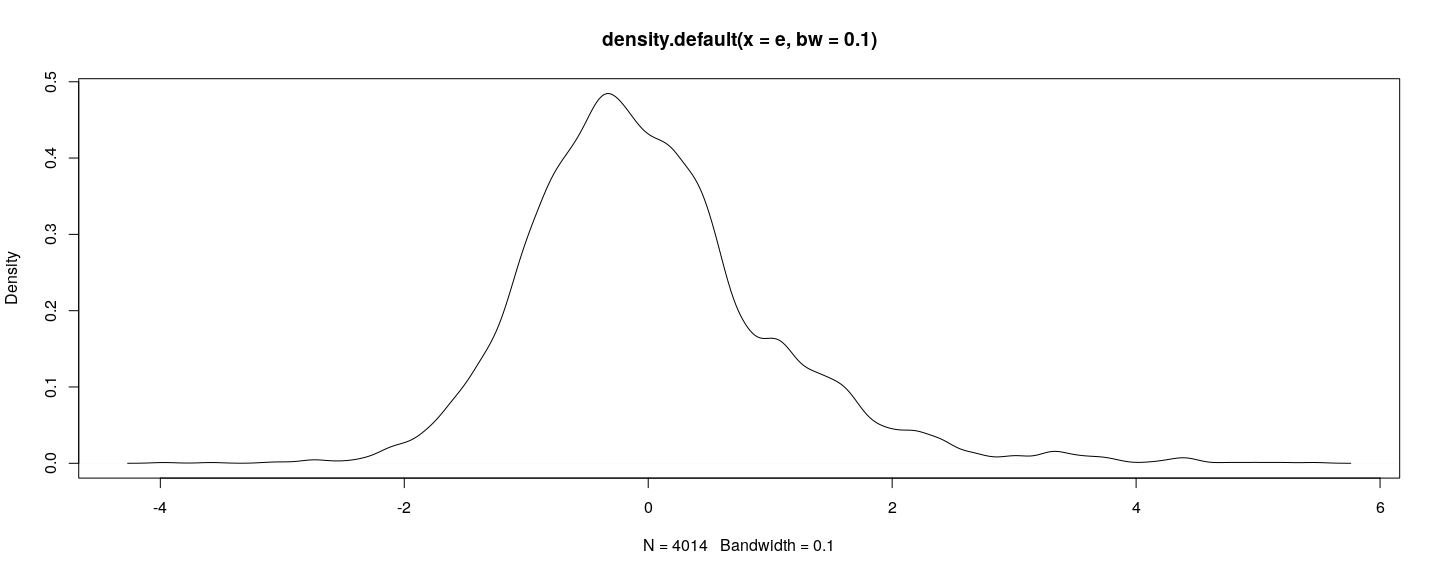
Graphical techniques
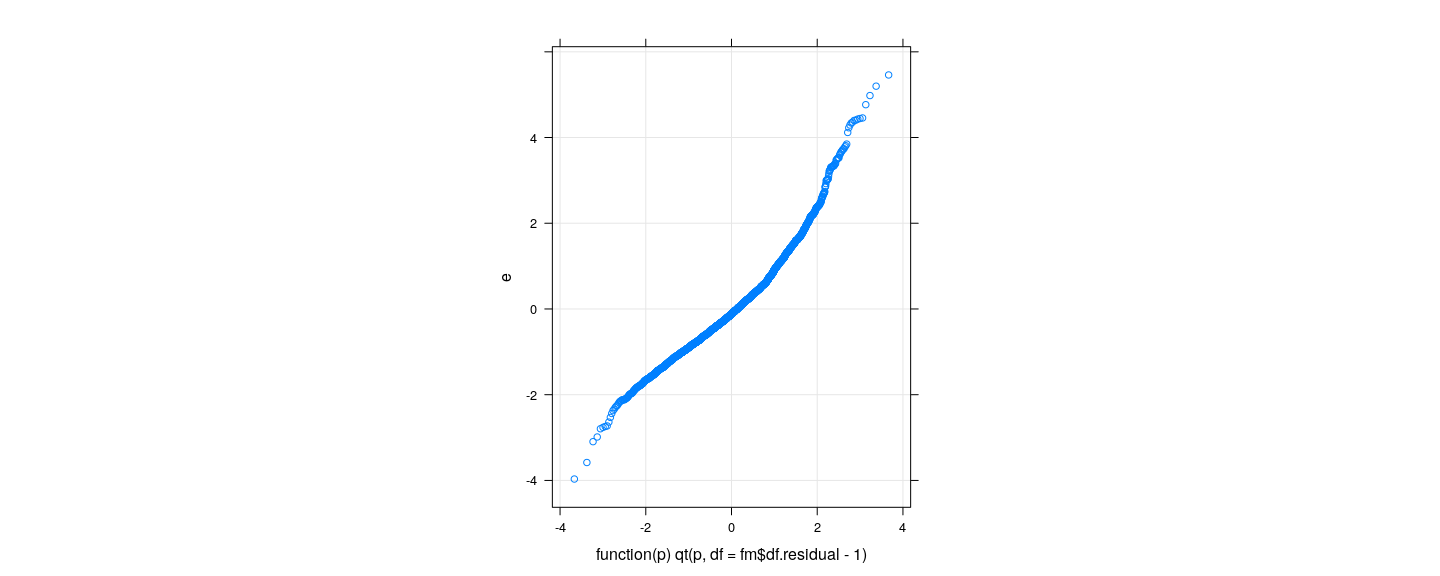
- But is there a reference to compare to?
Confidence bounds for QQ-plots using Parametric Bootstrap
Dependence structure in Studentized residuals can be replicated using simulation:
- simulate \(\mathbf{y} \sim N(\mathbf{X} \hat{\beta},\hat{\sigma}^2 \mathbf{I})\)
- calculate Studentized residuals for simulated response
- provides replicates from null distribution (free of \(\beta\) and \(\sigma^2\))
Empirical (simulation) distribution of \(i\)-th order statistic gives pointwise interval
yhat <- fitted(fm)
sigma.hat <- summary(fm)$sigma
n <- length(yhat)
sime <- function()
{
SLID$ysim <- rnorm(n, mean = yhat, sd = sigma.hat)
sort(rstudent(lm(ysim ~ education + age + sex, data = SLID)))
}
esim <- replicate(5000, sime())
qsim <- apply(esim, 1, quantile, probs = c(0.005, 0.995)) # 99% pointwiseConfidence bounds for QQ-plots using Parametric Bootstrap
xyplot(sort(rstudent(fm)) ~ qt(ppoints(n), df = fm$df.residual - 1), grid = TRUE, aspect = "iso") +
layer_(panel.polygon(c(x, rev(x)), c(qsim[1,], rev(qsim[2,])), col = "grey", border = NA))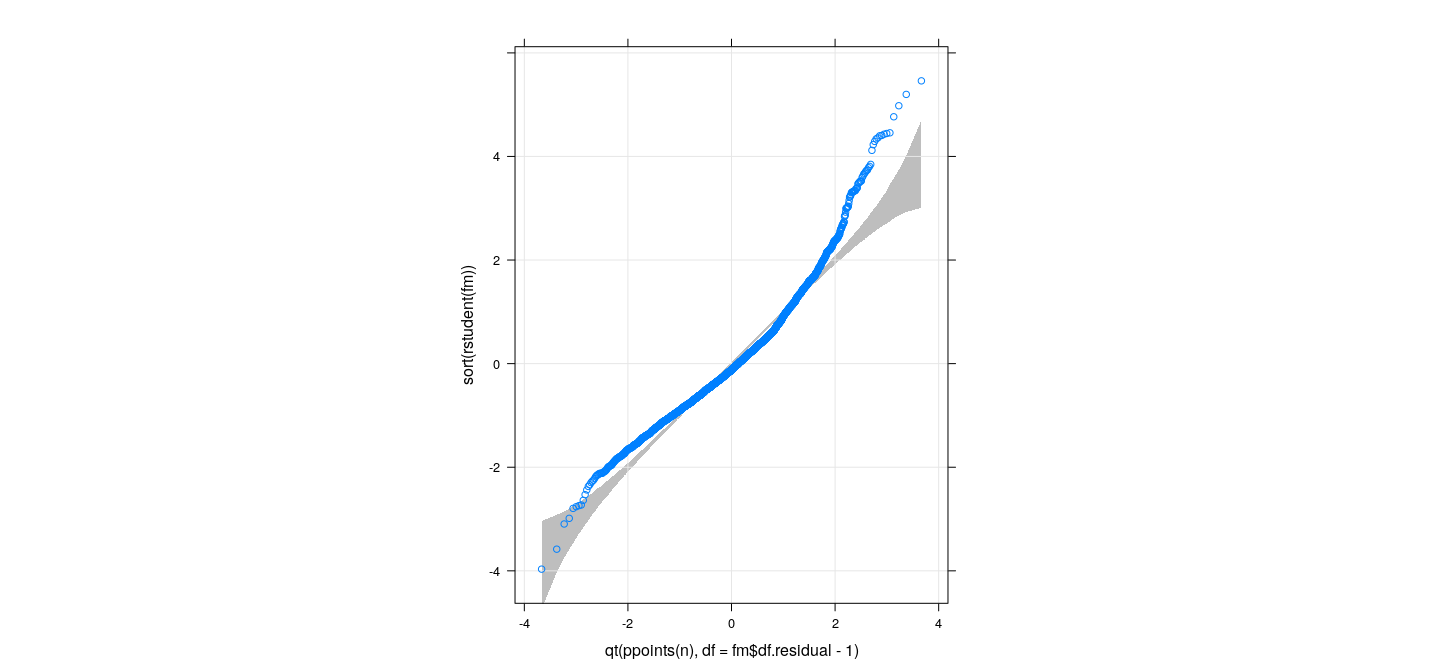
How can we address non-Normality?
Sometimes, a more general model may be appropriate (e.g., GLMs, to be studied later)
Often, transforming the response can prove useful
- E.g., variance stabilizing transformations (depending on distributions)
- \(\sqrt{y}\) for Poisson
- \(\sin^{-1} (\sqrt{y})\) for Binomial
\(\log y\) for positive-valued data (especially economic data)
Logit transform \(\log (p / (1-p))\) for proportions
Power transformations
Generally useful family: power transformations
Box-Cox family (remains increasing for negative powers, incorporates \(\log\) as limit)
\[ g_\lambda(y) = \begin{cases} \frac{y^\lambda - 1}{\lambda} & \lambda \neq 0 \\ \log y & \lambda = 0 \end{cases} \]
Power transformations
bc <- function(x, lambda) { if (lambda == 0) log(x) else (x^lambda - 1) / lambda }
y <- rlnorm(500)
densityplot(~ y + bc(y, 1/3) + bc(y, 1/2) + bc(y, 0) + bc(y, -1/2) + bc(y, -1),
plot.points = FALSE, outer = TRUE, xlab = NULL, scales = list(x = "free"))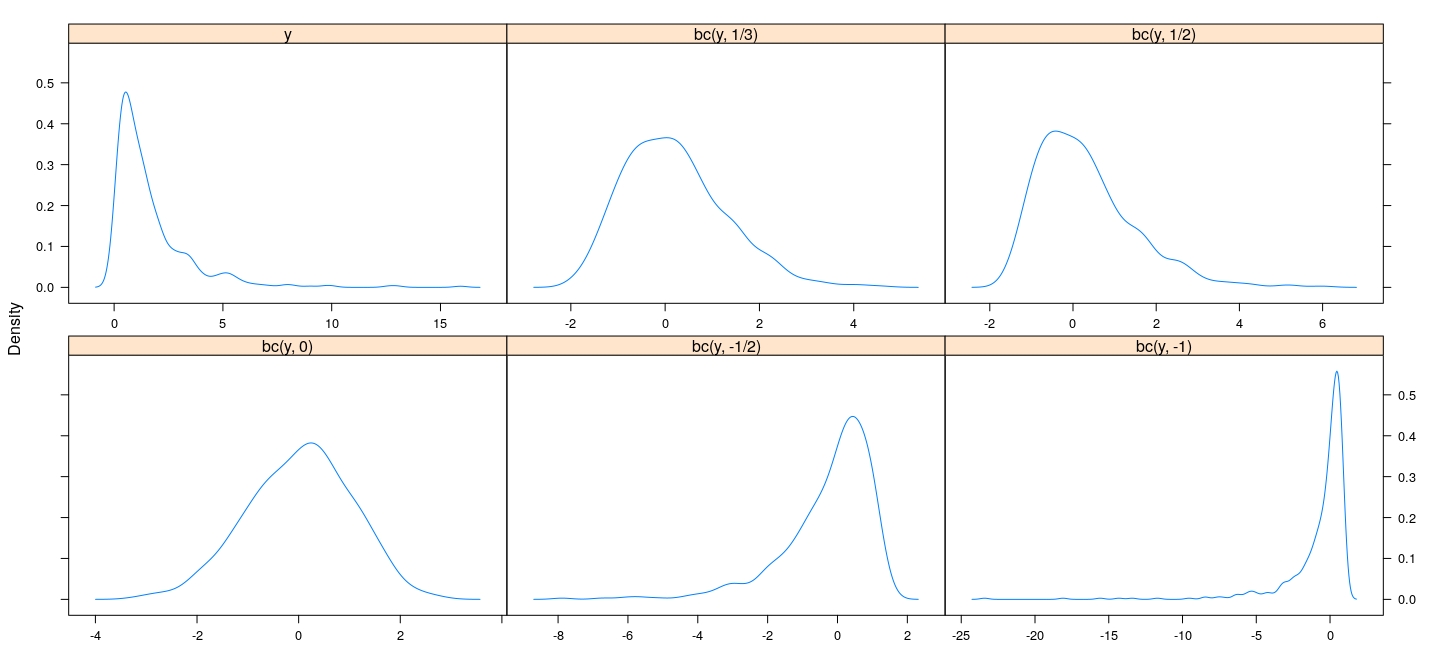
Power transformations
x <- runif(500, -3, 3)
y <- rlnorm(500, mean = x, sd = 1)
xyplot(y + bc(y, 1/3) + bc(y, 1/2) + bc(y, 0) + bc(y, -1/2) + bc(y, -1) ~ x,
plot.points = FALSE, outer = TRUE, xlab = NULL, scales = list(y = "free"))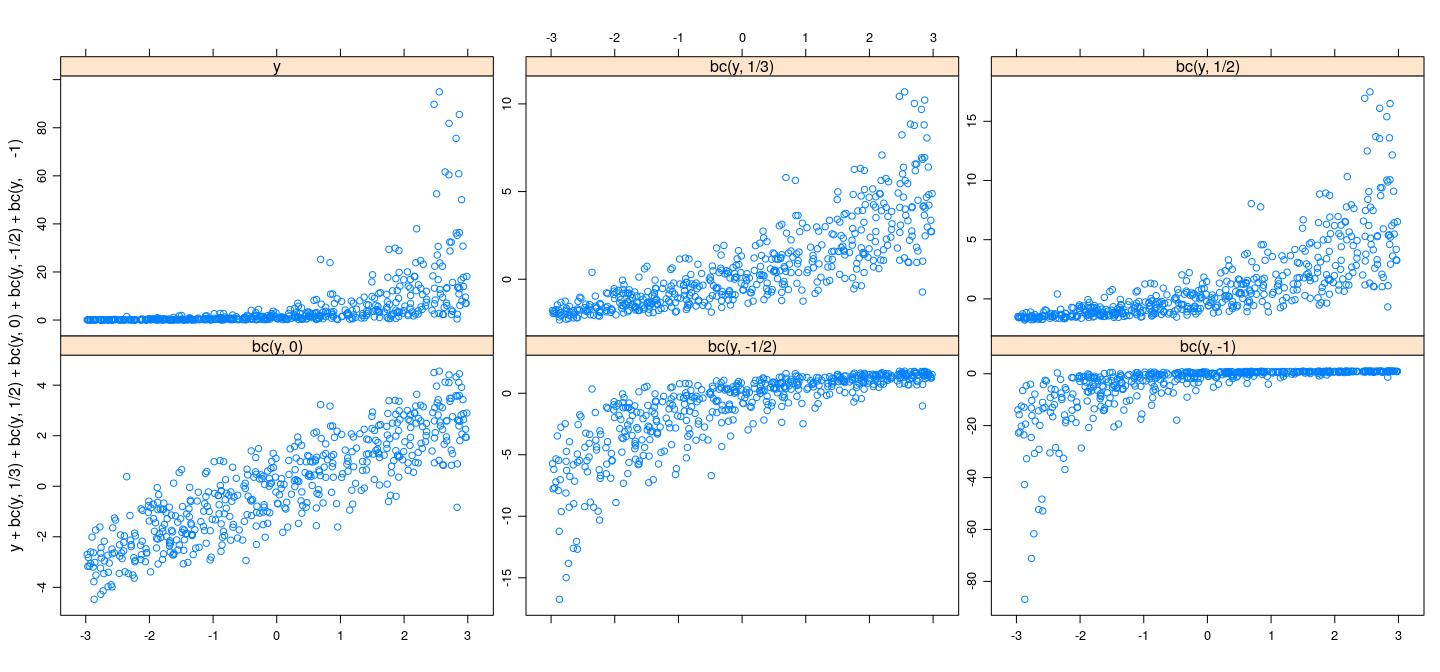
Power transformations
Generally useful family: power transformations
Box-Cox family (remains increasing for negative powers, incorporates \(\log\) as limit)
\[ g_\lambda(y) = \begin{cases} \frac{y^\lambda - 1}{\lambda} & \lambda \neq 0 \\ \log y & \lambda = 0 \end{cases} \]
\(\lambda\) can be “estimated” using a formal approach (will discuss later)
More common to guess based on context
In this case, error distribution is right-skewed, so could try \(\log\), square root, cube root, etc.
- Important to note that (non-linear) transformations affect many aspects together:
- Distribution of errors
- Linearity
- Nonconstant error variance
Modeling transformed data
e.2 <- rstudent(fm.2 <- lm(bc(wages, 1/2) ~ education + age + sex, data = SLID))
e.3 <- rstudent(fm.3 <- lm(bc(wages, 1/3) ~ education + age + sex, data = SLID))
e.log <- rstudent(fm.log <- lm(log(wages) ~ education + age + sex, data = SLID))
densityplot(~ e + e.2 + e.3 + e.log, bw = 0.1, plot.points = FALSE, outer = TRUE,
xlab = NULL, scales = list(x = "free"))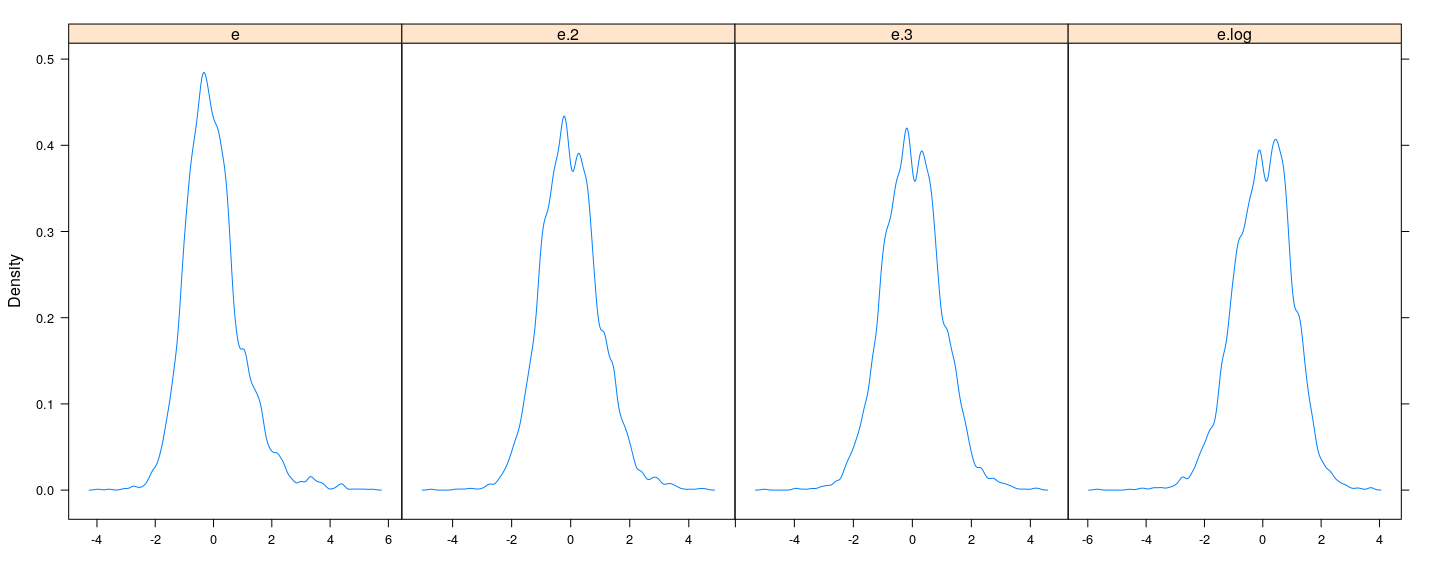
Modeling transformed data
xyplot(sort(rstudent(fm)) + sort(rstudent(fm.2)) + sort(rstudent(fm.3)) +
sort(rstudent(fm.log)) ~ qt(ppoints(n), df = fm$df.residual - 1),
outer = TRUE, grid = TRUE, aspect = "iso", ylab = "Studentized residuals") +
layer_(panel.polygon(c(x, rev(x)), c(qsim[1,], rev(qsim[2,])), col = "grey", border = NA))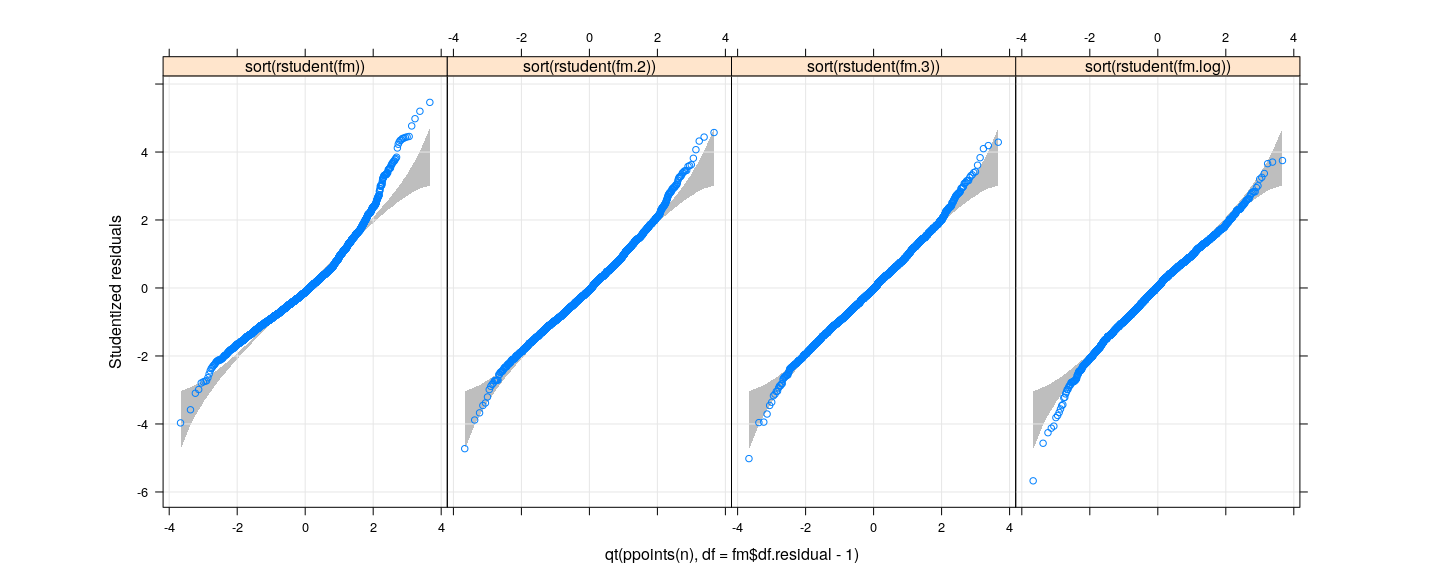
The same confidence bounds work for all cases! (exercise)
Formal tests: Kolmogorov-Smirnoff
One-sample Kolmogorov-Smirnov test
data: e
D = 0.063411, p-value = 1.91e-14
alternative hypothesis: two-sided
One-sample Kolmogorov-Smirnov test
data: e.log
D = 0.025792, p-value = 0.009588
alternative hypothesis: two-sided
One-sample Kolmogorov-Smirnov test
data: e.3
D = 0.015434, p-value = 0.2946
alternative hypothesis: two-sidedFormal tests: Shapiro-Wilk test
Shapiro-Wilk normality test
data: e
W = 0.95974, p-value < 2.2e-16
Shapiro-Wilk normality test
data: e.log
W = 0.99431, p-value = 1.844e-11
Shapiro-Wilk normality test
data: e.3
W = 0.99662, p-value = 7.311e-08More details: Kolmogorov-Smirnoff test
Null hypothesis: \(X_1, \dotsc, X_n \sim \text{ i.i.d. } F_0\) (where \(F_0\) is a completely specified absolutely continuous CDF)
Empirical CDF
\[\hat{F}_n(x) = \frac{1}{n} \sum_i \mathbf{1} \{ X_i \leq x \}\]
- Test statistic:
\[T(X_1, \dotsc, X_n) = \sup_{x \in \mathbb{R}} \lvert \hat{F}_n(x) - F_0(x) \rvert\]
- Note that
- null distribution of \(T\) does not depend on \(F_0\) (use \(U_i = F_0(X_i) \sim \text{ i.i.d. } U(0, 1)\) instead)
- Intuitively, large value of \(T\) indicates departure from null, so reject when \(T\) is large
- \(p\)-value can be approximated using simulation
- Can also be estimated conservatively using the DKW inequality
More details: Shapiro-Wilk test
Null hypothesis: \(X_1, \dotsc, X_n \sim \text{ i.i.d. } N(\mu, \sigma^2)\) for some \(\mu, \sigma^2\)
Test statistic
\[W = \frac{ (\sum_i a_i X_{(i)})^2 }{\sum_i (X_i - \bar{X})^2}\]
- where
\[\mathbf{a} = \frac{\mathbf{m}^T \mathbf{V}}{\sqrt{\mathbf{m}^T \mathbf{V}^{-1} \mathbf{V}^{-1} \mathbf{m}} }\]
with \(\mathbf{m}\) and \(\mathbf{V}\) the mean vector and variance-covariance matrix of \((Z_{(1)}, \dotsc, Z_{(n)})^T\), where \(Z_1, \dotsc, Z_n \sim \text{ i.i.d. } N(0, 1)\)
The motivation (and implementation) for this test is slightly complicated, but the basic idea is that \(\sum_i a_i X_{(i)}\) estimates the slope of the Normal Q-Q plot (which is an estimate of \(\sigma\)). See Shapiro and Wilk, 1965 for details.
Summary
log, square root, cube root all reasonable (graphically)
Formal tests are sometimes too sensitive (especially for large data)
Formal tests useful, but should not be taken too seriously
Nonconstant error variance
No obvious way to detect unless there is a systematic pattern
Typical patterns:
\(V(Y | X = x)\) depends on \(E(Y | X = x)\)
\(V(Y | X = x)\) depends on \(x\)
Graphical methods: plot residuals against fitted values / covariates
Plotting Residuals vs fitted values
Residuals (\(\mathbf{y} - \hat{\mathbf{y}}\)) are uncorrelated with fitted values (\(\hat{\mathbf{y}}\)) (but not with \(\mathbf{y}\))
Residuals have unequal variances, so preferable to plot Studentized residuals
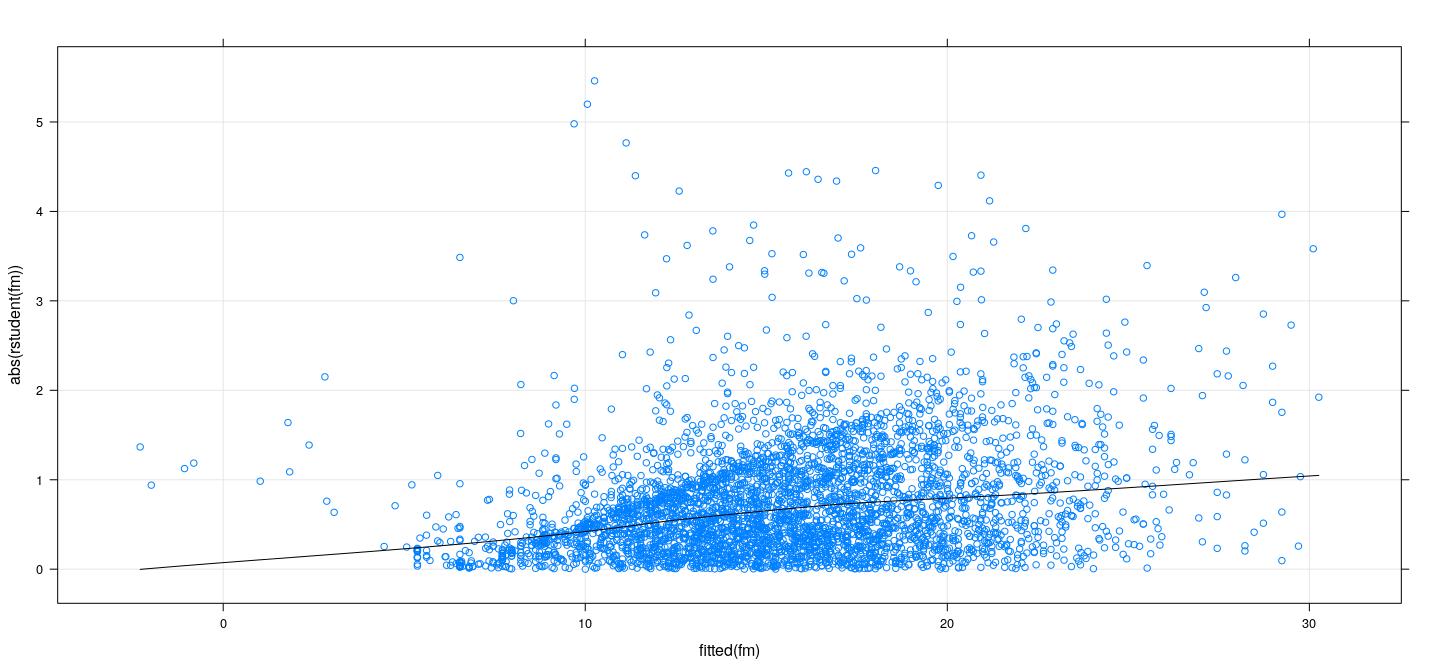
If true error variances depend on \(E(Y | X = x)\), we expect to see the same dependence in plot
More useful to plot absolute Studentized residuals (\(\lvert t_i \rvert\)) along with a non-parametric smoother
Studentized residuals vs fitted values
fm <- lm(wages ~ education + age + sex, data = SLID)
xyplot(rstudent(fm) ~ fitted(fm), type = c("p", "smooth"), grid = TRUE,
col.line = "black", abline = list(h = 0, col = "grey50"))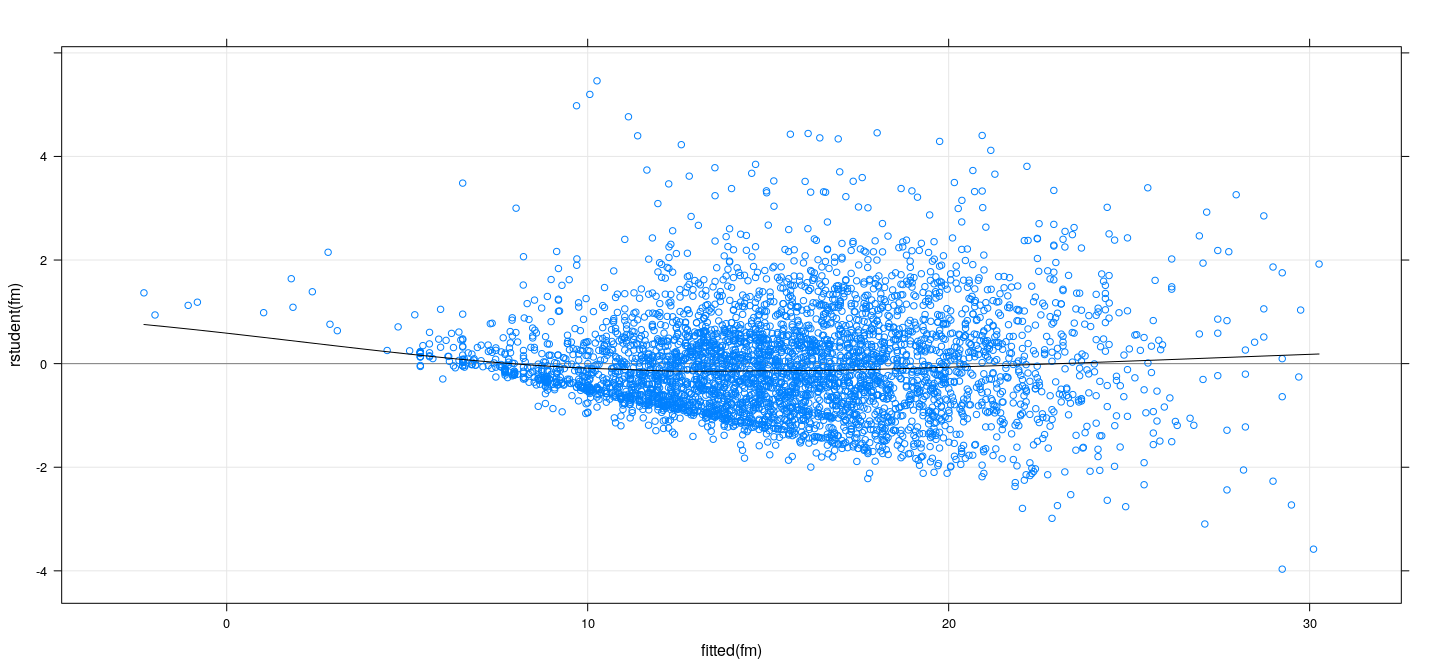
Absolute Studentized residuals vs fitted values
Spread-level plots
Suppose (most) fitted values are positive
We can plot both absolute residuals and fitted values in log scales
A linear relationship in this plot suggests a power transformation
Spread-level plots
xyplot(abs(rstudent(fm)) ~ fitted(fm), type = c("p", "r", "smooth"), grid = TRUE,
col.line = "black", scales = list(log = TRUE, equispaced.log = FALSE))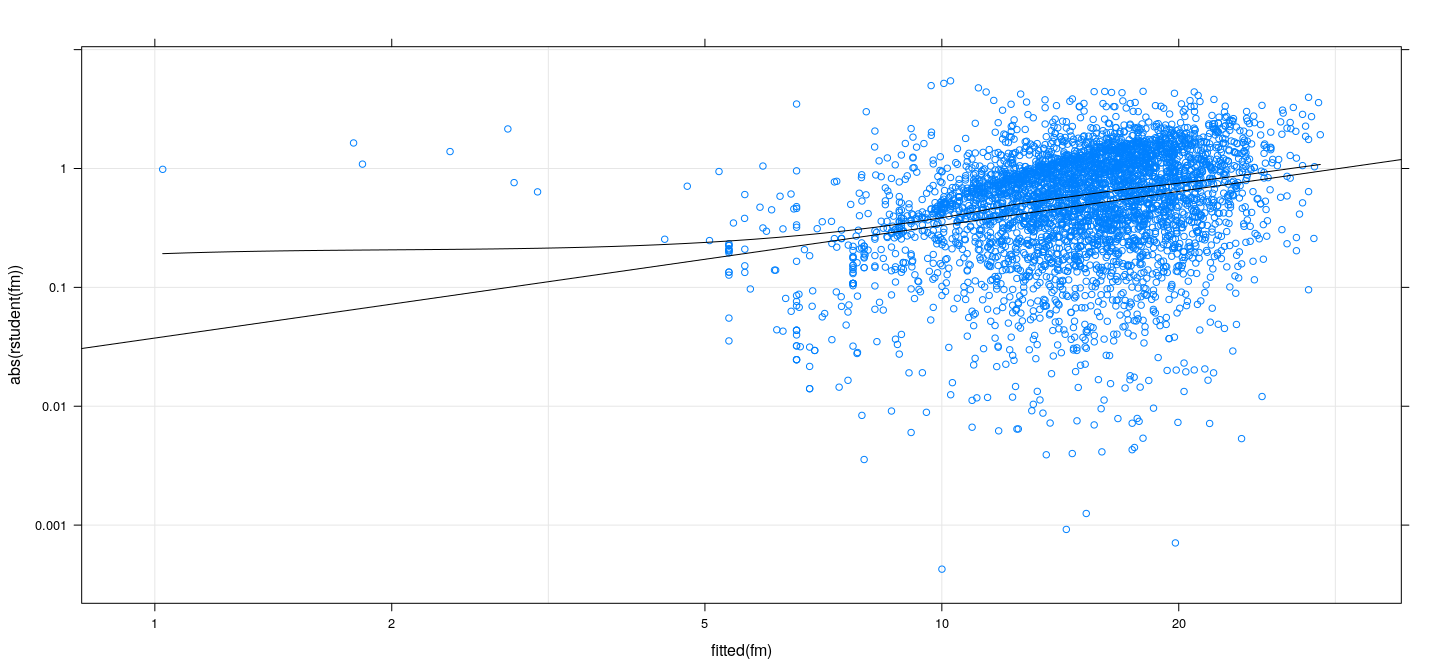
Spread-level plots and power transformations
Let \(\mu = E(Y)\) and suppose \(V(Y) = h(\mu) = (a \mu^b)^2\)
What is the variance stabilizing transformation?
Empirical rule: \(g(Y)\) has approximately constant variance where
\[ g(y) = \int \frac{C}{\sqrt{h(y)}} dy = C \int y^{-b} dy = C y^{1-b} \]
Spread-level plots and power transformations
On the other hand, errors \(\varepsilon = Y - \mu\) satisfy
- \(E\lvert \varepsilon \rvert \propto a \mu^b\)
- \(\log E\lvert \varepsilon \rvert \approx \log c + b \log \mu\)
Thus \(b\) can be estimated from spread-level plot
Call:
lm(formula = log(abs(rstudent(fm))) ~ log(fitted(fm)))
Coefficients:
(Intercept) log(fitted(fm))
-3.284 0.948
- Suggested power transform \(Y^{(1-b)} \approx Y^{0.05} \approx \log Y\)
Residuals vs fitted values (after transforming)
fm <- lm(log(wages) ~ education + age + sex, data = SLID)
xyplot(rstudent(fm) ~ fitted(fm), type = c("p", "smooth"), grid = TRUE,
col.line = "black", abline = list(h = 0, col = "grey50"))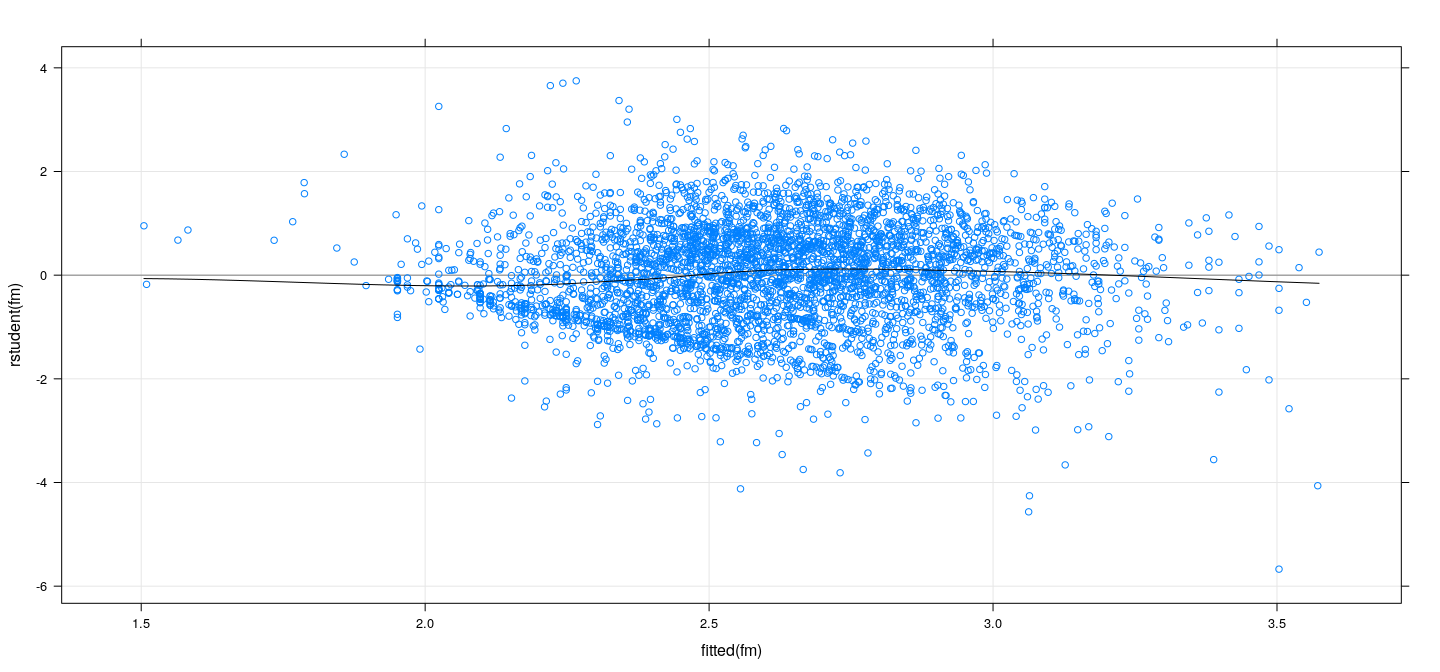
Residuals vs fitted values (after transforming)
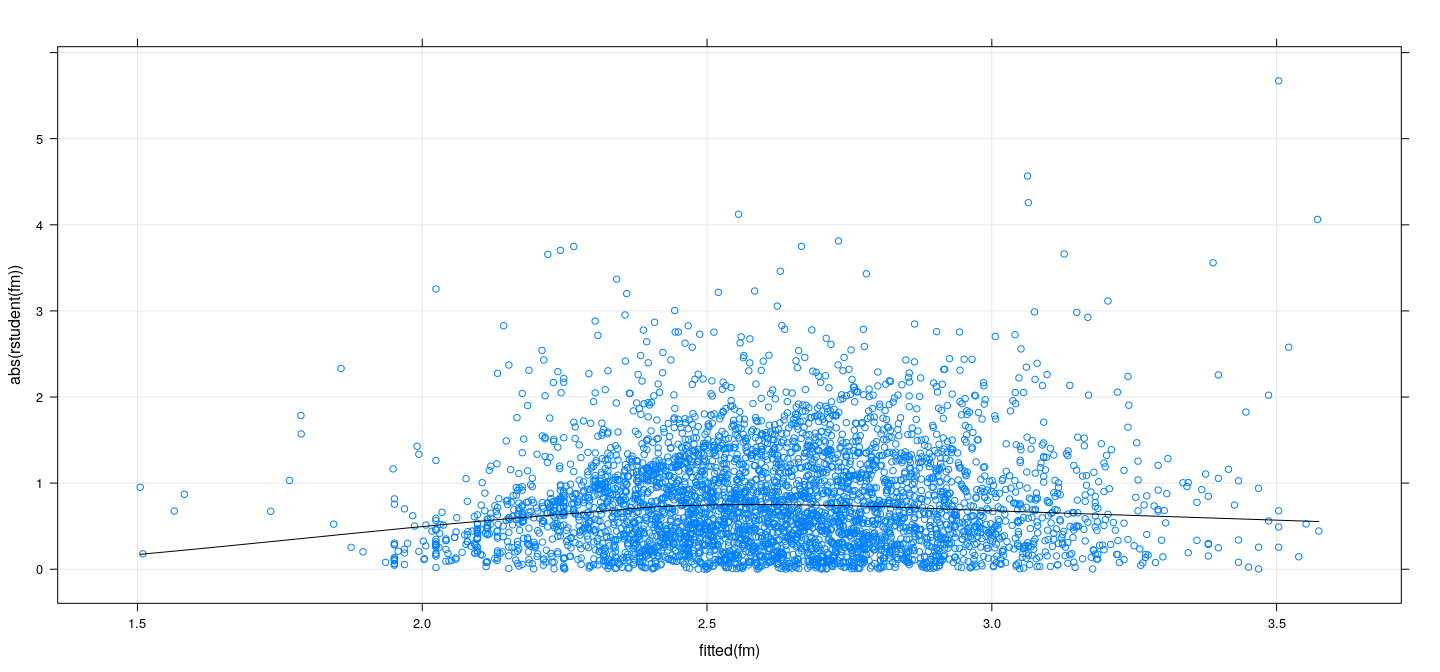
Spread-level plot (after transforming)
xyplot(abs(rstudent(fm)) ~ fitted(fm), type = c("p", "r", "smooth"), grid = TRUE,
col.line = "black", scales = list(log = TRUE, equispaced.log = FALSE))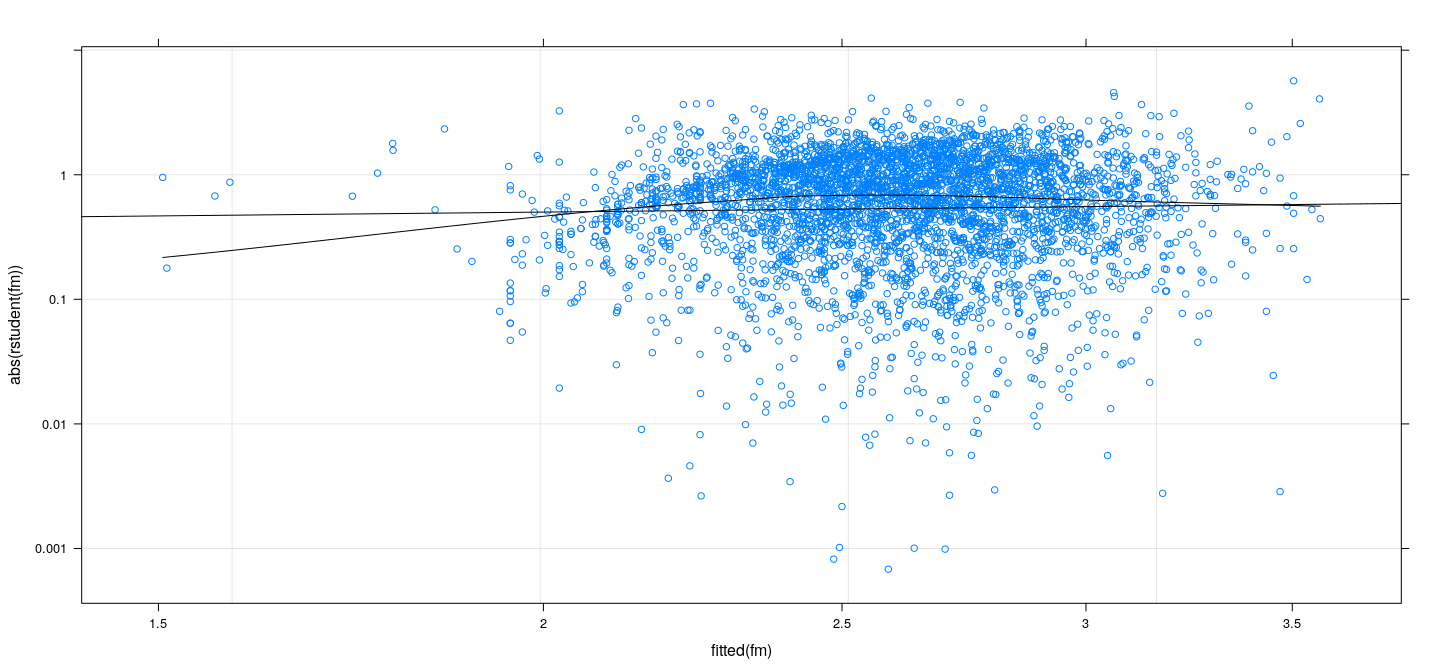
Residuals vs covariates
fm <- lm(log(wages) ~ education + age + sex, data = SLID)
xyplot(abs(rstudent(fm)) ~ education + age, data = SLID, type = c("p", "smooth"),
grid = TRUE, col.line = "black", outer = TRUE, xlab = "Covariate",
scales = list(x = "free"))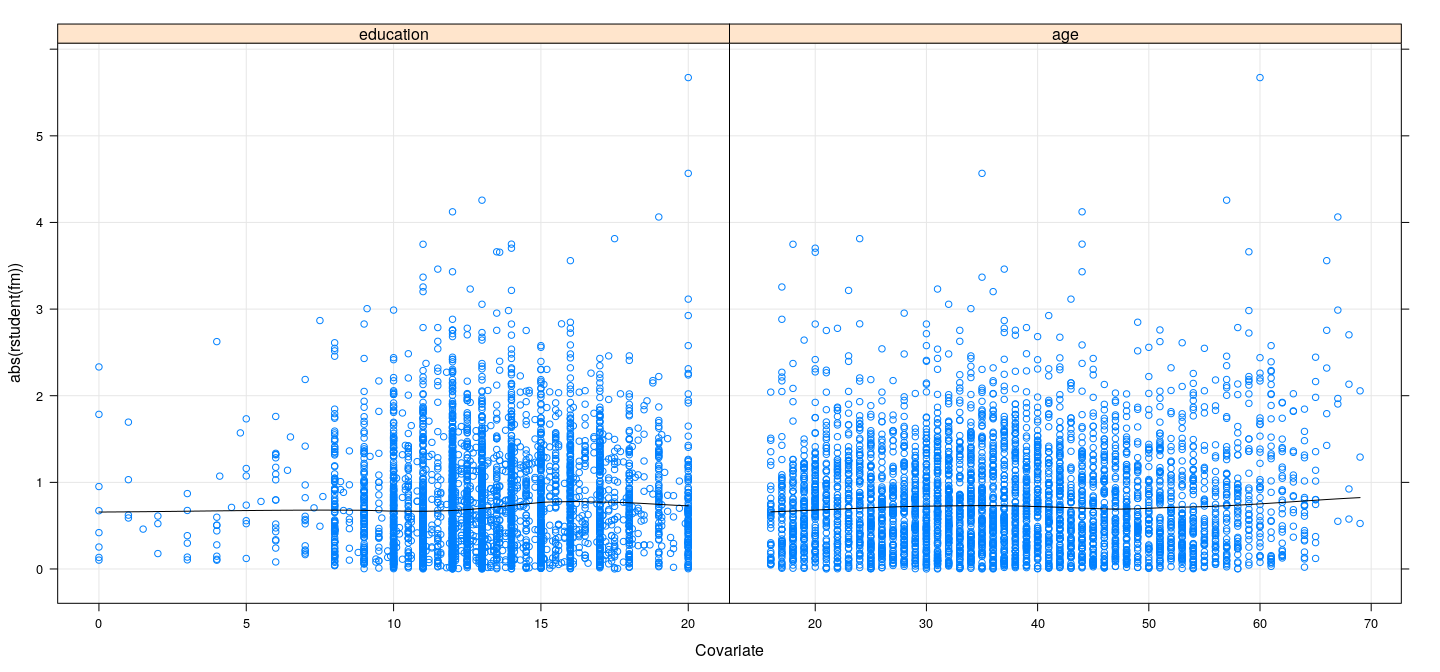
Weighted least-squares estimation
Suppose we can find known weights \(w_i\) such that \(E(y_i | \mathbf{x}_i) = \mathbf{x}_i^T \mathbf{\beta}\) and \(V(y_i | \mathbf{x}_i) = \sigma^2 / w_i^2\)
Let \(\mathbf{W}\) be a diagonal matrix with entries \(w_i^2\) and \(\mathbf{\Sigma} = \sigma^2 \mathbf{W}^{-1}\). Then
\[ \mathbf{y} \sim N( \mathbf{X} \mathbf{\beta}, \mathbf{\Sigma} ) \]
- The likelihood function is given by
Weighted least-squares estimation
- Maximum likelihood estimators are easily seen (exercise) to be given by
\[ \hat{\mathbf{\beta}} = (\mathbf{X}^T \mathbf{W} \mathbf{X})^{-1} \mathbf{X}^T \mathbf{W} \mathbf{y}\,,\quad \hat{\sigma}^2 = \frac1{n} \sum w_i^2 (y_i - \mathbf{x}_i^T \hat{\mathbf{\beta}})^2 \]
- In R,
lm()supports weighted least squares through theweightsargument
Effect of non-constant variance on OLS estimates
Let \(E(\mathbf{y}) = \mathbf{X} \beta\) and \(V(\mathbf{y}) = \mathbf{\Sigma} = diag\{ \sigma_1^2, \dotsc, \sigma_n^2 \}\)
Suppose we ignore non-constant variance and estimate \(\beta\) using OLS.
\(\hat\beta\) is still unbiased:
\[E(\hat\beta) = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T E(\mathbf{y}) = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{X} \beta = \beta\]
- Variance is given by
\[V(\hat\beta) = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{\Sigma} \mathbf{X} (\mathbf{X}^T\mathbf{X})^{-1}\]
- For a linear function
\[V(\ell^T \hat\beta) = \ell^T (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{\Sigma} \mathbf{X} (\mathbf{X}^T\mathbf{X})^{-1} \ell\]
- WLS may not be worth the effort if more or less same as OLS standard error
Detecting need for addressing non-constant variance
How can we quickly assess need for WLS?
Suppose we don’t know structural form of \(\mathbf{\Sigma}\) (e.g., which covariates affect variance)
We still know that \(E(\varepsilon_i^2) = \sigma_i^2\)
Natural estimate of \(\sigma_i^2\) after fitting OLS model: \(e_i^2\) or \(e_{i(-i)}^2\), giving \(\hat{\mathbf{\Sigma}}\)
This gives White’s “sandwich estimator”
\[\hat{V}(\hat\beta) = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \hat{\mathbf{\Sigma}} \mathbf{X} (\mathbf{X}^T\mathbf{X})^{-1}\]
White (1980) shows that this is consistent with \(\hat{\sigma}_i^2 = e_i^2\)
Long and Erwin (2000) show that \(\hat{\sigma}_i^2 = e_{i(-i)}^2\) performs better in small samples
How does this help?
We have two alternative estimates of \(V(\hat\beta)\): the OLS and the sandwich estimator
Can obtain corresponding standard errors for \(\ell^T \hat{\beta}\) (in particular for \(t\)-tests for \(\beta_j\)-s)
General strategy:
- If the standard errors using the two methods are substantially similar, OLS is sufficient
- Otherwise, need to address non-constant variance
- This does not suggest any particular remedy: usual approach is to try transformations
How does this help?
- Example:
SLIDdata
library(car) # for hccm
fm <- lm(log(wages) ~ education + age + sex, data = SLID)
summary(fm) # Q: does the standard errors of estimated coefficients change?
Call:
lm(formula = log(wages) ~ education + age + sex, data = SLID)
Residuals:
Min 1Q Median 3Q Max
-2.36252 -0.27716 0.01428 0.28625 1.56588
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.1168632 0.0385480 28.97 <2e-16 ***
education 0.0552139 0.0021891 25.22 <2e-16 ***
age 0.0176334 0.0005476 32.20 <2e-16 ***
sexMale 0.2244032 0.0132238 16.97 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4187 on 4010 degrees of freedom
Multiple R-squared: 0.3094, Adjusted R-squared: 0.3089
F-statistic: 598.9 on 3 and 4010 DF, p-value: < 2.2e-16How does this help?
- Example:
SLIDdata
(Intercept) education age sexMale
(Intercept) 1.485945e-03 -6.903578e-05 -1.278690e-05 -9.428603e-05
education -6.903578e-05 4.792018e-06 1.275037e-07 7.454834e-07
age -1.278690e-05 1.275037e-07 2.999080e-07 -7.403851e-08
sexMale -9.428603e-05 7.454834e-07 -7.403851e-08 1.748681e-04 (Intercept) education age sexMale
0.0385479539 0.0021890678 0.0005476385 0.0132237691 How does this help?
- Example:
SLIDdata
(Intercept) education age sexMale
(Intercept) 1.493908e-03 -7.018477e-05 -1.374008e-05 -7.108659e-05
education -7.018477e-05 4.946819e-06 1.370821e-07 6.523566e-07
age -1.374008e-05 1.370821e-07 3.420460e-07 -7.115594e-07
sexMale -7.108659e-05 6.523566e-07 -7.115594e-07 1.750330e-04(Intercept) education age sexMale
0.038651104 0.002224144 0.000584847 0.013230005 How does this help?
- Example:
SLIDdata
(Intercept) education age sexMale
(Intercept) 1.499263e-03 -7.045519e-05 -1.378453e-05 -7.136218e-05
education -7.045519e-05 4.964996e-06 1.377771e-07 6.614334e-07
age -1.378453e-05 1.377771e-07 3.430706e-07 -7.121512e-07
sexMale -7.136218e-05 6.614334e-07 -7.121512e-07 1.753998e-04 (Intercept) education age sexMale
0.0387203216 0.0022282270 0.0005857223 0.0132438591 Formal tests for nonconstant variance
- Model \(\sigma_i\)-s are not constant, but have the form
\[ \sigma_i^2 = V(\varepsilon_i) = g(\gamma_0 + \gamma_1 Z_{i1} + \cdots + \gamma_p Z_{ip}) \]
Here \(Z_{ij}\)-s are known (possibly same as \(X_{ij}\)-s)
In other words, variance is a function of a linear combination of known covariates
Null hypothesis: \(\gamma_1 = \cdots = \gamma_p = 0\)
Can be “tested” using an auxiliary regression with “response”
\[ u_i = \frac{e_i^2}{\frac{1}{n}\sum_k e_k^2} = \frac{e_i^2}{\hat{\sigma}^2_{MLE}} \]
Formal tests for nonconstant variance
- Breusch-Pagan test: Regress \(u_i\)-s on \(Z_{ij}\)-s:
\[ u_i = \eta_0 + \eta_1 Z_{i1} + \cdots + \eta_p Z_{ip} + \omega_i \]
- Test statistic (with \(\hat{u}_i\) fitted values from the regression):
\[ S_0^2 = \frac{1}{2} \sum_i (\hat{u}_i - \bar{u})^2 \]
Under \(H_0\), \(S_0^2\) has an asymptotic \(\chi^2\) distribution with \(p\) degrees of freedom (Breusch and Pagan, 1979)
Choice of \(Z_{ij}\)-s depends on suspected pattern of heteroscedasticity; could be all covariates
Formal tests for nonconstant variance
- Special case (Cook and Weisberg, 1983): more specific form of \(\sigma_i^2\)
\[ \sigma_i^2 = \eta_0 + \eta_1 (\mathbf{x}_i^T \beta) + \omega_i \]
- Test by fitting the model
\[ u_i = \eta_0 + \eta_1 \hat{y}_i + \omega_i \]
Test for \(H_0: \eta_1 = 0\) (one degree of freedom)
More powerful test when heteroscedasticity follows this pattern
Formal tests for nonconstant variance: example
SLIDdata,wagesas response
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 310.6546 Df = 1 p = 1.572642e-69 Non-constant Variance Score Test
Variance formula: ~ education + age
Chisquare = 297.4689 Df = 2 p = 2.54358e-65 Formal tests for nonconstant variance: example
SLIDdata,log(wages)as response
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 28.09925 Df = 1 p = 1.152505e-07 Non-constant Variance Score Test
Variance formula: ~ education + age + sex
Chisquare = 38.44827 Df = 3 p = 2.271575e-08 Nonlinearity
Non-linearity means the modeled expectation \(E(\mathbf{y}) = \mathbf{X} \beta\) is not adequate
In multiple regression, with many predictors, this may be difficult to detect
Usual strategy: look for indicative patterns in residuals for one predictor at a time
Simplest option is to plot residuals against predictor
But this may not be able to distinguish between monotone and non-monotone relationships
Important to do so because monotone nonlinearity can often be corrected using transformation
Residual vs covariate: example
n <- 100; x <- runif(n)
y1 <- x^2 + rnorm(n, sd = 0.1)
y2 <- 1 - x + x^2 + rnorm(n, sd = 0.1)
fm1 <- lm(y1 ~ x)
fm2 <- lm(y2 ~ x)
xyplot(residuals(fm1) + residuals(fm2) ~ x, type = c("p", "smooth"), outer = TRUE, ylab = "Residuals")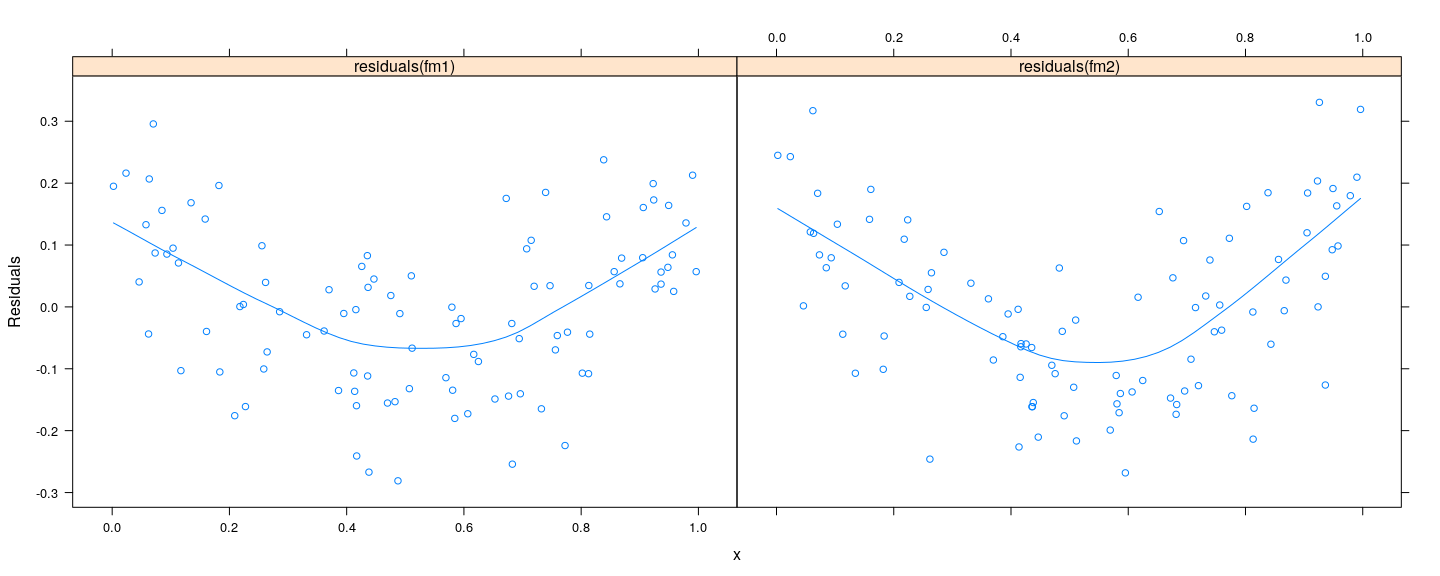
Residual vs covariate: example
- Similar residual plots, but nature of models are different
- First model can be made linear by transformation (true model: \(y = \alpha + \beta x^2 + \varepsilon\))
- Second model is truly quadratic ((true model: \(y = \alpha + \beta x + \gamma x^2 + \varepsilon\))
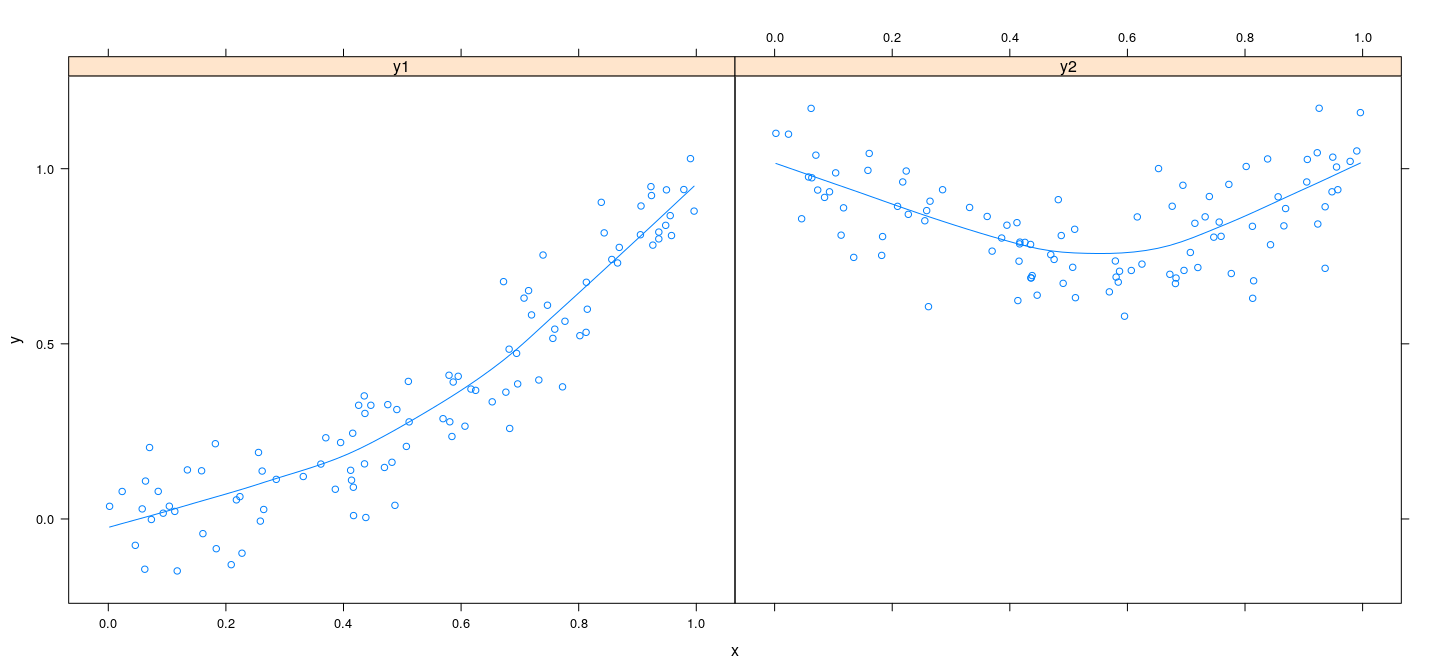
Component plus residual plots
X-axis: \(j\)-th covariate (more accurately, \(j\)-th column of \(\mathbf{X}\))
Y-axis: partial residuals of \(\mathbf{y}\) on \(\mathbf{X}\) excluding \(j\)-th column:
\[e_i^{(-j)} = e_i + \hat{\beta}_j X_{ij}\]
In other words, add back the contribution of the \(j\)-th covariate
Similar to added-variable plots, but covariate is not adjusted
Add non-parametric smoother to detect non-linearity
Component plus residual plots: example
fm <- lm(log(wages) ~ education + age + sex, data = SLID)
crPlots(fm, ~ education + age, layout = c(1, 2))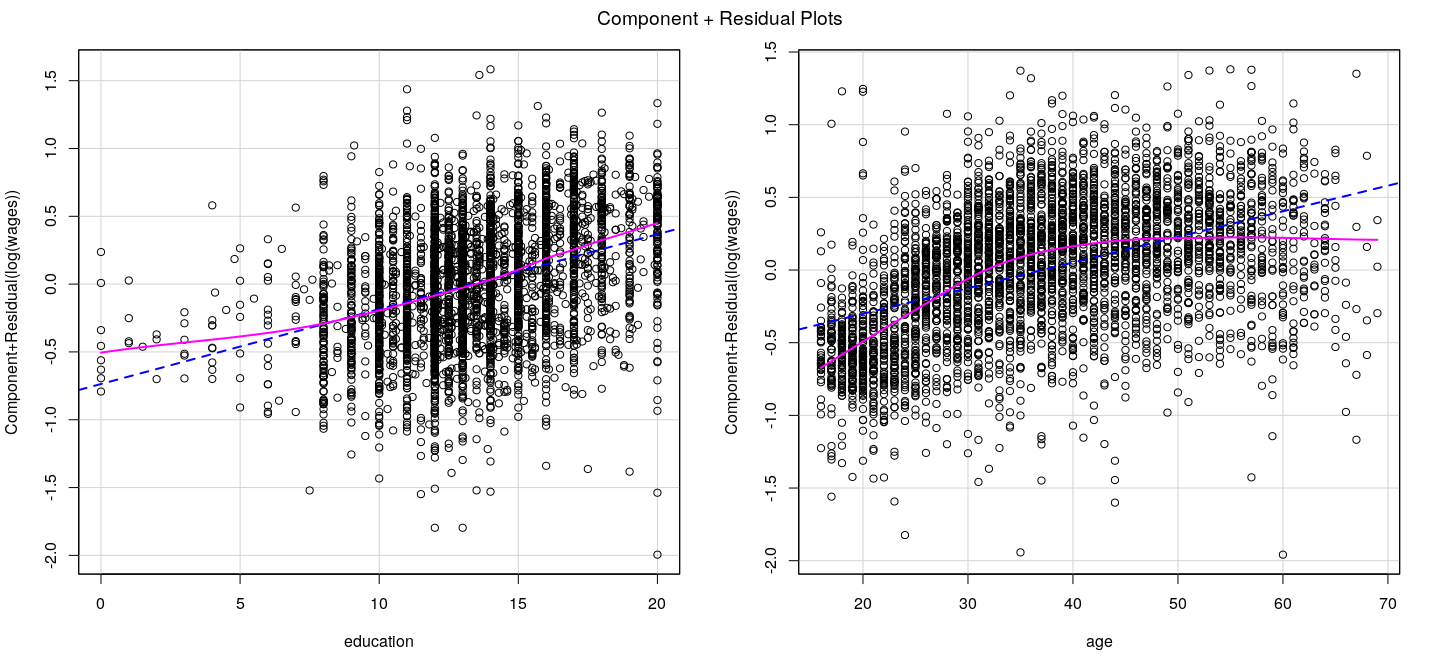
Component plus residual plots: example
fm <- lm(log(wages) ~ I(education^2) + sqrt(age) + sex, data = SLID) # transform both age and education
crPlots(fm, ~ . - sex, layout = c(1, 2)) # all terms excluding sex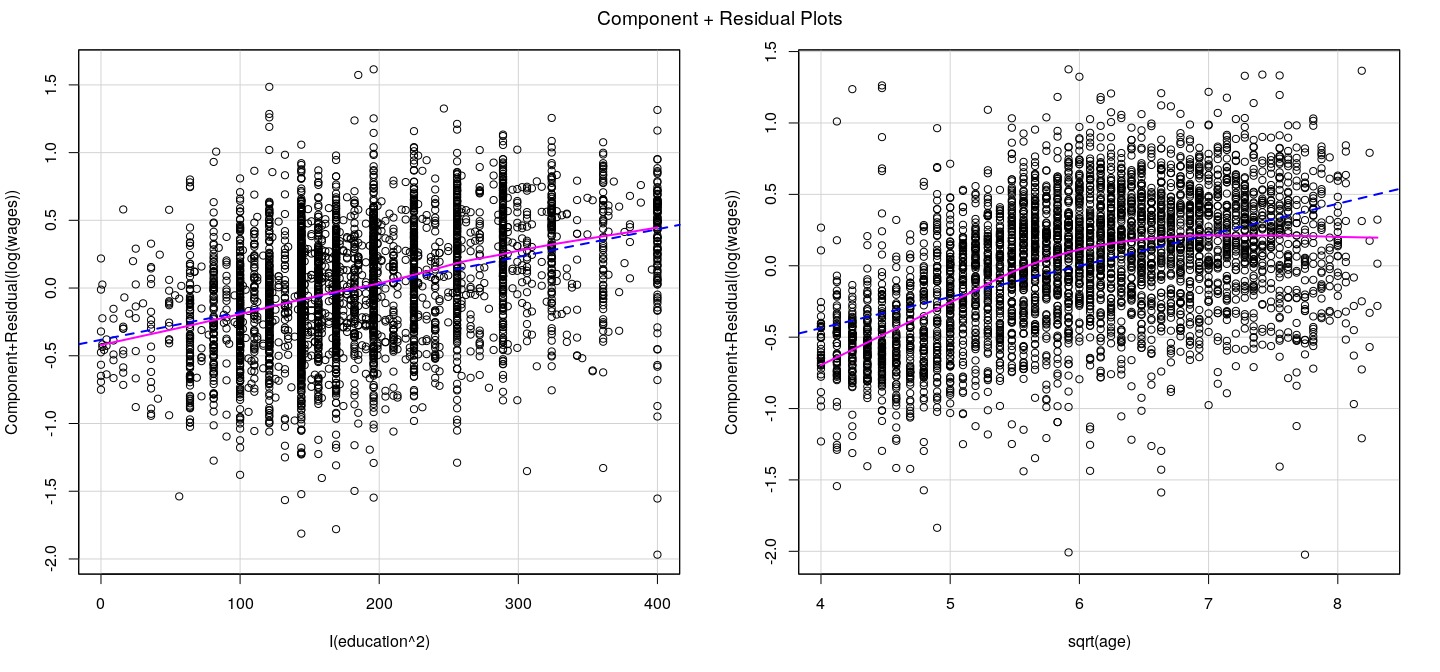
Component plus residual plots: example
fm <- lm(log(wages) ~ I(education^2) + poly(age, 2) + sex, data = SLID) # quadratic age
crPlots(fm, ~ . - sex, layout = c(1, 2)) # multicolumn terms are handled gracefully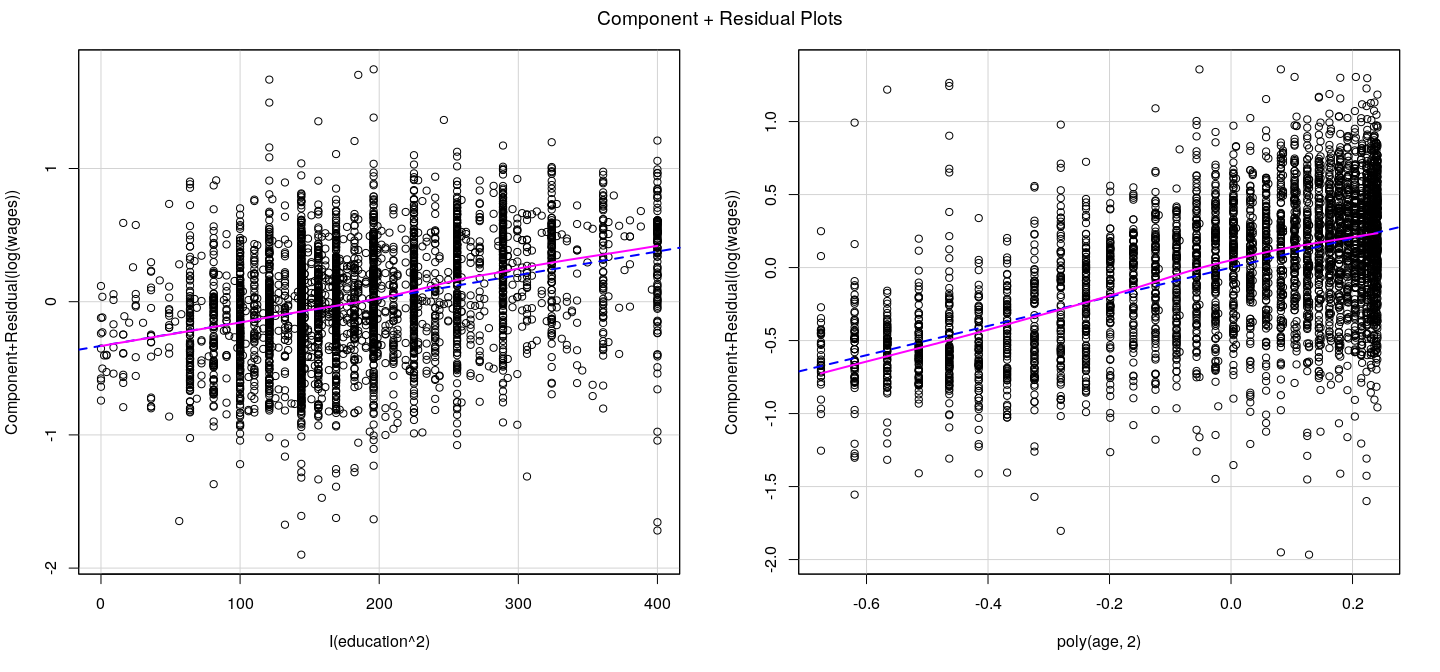
Component plus residual plots: caveats
Higher dimensional relationships in multiple regression models can be complicated
Component plus residual plots are two dimensional projections
May not always work: in particular, if covariates are non-linearly related
See Mallows (1986) for an approach that accounts for quadratic relationships with other covariates
See Cook (1993) for a more general approach (CERES plots)
Nonlinearity for discrete predictors
As discussed earlier, discrete covariates (few unique values, many ties) allow us to fit “pure error” models
Pure error models represent a model with no restrictions on the mean function \(f(x) = E(Y | X = x)\)
Can be used to test “lack of fit” for any more specific form of \(f(x)\)
- Example:
GSSvocab(28867 observations)- Response:
vocab(Number of words out of 10 correct on a vocabulary test) - Predictors:
age(in years) andeduc(years of education)
- Response:
Example: GSSvocab data
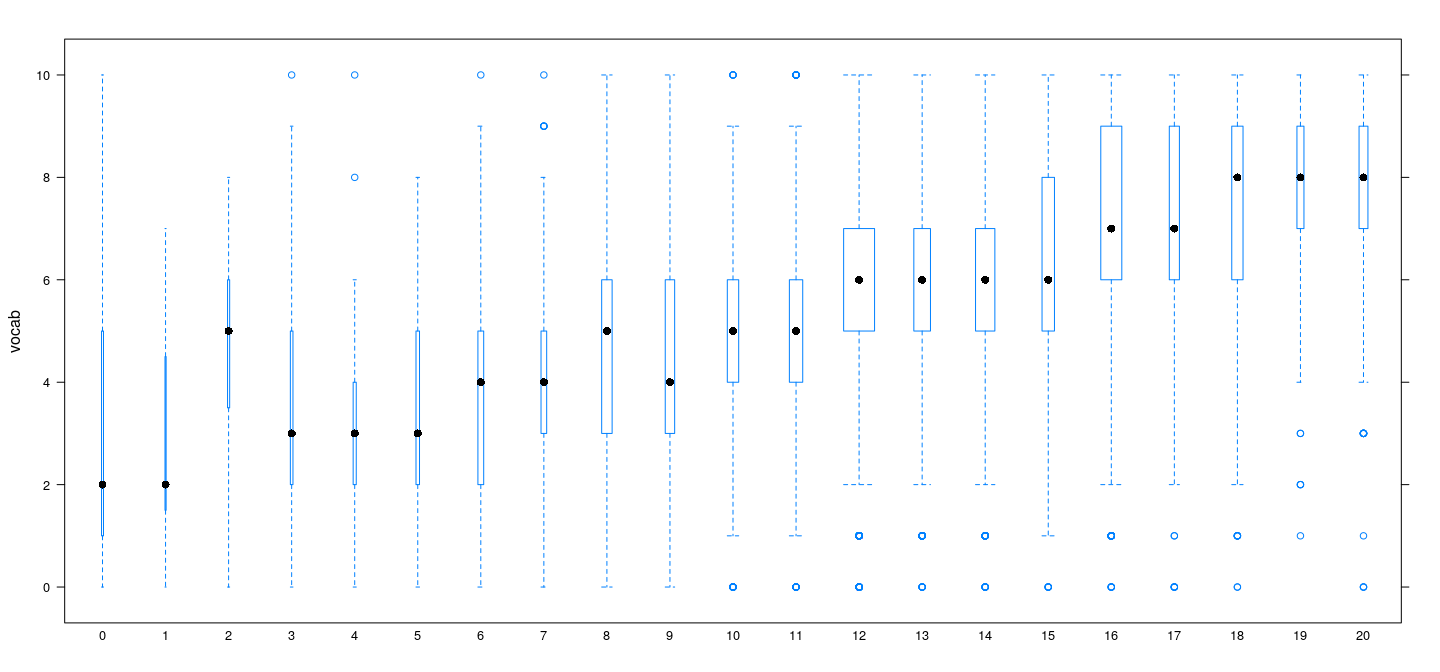
Example: GSSvocab data
fm1 <- lm(vocab ~ educ, GSSvocab) # linear regression model
mean.vocab <- aggregate(vocab ~ educ, GSSvocab, mean)
xyplot(vocab ~ educ, mean.vocab, grid = TRUE, pch = 16, type = "o") + layer(panel.abline(fm1))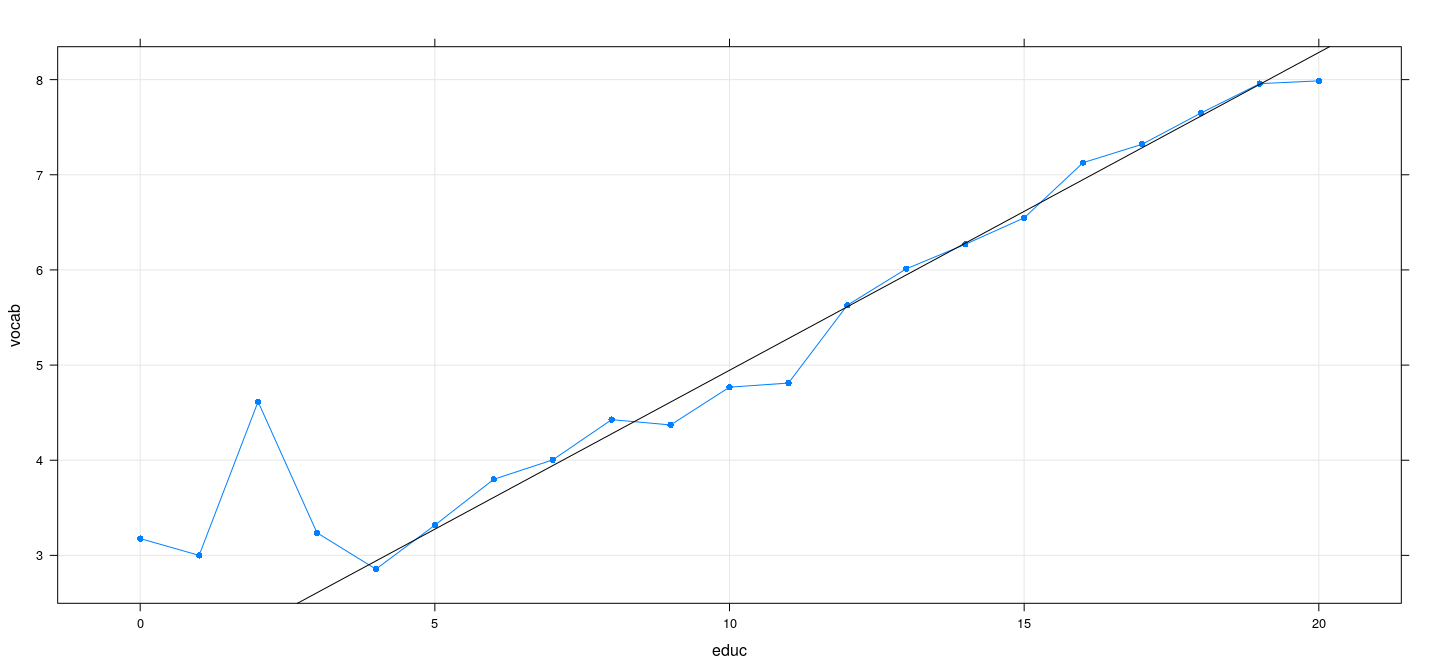
Example: GSSvocab data
Analysis of Variance Table
Model 1: vocab ~ educ
Model 2: vocab ~ factor(educ)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 27471 93895
2 27452 92906 19 989.32 15.386 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Example: GSSvocab data
- Even though there is significant lack of fit, the improvement is marginal
[1] 0.2283162[1] 0.236447
- This is a common theme
- Statistical tests are more sensitive for large \(n\)
- Statistical significance does not necessarily mean the difference (effect) is important in practice
Example: SLID data
- We can do similar tests for multiple regression models
fm1 <- lm(log(wages) ~ I(education^2) + poly(age, 2) + sex, data = SLID)
fm2 <- lm(log(wages) ~ factor(education) + poly(age, 2) + sex, data = SLID)
fm3 <- lm(log(wages) ~ I(education^2) + factor(age) + sex, data = SLID)
fm4 <- lm(log(wages) ~ factor(education) + factor(age) + sex, data = SLID)- \(R^2\) does not improve substantially
$fm1
[1] 0.384718
$fm2
[1] 0.4086884
$fm3
[1] 0.3996565
$fm4
[1] 0.423225Example: SLID data
- Formal lack of fit tests
Analysis of Variance Table
Model 1: log(wages) ~ I(education^2) + poly(age, 2) + sex
Model 2: log(wages) ~ factor(education) + factor(age) + sex
Res.Df RSS Df Sum of Sq F Pr(>F)
1 4009 626.42
2 3834 587.21 175 39.204 1.4627 9.9e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Example: SLID data
Analysis of Variance Table
Model 1: log(wages) ~ factor(education) + poly(age, 2) + sex
Model 2: log(wages) ~ factor(education) + factor(age) + sex
Res.Df RSS Df Sum of Sq F Pr(>F)
1 3885 602.01
2 3834 587.21 51 14.8 1.8947 0.0001394 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Analysis of Variance Table
Model 1: log(wages) ~ I(education^2) + factor(age) + sex
Model 2: log(wages) ~ factor(education) + factor(age) + sex
Res.Df RSS Df Sum of Sq F Pr(>F)
1 3958 611.21
2 3834 587.21 124 23.995 1.2634 0.02743 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Using pure error models to test for non-constant variance
- With discrete predictors, constant variance means within-group sample variances should be similar
\[ S_j^2 = \frac{1}{n_j-1} \sum_{i=1}^{n_j} (y_{ij} - \bar{y}_j)^2, j = 1, \dotsc, k \]
- Define the pooled variance
\[ S_p^2 = \frac{1}{n-k} \sum_{j=1}^k (n_j - 1) S_j^2, \text{ where } n = \sum_{j=1}^k n_j \]
- Then Bartlett’s test statistic is (an adjustment of the likelihood ratio test statistic)
\[ T = \frac{(n-k) \log S_p^2 - \sum_{j=1}^k (n_j-1) \log S_j^2 }{1 + \frac{1}{3(k-1)} (\sum_{j=1}^k \frac{1}{n_j - 1} - \frac{1}{n-k})} \]
- Under the null distribution of constant variance, \(T\) follows a \(\chi^2\) distribution with \((k-1)\) d.f.
Using pure error models to test for non-constant variance
- Example:
GSSvocabdata
sd.vocab <- aggregate(vocab ~ educ, GSSvocab, sd)
xyplot(vocab ~ educ, sd.vocab, grid = TRUE, pch = 16, type = "o")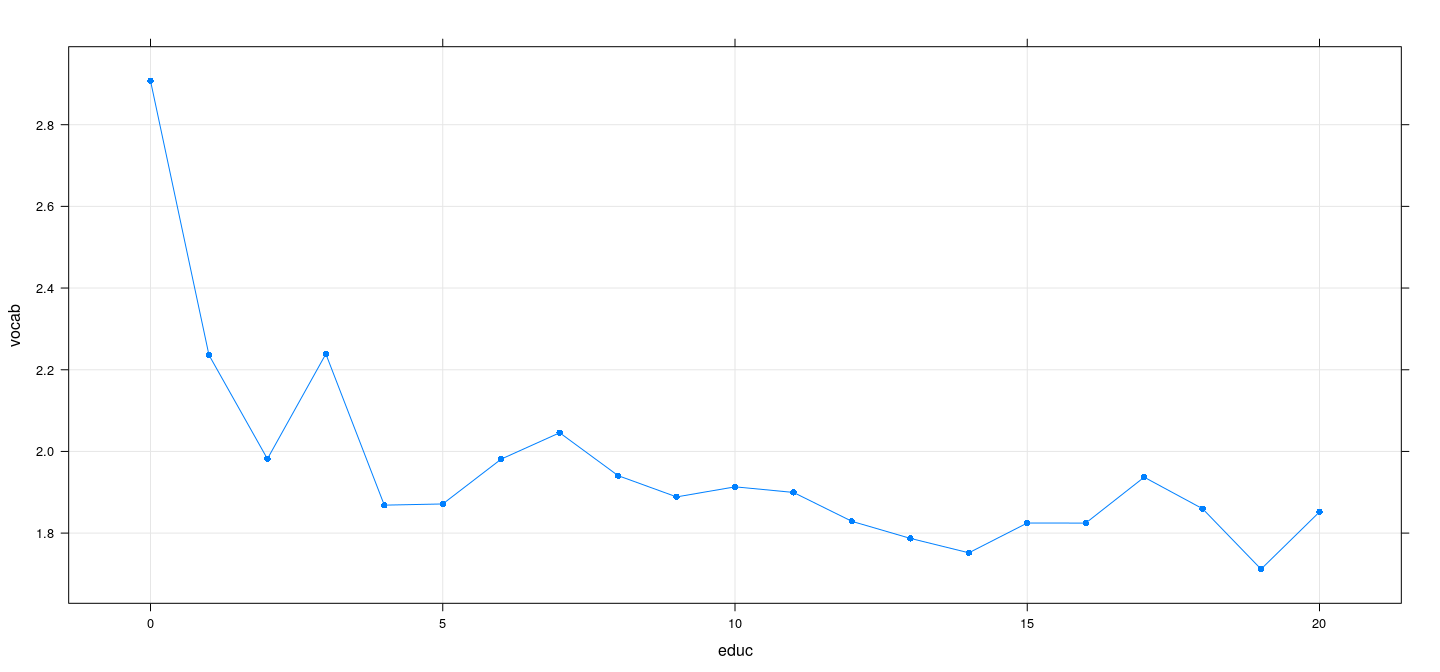
Using pure error models to test for non-constant variance
Bartlett test of homogeneity of variances
data: vocab by factor(educ)
Bartlett's K-squared = 78.606, df = 20, p-value = 6.761e-09Bartlett’s test is not robust when errors are non-normal
Levene’s test is a more robust alternative
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 20 5.3673 6.42e-14 ***
27452
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The Box-Cox transformation: a likelihood-based approach
- The Box-Cox transformation deals with non-normality, non-linearity, and non-constant variance
\[ g_\lambda(y) = \begin{cases} \frac{y^\lambda - 1}{\lambda} & \lambda \neq 0 \\ \log y & \lambda = 0 \end{cases} \]
Can we choose \(\lambda\) using a formal inference procedure?
Suppose the assumptions of the normal linear model holds for the transformed response
\[ g_\lambda(y_i) \sim N( \mathbf{x}_i^T \beta, \sigma^2), i = 1, \dotsc, n \]
- To estimate \(\lambda\) by maximizing likelihood, we need the density of the untransformed response \(\mathbf{y}\) in terms of \(\lambda\)
The Box-Cox transformation: a likelihood-based approach
- The likelihood function based on the untransformed response is
\[ \ell(\lambda, \beta, \sigma^2 \mid \mathbf{y}) = \frac{1}{(2\pi)^{n/2} \sigma^n} e^{-\frac{1}{2 \sigma^2} \lVert g_{\lambda}(\mathbf{y}) - \mathbf{X} \beta \rVert^2 } \, J(\lambda; \mathbf{y}) \]
- Here the Jacobian of the transformation is
\[ J(\lambda; \mathbf{y}) = \prod_{i=1}^n \left\lvert g_{\lambda}^{\prime}(y_i) \right\rvert, \text{ where } g_{\lambda}^{\prime}(y_i) = \frac{\mathrm{d}}{\mathrm{d} y} \left(\frac{y^\lambda - 1}{\lambda}\right) = y^{\lambda-1} \]
- This also holds for \(\lambda = 0\), as \(\frac{\mathrm{d}}{\mathrm{d} y} \log y = y^{0-1}\). So,
\[ J(\lambda; \mathbf{y}) = \prod_{i=1}^n y_i^{\lambda - 1} \]
The Box-Cox transformation: a likelihood-based approach
- For a particular choice of \(\lambda\)
- The likelihood is minimized when \(\beta\) and \(\sigma^2\) are MLEs for the model \(g_{\lambda}(\mathbf{y}) \sim N(\mathbf{X}\beta, \sigma^2 \mathbf{I})\)
- Corresponding profile log-likelihood is
\[ \log \ell(\lambda) = -\frac{n}{2} (\log 2\pi + \log \hat{\sigma}^2(\lambda) + 1) + (\lambda-1) \sum_i \log y_i \]
The global joint optimum for \((\lambda, \beta, \sigma^2)\) can be obtained by maximizing this w.r.t. \(\lambda\)
No closed-form solution, so usually solved numerically
For specific choice \(\lambda_0\), \(H_0: \lambda = \lambda_0\) can be tested using LRT (asymptotically \(\chi^2_1\))
This test can be inverted to give a confidence interval for \(\lambda\)
In practice, we choose a “simple” \(\lambda\) close to the optimum (for interpretability of the model)
The Box-Cox transformation: example
fm <- lm(wages ~ education + age + sex, data = SLID)
boxCox(fm, lambda = seq(-0.5, 0.5, 0.1), plotit = TRUE) # log is close enough to optimum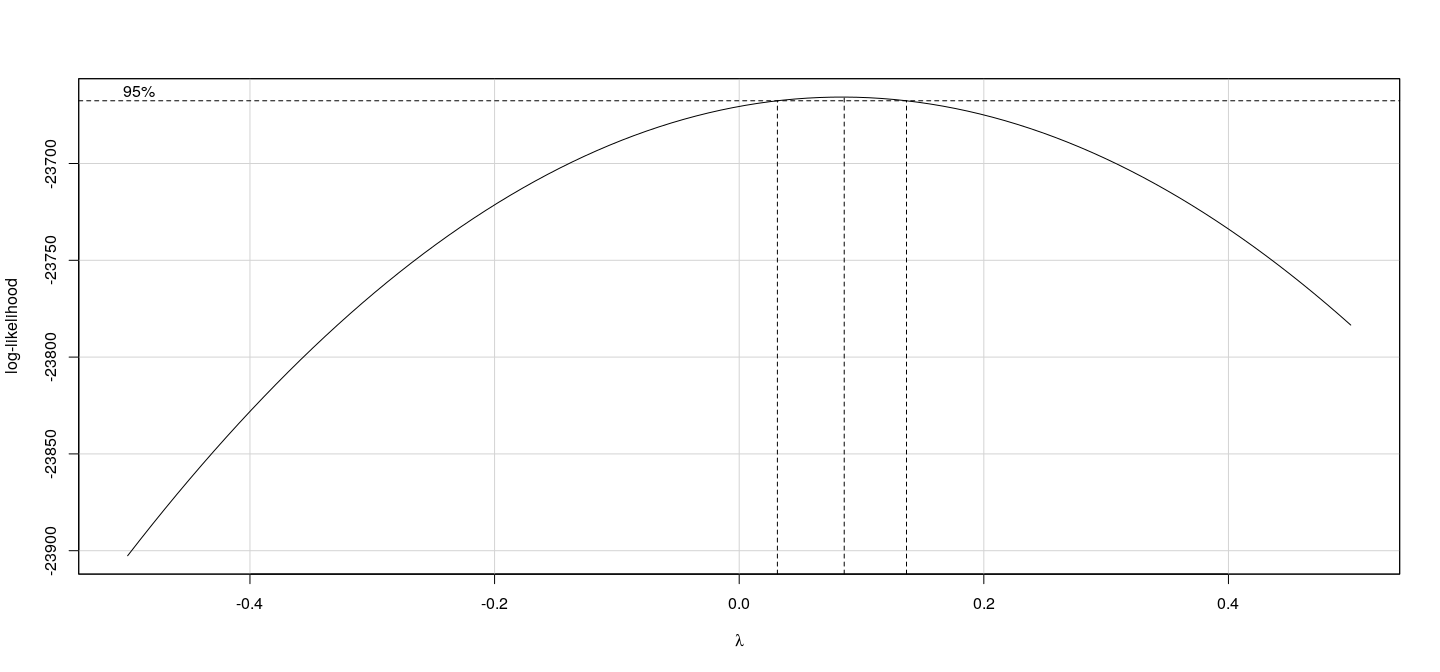
The Box-Tidwell procedure for transforming covariates
- A similar likelihood approach can be used to estimate covariate transformations. Suppose
\[ y_i = \alpha + \sum_j \beta_j X_{ij}^{\gamma_j} + \varepsilon_i,\, \varepsilon_i \sim N(0, \sigma^2) \]
Likelihood is simpler as response is not transformed, but potentially large number of parameters
No closed-form solution
Box and Tidwell (1962) suggest an iterative procedure to obtain MLEs
Linear approximation of the model:
\[ y_i = \alpha + \sum_j \beta^\prime_j X_{ij} + \delta_j X_{ij} \log X_{ij} + \varepsilon_i,\, \varepsilon_i \sim N(0, \sigma^2) \]
- This follows from the First-order Taylor series approximation
\[ x^\gamma \approx x + (\gamma-1) x \log x \]
The Box-Tidwell procedure for transforming covariates
Iterative procedure
Regress \(y_i\) on \(X_{ij}\) to obtain \(\hat{\beta}_j\)
Regress \(y_i\) on \(X_{ij}\) and \(\log X_{ij}\) to obtain \(\hat{\beta}^\prime_j\) and \(\hat{\delta}_j\)
Test \(H_0: \delta_j = 0\) to assess need for transformation
Preliminary estimate \(\tilde{\gamma}_j = 1 + \frac{\hat{\delta}_j}{\hat{\beta}_j}\) (Note: not \(\hat{\beta}^\prime_j\))
Transform \(X_{ij} \mapsto X_{ij}^{\tilde{\gamma}_j}\) and iterate until estimates stabilize
Exercise: If MLE \(\hat{\gamma}_j = 1\), model fit should give \(\hat{\delta}_j = 0\)
The Box-Tidwell procedure: example
MLE of lambda Score Statistic (z) Pr(>|z|)
I(0.01 + education) 1.8696 4.396 1.103e-05 ***
age -1.6301 -21.772 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
iterations = 9